WELCOME TO THE 3 RD ANNUAL DAMIEN HIGH

WELCOME TO THE 3 RD ANNUAL DAMIEN HIGH SCHOOL MATH COMPETITION 2012 If you have not yet registered and received a name tag, please make your way to the front of the Activity Center.

SUPER QUIZ BOWL • This is a group competition in which many problems must be solved through collaboration. • Scratch paper is available at your tables, but the final answer for each problem must be written legibly in the box on the provided answer forms. • The final solution must be true for all the given clues. • Each question is worth different amounts of

PROBLEM #1 x , y , 10 , z , 18 , … In the sequence above, the same positive integer is added to each term, starting with x, to obtain the next term in the sequence. What is the sum of the first five terms of the sequence?

PROBLEM # 1 : SOLUTION y , 10 , 14 z , 18 , … 2 x, 6 Since the same positive integer is added to each term, the distance from 10 to z must be the same as the distance from z to 18. The distance from 10 to 18 is 8, so the common distance between each term must be 4. 10 + 4 = 14 = z 10 - 4 = 6 = y So 2 + 6 + 10 + 14 + 18 = 6 -4=2=x 50

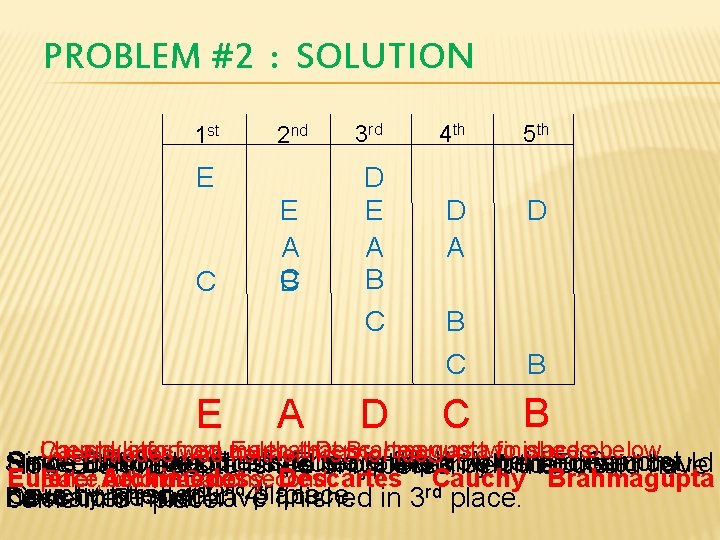
PROBLEM #2 We live in a very competitive world, as is being demonstrated here today. Cauchy is one of the most competitive people I know and was very upset when he did not earn first place in a math competition against Archimedes, Brahmagupta, Descartes, and Euler. (He’s just lucky that Newton wasn’t in the race). Cauchy informed me that Descartes finished two places below Euler, who was not second. Archimedes was neither first nor last. I heard later from Euler, that Brahmagupta finished one place behind Cauchy. Find the order that they finished in the competition.

PROBLEM #2 : SOLUTION 1 st 2 nd 3 rd 4 th 5 th E A C B D E A B D A D C B E C E A D C B informed me that Descartes was two placesone below ICauchy heard later from Euler, Brahmagupta finished Archimedes was neither first nor last. Since all of the other spots are filled, Archimedes must Brahmagupta finished one place behind Cauchy, Based off of the clues, Euler is the only person that could Descartes finished two places behind Euler, Now Brahmagupta is the only person left that could have Euler Descartes Cauchy Brahmagupta Euler, Archimedes who was not second. place behind Cauchy. th place. have 2 in Cauchy come in in 1 sthave. nd 4 place. Descartes finished in 3 rd place. comefinished in finished 5 thmust place

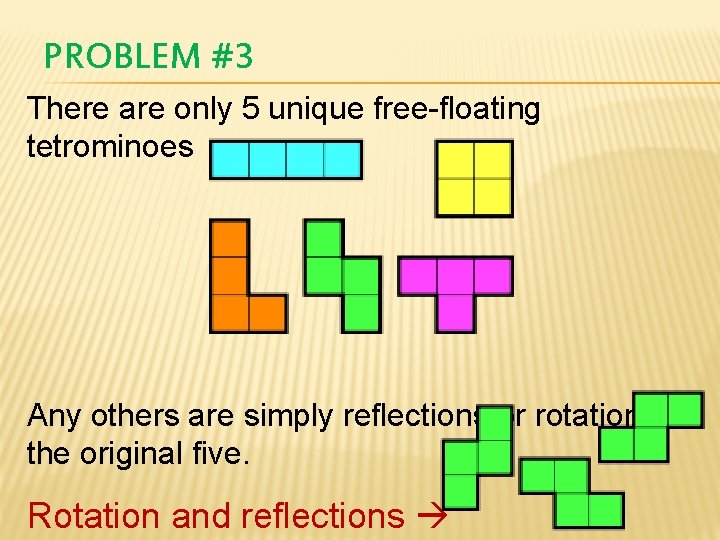
PROBLEM #3 “A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. Polyominoes are classified according to the number of cells that compose them. ” While many people would have difficulty understanding the meaning of this statement, most would be familiar with a certain type of polyomino from one of the worlds most popular

PROBLEM #3 Tetris is a game of polyominoes with 4 squares. These 4 square polynominoes are called Tetrominoes (TETRA is a Greek prefix for 4). Each piece in a traditional game of Tetris is made up of 4 adjacent squares, arranged in 5 different ways.

PROBLEM #3 There are only 5 unique free-floating tetrominoes Any others are simply reflections or rotations of the original five. Rotation and reflections

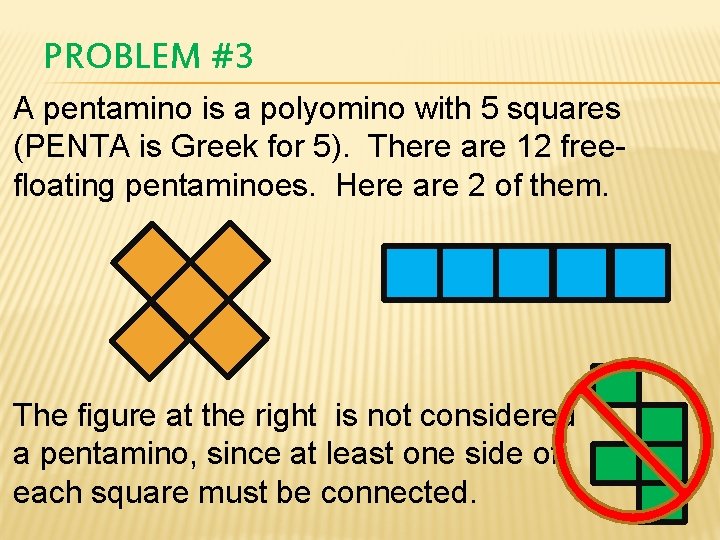
PROBLEM #3 A pentamino is a polyomino with 5 squares (PENTA is Greek for 5). There are 12 freefloating pentaminoes. Here are 2 of them. The figure at the right is not considered a pentamino, since at least one side of each square must be connected.

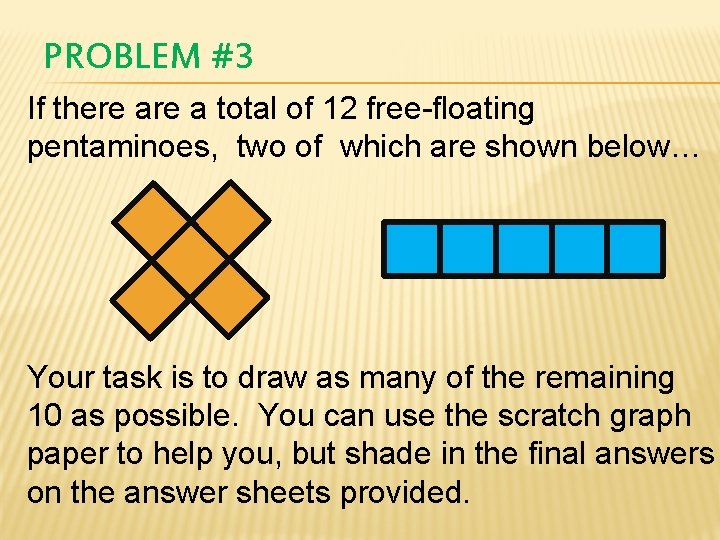
PROBLEM #3 If there a total of 12 free-floating pentaminoes, two of which are shown below… Your task is to draw as many of the remaining 10 as possible. You can use the scratch graph paper to help you, but shade in the final answers on the answer sheets provided.

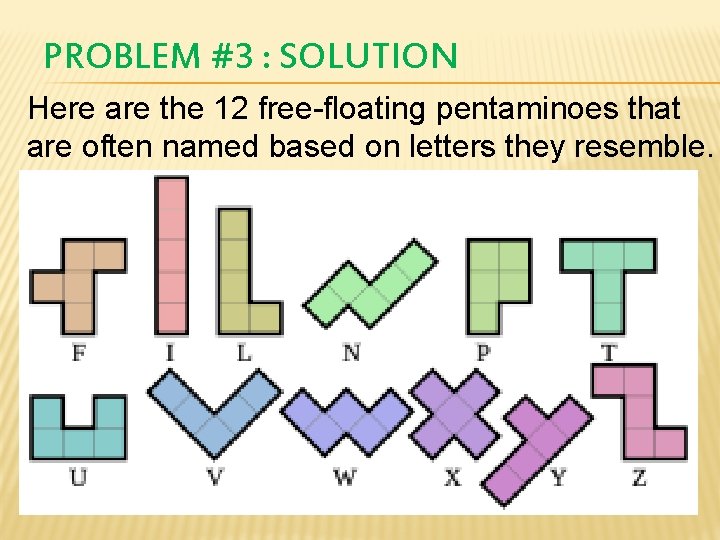
PROBLEM #3 : SOLUTION Here are the 12 free-floating pentaminoes that are often named based on letters they resemble.

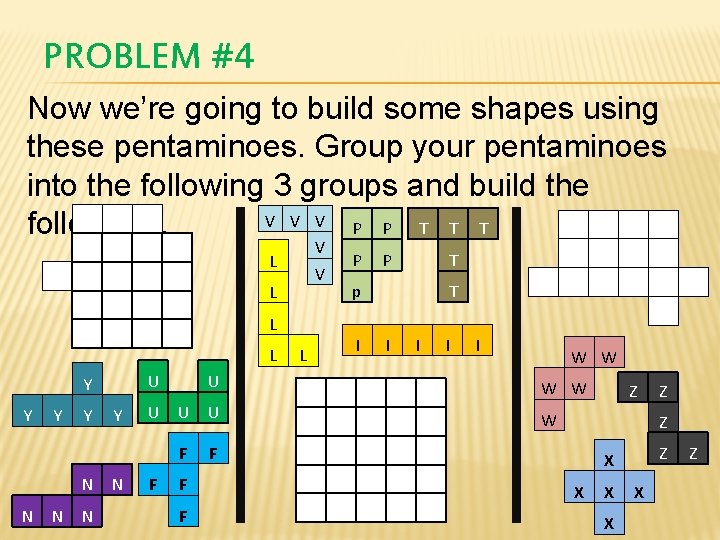
PROBLEM #4 Now we’re going to build some shapes using these pentaminoes. Group your pentaminoes into the following 3 groups and build the V V V following. . P P T T T V V L L U Y Y N N Y N U F L P P T p I T I I W W U U W F F Z Z X X X Z

PROBLEM #4 : SOLUTION Here are 3 possible solutions, though these are not necessarily the only solutions. N N N L T V V V Z Z W W F F N N L T T T V Z W W X F F U U U L T P P V Z Z W X X X F U Y U L L P P P Y Y I I I X

PROBLEM #5 Using the numerals 1, 9, 9 and 6 (IN THAT ORDER), along with parentheses and the mathematical operations of + , - , x , , create the following numbers : 0 , 1 , 3 , 4 , 6 , 7 All the numerals must be used in the given order (each just once) and without turning upside down. You may combine two numerals together, like

PROBLEM #5 : SOLUTION

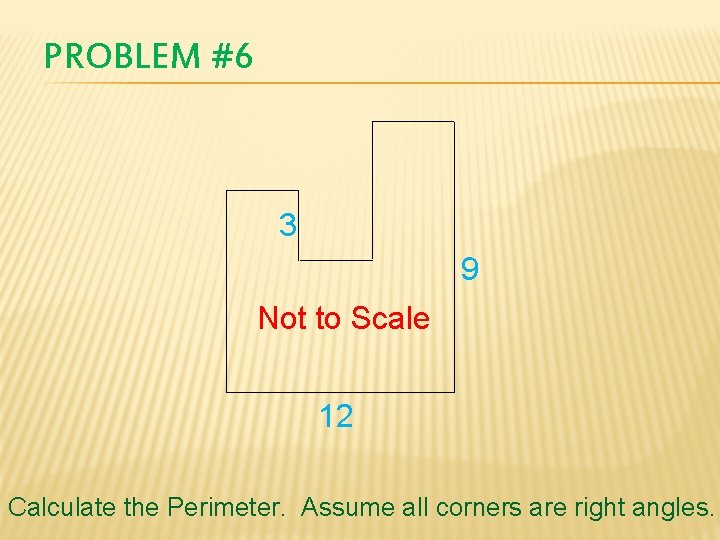
PROBLEM #6 3 9 Not to Scale 12 Calculate the Perimeter. Assume all corners are right angles.

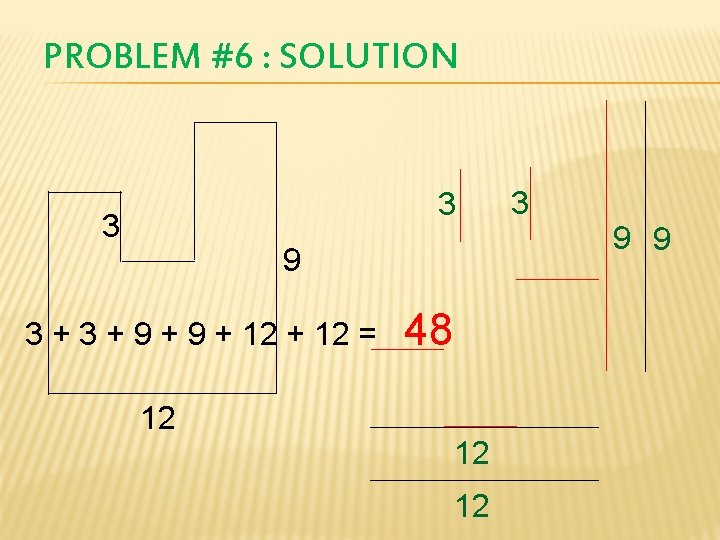
PROBLEM #6 : SOLUTION 3 3 9 3 + 9 + 12 = 12 48 12 12 3 9 9

PROBLEM #7 How many positive three-digit numbers are there such that each digit is an odd number less than 8, and none of the digits can be repeated? Note : You do not NEED to list the specific numbers.

PROBLEM #7 : SOLUTION : 1 st 2 nd 3 rd Choices : 4 3 2 Digits The 1 st digit has 4 possibilities. The 2 nd digit only has 3 possibilities, since it cannot be the same as the 1 st digit. The 3 rd digit only has 2 possibilities, since it cannot be the same as the 1 st or 2 nd digits. Since each digit must Digit of 1 : be odd, our choices are 135 , 137 , 153 , 157 , 173 , 175 either 1, 3, 5, 7, or 9. 1 st Digit of 3 : 315 , However, 317 , 351 , each 357 , 371 digit, 375 must be less than 8, Digit of 5 : so we can only choose 513 , 517 , 531 , 537 , 571 , 573 1, 3, 5, or 7. 1 st Digit of 7 : 713 , 715 , 731 , 735 , 751 , 753 There are 4 x 3 x 2 = 24 Since digits cannot repeat, once it’s used, it different numbers cannot be used again.

PROBLEM #8 • Assume Damien High School has 1200 students. • Each student at Damien takes 5 classes. • Each class at Damien has 30 students and 1 teacher. • Every teacher at Damien teaches 4 classes a day (They each have one free period for planning). • Every student at Damien has to take a class during each of the five periods. How many teachers are there at Damien High School?

PROBLEM #8 : SOLUTION Since there are 1200 students and 30 students per class, then there are 1200 ÷ 30 = 40 classes period. Since there are 5 periods per day, then there a total of 5 × 40 = 200 classes per day. Since each teacher teaches 4 classes per day, then there a total of 200 ÷ 4 = 50 teachers at Damien High.

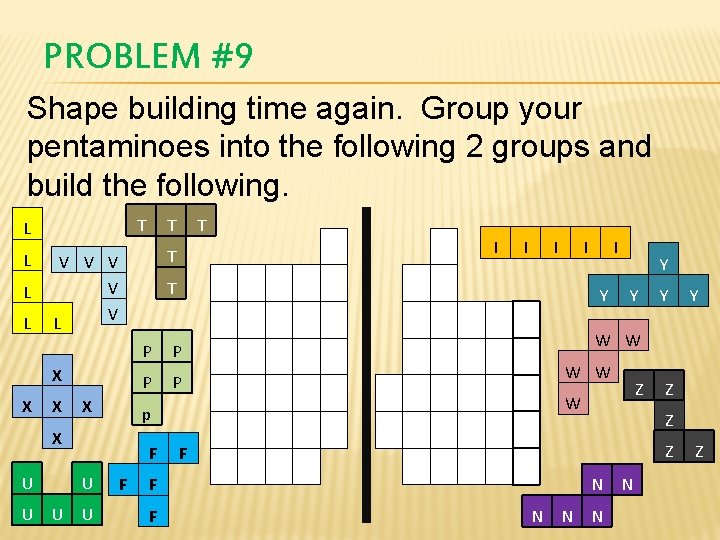
PROBLEM #9 Shape building time again. Group your pentaminoes into the following 2 groups and build the following. T L L X X U U U I I I P P P Y W W Z W Y Y Z Z Z F F F Y W W p F I Y P F U I T X U T T V V V L X X T N N N Z

PROBLEM #9 : SOLUTION Here are 2 possible solutions, though these are not the only solutions. T T N L L T T N N L V V V T N Z Z Y I L V U U U N Z Y Y I L V U X U W Z Z F Y I P P X X W W F F Y I P P P X W W F F I X

TIE BREAKER !!!

THANK YOU FOR COMING TO THE 3 RD ANNUAL DAMIEN HIGH SCHOOL MATH COMPETITION See you next year!

TIEBREAKER #1 If John gives Paul one apple, they will have the same number of apples. If Paul gives John one apple, John will have twice as many apples as Paul does. How many apples does each have?

TIEBREAKER #1 : SOLUTION If we let J = the # of apples that John has and we let P = the # of apples that Paul has, then we can rewrite the statements as : J = P +2 J – 1 = P +1 J + 1 = 2(P - 1) (P +2) + 1 = 2(P– 1) P + 3 = 2 P - 2 P = 5 apples Since J = P + 2 , then J = 7 apples.

TIEBREAKER #2 An eccentric professor used a unique way to measure time for a test lasting 15 minutes. He used just two hourglasses. One measured 7 minutes and the other 11 minutes. During the whole time he turned the hourglasses only 3 times. How did he measure the 15 minutes?

TIEBREAKER #2 : SOLUTION When the test began, the professor started both the 11 min. and 7 min. hourglasses running. When the 7 min hourglass ran out, he flipped it over, while the 11 min hourglass continues. 4 minutes later, the 11 min hourglass ran out, and he promptly flipped the 7 min hourglass over again, so the 4 min ran back again. 11+4=15 , and the test was over.

TIEBREAKER #3 Assuming A, B, C, D, & E each represent different digits between 0 and 9, find the digits such that : ABCDE × 4 EDCBA Hint : Remember to carry your tens digits. Hint 2: Determine the digits in the following order A, E, B, D, C

TIEBREAKER #3 : SOLUTION • Since EDCBA must be a five digit number, A must be either 1 or 2; but it can’t be 1, since all multiples of 4 are even. • So E must be 3 or 8 (which make 12 or 32). But E can’t be 3, since no five digit number times 4 is less than 40, 000 (product can’t begin with 3). • Since EDCBA begins with 8, B × 4 must be either 1 or 0. But (Dx 4)+3 must be odd, so B must be 1. 3 ABCDE × 4 EDCBA 2 BCDE × 4 EDCB 2 2 BCD 8 × 4 8 DCB 2 3 21 CD 8 × 4 8 DC 12

TIEBREAKER #3 : SOLUTION • (Dx 4)+3 can only end in 1, if D is 2 or 7. But 2 has already been used as A. So D must be 7. • The only way to get 4 x 1 to be 7, is if there is a carried 3. Only 4 x 8 or 4 x 9 begin with 3. Since 8 has already been used as E, C must be 9. 3 21 CD 8 × 4 8 DC 12 3 21 C 78 × 4 87 C 12 3 3 2 1, 9 7 8 × 4 8 7, 9 1 2