WELCOME TO SYSTEM OF PARTICLES AND ROTATIONAL MOTION










































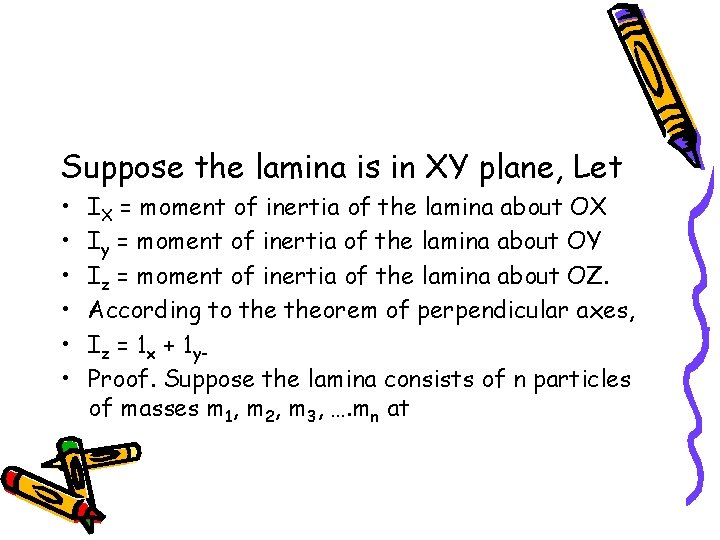

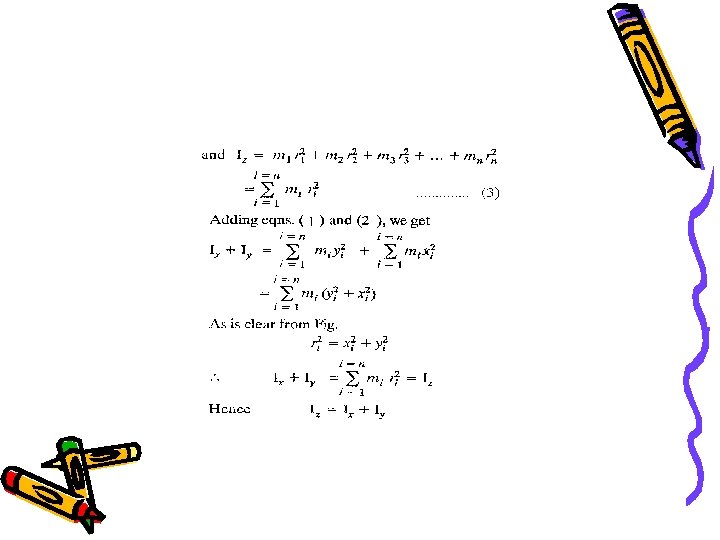



- Slides: 52

WELCOME TO SYSTEM OF PARTICLES AND ROTATIONAL MOTION

CENTRE OF MASS AND ROTATIONAL MECHANICS Pure Translation Motion In such a motion, every particle of the body has the same velocity at a particular instant of time. In such a motion, a rigid body rotates about a fixed axis. Every particle of the body moves in a circle, which lies in a plane perpendicular to the axis, and has its centre on the axis.

Combination of translational and rotational motion. The motion of a rigid body, which is not pivoted or fixed in some way is either a pure translation or a combination of translation and rotation. (ii) The motion of a rigid body, which is pivoted or fixed in some way is rotation. (i)

Concept Of Centre Of Mass l We may define centre of mass of a body or a system of bodies as a point at which the entire mass of the body system of bodies, is supposed to be concentrated.

Centre of Mass of a Two Particle System

Centre of Mass of a Two Particle System OA = r 1 ¡ OB = r 2 ¡ (m 1 + m 2) r = m 1 r 1 + m 2 r 2 ¡ For Center of Mass ¡ X = m 1 x 1 + m 2 x 2 m 1 + m 2 ¡ Y = m 1 v 1 + m 2 v 2 m 1 + m 2 ¡

Acceleration and Velocity of center of mass Vcm = m 1 v 1 + m 2 v 2 m 1 + m 2 Acm = m 1 a 1 + m 2 a 2 m 1 + m 2 - - - + m nv n - + m 2 - - m nan - mn

Derivation o o o f 1 = external force applied on particle of mass m 1 F 2 = external force applied on particle of mass m 2 F 12 = internal force on m 1 due to m 2 F 21=internal force on m 2 due to m 1 Linear momentum of particle m 1 is P 1 = m 1 v 1

F 12 = -f 21 F 12 + f 21=0 Acc. To Newton’s Second law I = dp dt For m 1: F 10= dp 1 = d(m 1 v 1) - - (1) dp dt

for M 2 : F 12 + F 21 = dp 2 dt = d(m 2 v 2) dt (1) + (2) : F 1 + F 2 = d (m 1 v 1+m 2 v 2) dt -- -- (2)

F (total) = d [ m 1 dv 1 + m 2 dv 2 dt dt 1 dt 2 F(total) = d (d (m 1 r 1 + m 2 r 2) dt dt f (total) = d 2 (m 1 r 1 + m 2 r 2) dt 2 F(total) = m 1 + m 2 d 2 (m 1 r 1 + m 2 r 2) dt 2

o F(total) = m 1 + m 2 dt 2 F = ma = mdr dt t = md dr dt dt F = md 2 r dt 2 = r = m 1 r 1 + m 2 r 2 m 1 + m 2

Momentum Conservation and motion at the centre of mass o F(total) = d (mivi) dt f(t) = d (m 1 v 1 + m 2 v 2 - - mnvn) dt Total force = 0 d (m 1 v 1 + m 2 v 2 - - - mnvn) = 0 dt d (const. ) = 0 dt m 1 v 1 + m 2 v 2 + m 3 v 3 - - mnvn = const.

For centre of mass also o F = ma o F=m F=0 mdv = 0 dt m≠ 0 so, dv = 0 dt dv dt (only when v = constant)

Examples Of The Motion Of Centre Of Mass • A special type of cracker which when ignited goes up in the sky and then explodes into many firry pieces. The centre of mass of the fragment will move on its initial parabolic path.

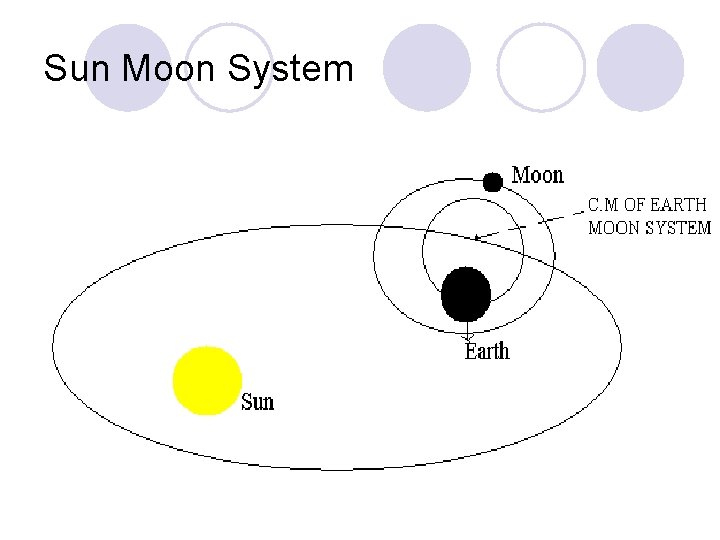
Sun Moon System l Moon revolves around the earth in a circular orbit and the earth moon system goes round the sun in elliptical orbit (as shown), Both Earth & moon move along the circular paths about their cm such that they are always on opp. Sides of it. It is the cm of earth l moon system that exactly follow the elliptical path around the sun.

Sun Moon System

Radioactive Nucleus n When a radioactive nucleus initially at rest, decays into two fragments which fly apart obeying the laws of conservation of momentum , centre of mass of the two fragments. Remain at rest.

Angular Velocity For rotation about a fixed axis, the angular velocity vector lies along the axis of rotation and points out in which the tip of right handed screw would advanced if the head of the screw is rotated with the body. ω = dθ dt

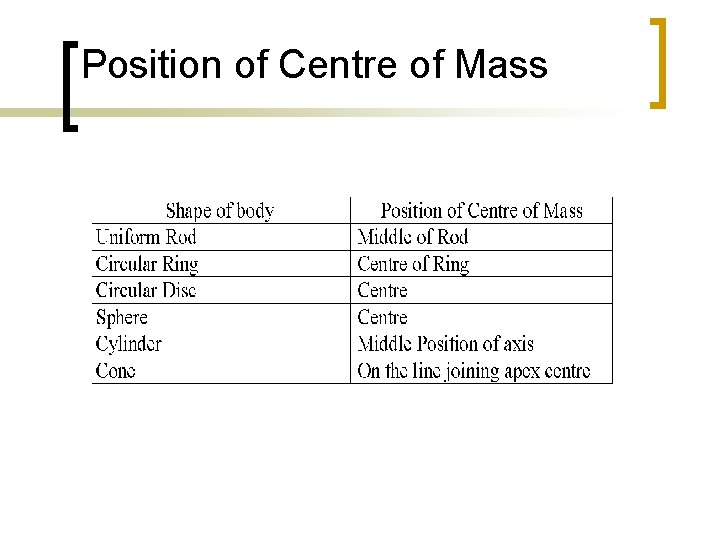
Position of Centre of Mass

#Analog between Linear & Rotational Motion:

Analog between Linear & Rotational Motion:

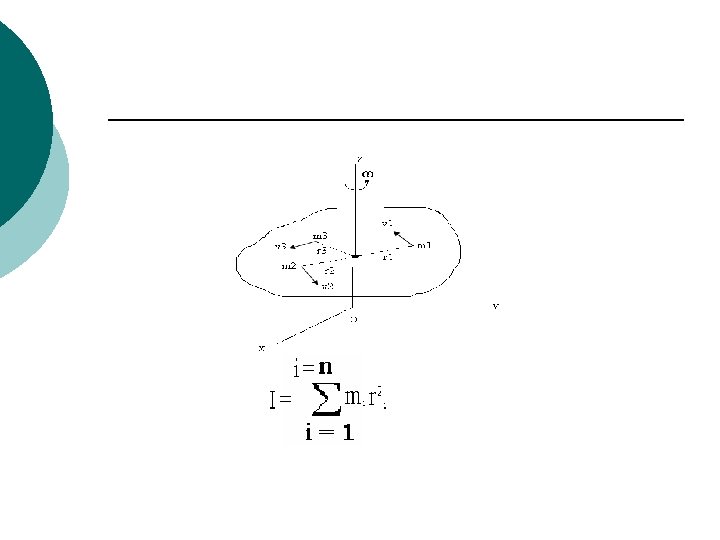
Rigid body Is regarded as a assembly of unit masses. The mutual distances among the different point masses do not change during the motion of rigid body.

Angular Acceleration l l l Angular acceleration of an object in circular motion is defined us the time rate of its angular velocity. It is represented by Greek letter α (alpha). i. e. , angular acceleration = change in angular velocity Time taken

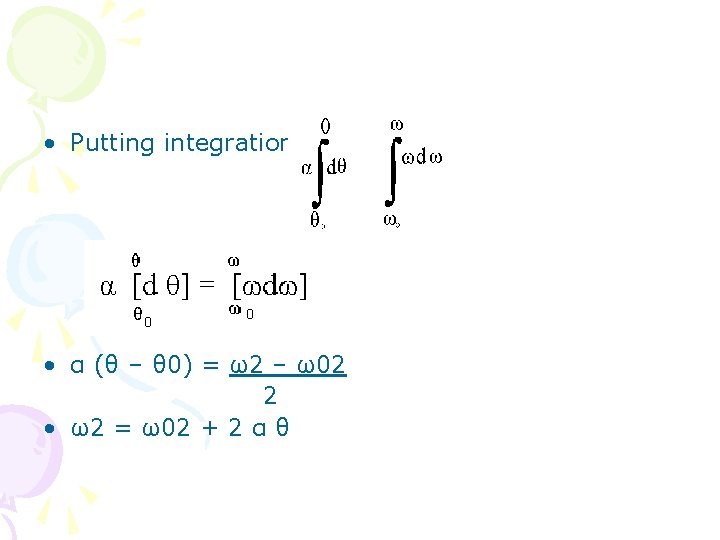
Derivation Of Equations ω = ω0 + αt • α = dω dt • Putting integration : • αα (t-0) = ω (ω-ω0) • α t =-ωo+ αt _ _ • dt = dω] • ω = ω0 + αt (1)




Law of Conservation of Angular Momentum • T = d. L dt • T=0 • d. L = 0 dt • since L = const. • L=rxp • = r x m 1 v • = r x m x rω • L = mr 2ω • L=I ω So, I ω = const.

KINETIC ENERGY OF ROLLING MOTION l. K = KT = KR l If m is the mass of the body & v cm is velocity l of centre of mass of the body, then l KE of translation, KT = 1/2 mv 2 l KE of rotation, kr = ½ Iω2 l Where I = moment of inertia

l l l KE of rolling body, K = ½ mv 2 cm+ 1/2 Iω2 Vcm = Rω ω = Vcm R K = 1/2 mv 2 cm + ½ mk 2 Vcm R K = ½ mv 2 cm = [1+ k 2] R 2

Laws of Rotational Motion n Corresponding to Newton’s three laws of translational motion, we can state three laws of rotational motion as follows: n A body continues to be in a state of rest or in a state of uniform rotation about a given axis unless an external torque is applied on the body. n The rate of change of angular momentum of a body about a given axis is directly proportional to the external torque applied on the body. n When a rigid body A exerts a torque on another rigid body B in contact with it, then the body B would exert an equal and opposite torque on the body A.

Moment of Inertia n This force varies directly as the mass of the body. Hence mass of a body is a measure of inertia of the body in linear motion. n A quantity that measures the inertia of rotational motion of the body is called rotational inertial or moment of inertia of the body. n Kinetic Energy of Rotation

n Kinetic energy of rotation of a body is the energy possessed by the body on account of its rotation about a given axis. n This force varies directly as the mass of the body. Hence mass of a body is a measure of inertia of the body in linear motion.

n This force varies directly as the mass of the body. Hence mass of a body is a measure of inertia of the body in linear motion. n A quantity that measures the inertia of rotational motion of the body is called rotational inertial or moment of inertia of the body. n Kinetic Energy of Rotation n Kinetic energy of rotation of a body is the energy possessed by the body on account of its rotation about a given axis.

A quantity that measures the inertia of rotational motion of the body is called rotational inertial or moment of inertia of the body. Kinetic Energy of Rotation Kinetic energy of rotation of a body is the energy possessed by the body on account of its rotation about a given axis.


Radius of Gyration o The radius of gyration of a body about a given axis is the perpendicular distance of a point P from the axis, where if whole mass of the body were concentrated, the body shall have the same moment of inertia as it has with the actual distribution of mass.

o K = r 12 + r 22 + …r n 2 n o Radius of gyration of a body about a given axis is equal to root mean square distance of the constituent particles of the body from the given axis.

Relation between Torque and Angular Momentum of a Rigid Body. o L=In o Differentiating body sides w. r. t. t, we get o d. L = I dw = Iα dt dt o where α = dw = angular acceleration of the body. dt o But torque, T= Iα o From above equation o T = dl dt

Principle of Conservation of Angular Momentum o When no external torque acts on a system of particles, then the total angular momentum of the system remains always a constant. o When no external torque acts on the system, o d dt o or

THEOREM OF PARALLEL AXES: o According to this theorem, momentum of inertia of a rigid body about any axis AB is equal to moment of inertia of the body about another axis KL passing through centre of mass C of the body in a direction parallel to AB, plus the product of total mass M of the body and square of the perpendicular distance between the two parallel axes. o IAB = IKL + Mh 2

THEOREM OF PARALLEL AXES: Proof. Suppose the rigid body is made up of n particles of masses m 1, m 2, m 3 …. . mn at perpendicular distances r 1, r 2, r 3 …. rn respectively from the axis KL passing through centre of mass C of the body. If ri is the perpendicular distance of a particle of mass mi from KL, then

• The perpendicular distance of ith particle from the axis KL = (ri + h)


Theorem of Perpendicular Area • According to this theorem, the moment of inertia of a plane lamina (i. e. a two dimensional body of any shape/size) about any axis OZ perpendicular to the plane of the lamina is equal to sum of the moments of inertia of the lamina about any two mutually perpendicular axes OX and OY in the plane of the lamina, meeting at a point where the given axis OZ passes through the lamina.
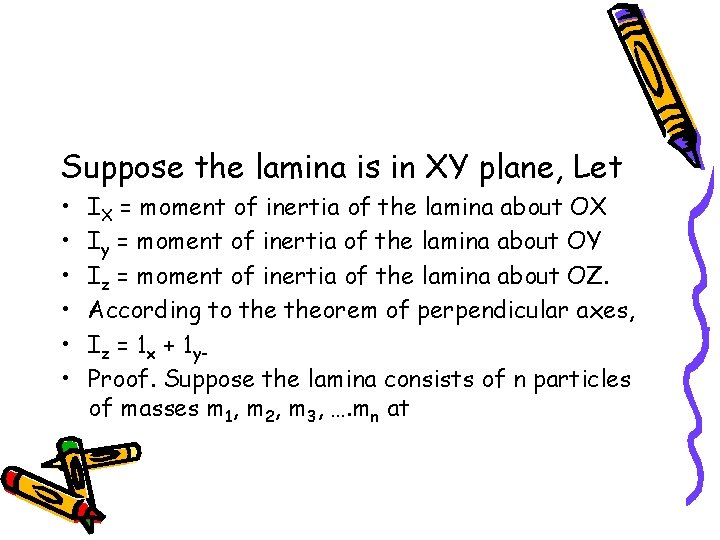
Suppose the lamina is in XY plane, Let • • • IX = moment of inertia of the lamina about OX Iy = moment of inertia of the lamina about OY Iz = moment of inertia of the lamina about OZ. According to theorem of perpendicular axes, Iz = 1 x + 1 y Proof. Suppose the lamina consists of n particles of masses m 1, m 2, m 3, …. mn at

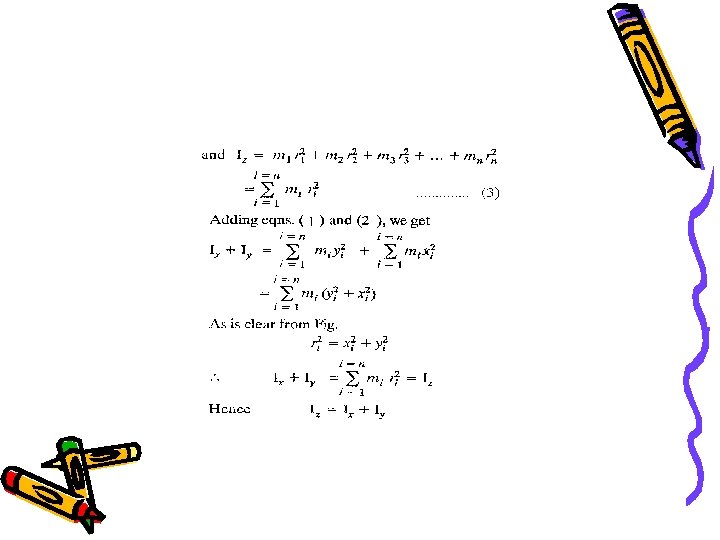

KINETIC ENERGY OF ROLLING MOTION n n n K = KT = KR If m is the mass of the body & v cm is velocity of centre of mass of the body, then KE of translation, KT = 1/2 mv 2 KE of rotation, kr = ½ Iω2 Where I = moment of inertia KE of rolling body, K = ½ mv 2 cm+ 1/2 Iω2 Vcm = Rω ω = Vcm R K = 1/2 mv 2 cm + ½ mk 2 Vcm R K = ½ mv 2 cm = [1+ k 2] R 2

Laws of Rotational Motion n Corresponding to Newton’s three laws of translational motion, we can state three laws of rotational motion as follows: n A body continues to be in a state of rest or in a state of uniform rotation about a given axis unless an external torque is applied on the body. n The rate of change of angular momentum of a body about a given axis is directly proportional to the external torque applied on the body. n When a rigid body A exerts a torque on another rigid body B in contact with it, then the body B would exert an equal and opposite torque on the body A.

THANK YOU For going through the