Welcome to CS 235 Data Structures Recursion 7

Welcome to CS 235 Data Structures Recursion, 7. 3 -4 (23)

7. 1 Recursive Thinking Steps to Design a Recursive Algorithm Proving That a Recursive Function Is Correct Tracing a Recursive Function The Stack and Activation Frames 2 7. 1, pgs. 404 -411

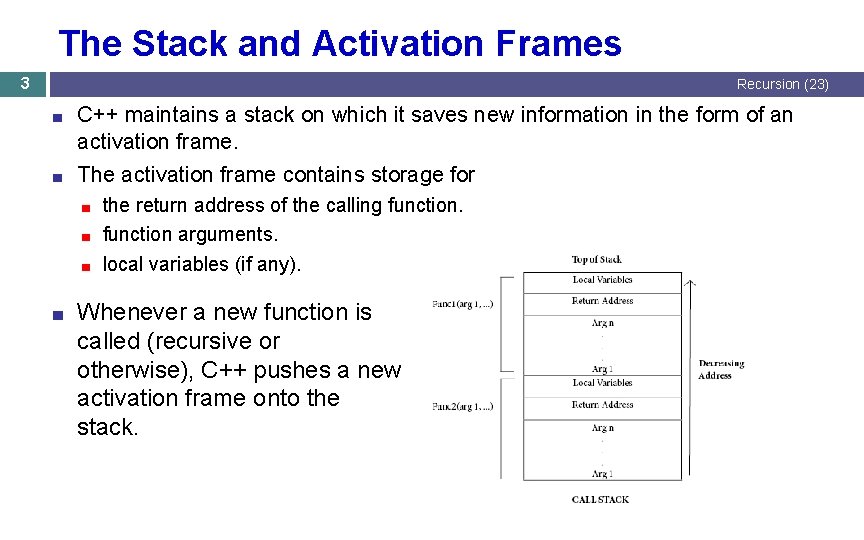
The Stack and Activation Frames 3 Recursion (23) ■ C++ maintains a stack on which it saves new information in the form of an activation frame. ■ The activation frame contains storage for the return address of the calling function. ■ function arguments. ■ local variables (if any). ■ ■ Whenever a new function is called (recursive or otherwise), C++ pushes a new activation frame onto the stack.

Tracing a Recursive Function 4 Recursion (23) ■ The process of returning from recursive calls and computing the partial results is called unwinding the recursion. #include <iostream> using namespace std; int size(string str) { if (str == "") return 0; return 1 + size(str. substr(1)); } int main() { cout << size("ace"); return 0; } cout << size("ace"); 3 return 1 + size("ce") 2 return 1 + size("e") 1 return 1 + size("") 0

Run-Time Stack - Activation Frames 5 Recursion (23) int main() { cout << size("ace"); return 0; } int size(string str) { if (str == "") return 0; return size(str. substr(1)); }

7. 2 Recursive Definitions of Mathematical Formulas Recursion Versus Iteration Tail Recursion or Last-Line Recursion Efficiency of Recursion 6 7. 2, pgs. 412 -419

Recursive Mathematical Formulas 7 Recursion (23) ■ Mathematicians often use recursive definitions of formulas that lead naturally to recursive algorithms ■ Examples include: factorials ■ powers ■ greatest common divisors ■ sorts ■ int factorial(int n) { if (n <= 1) return 1; return (n * factorial(n – 1)); } x = factorial(4) 24 return 4 * factorial(3) 6 return 3 * factorial(2) 2 return 2 * factorial(1) 1

Calculating xn 8 Recursion (23) ■ You can raise a number to a power that is greater than 0 by repeatedly multiplying the number by itself. ■ Recursive definition: xn = x xn-1 ■ Base case: x 0 = 1 /** Recursive power function @param x: The number @param n: The exponent @return x raised to the power n */ double power(double x, int n) { if (n == 0) return 1. 0; if (n > 0) return x * power(x, n – 1); else return 1. 0 / power(x, -n); } x = power(2. 0, -3) 0. 125 return 1. 0 / power(2. 0, 3) 8. 0 return 2. 0 * power(2. 0, 2) 4. 0 return 2. 0 * power(2. 0, 1) 2. 0 return 2. 0 * power(2. 0, 0) 1. 0

Trace the call stack of the following recursive Greatest-Common. Divisor function for gcd(30, 77). /** Recursive Greatest Common Divisor function @param m The larger number (m > 0) @param n The smaller number (n > 0) @return gcd of m and n */ int gcd(int m, int n) { if (m % n == 0) return n; if (m < n) return gcd(n, m); return gcd(n, m % n); } x = gcd(30, 77) return m n gcd( , ) gcd( , )

Calculating GCD Correct? 10 Recursion (23) ■ How do we verify that our algorithm is correct? ■ Base correct? The base case is “n is a divisor of m” ■ The solution is n (n is the greatest common divisor), which is correct ■ ■ Does recursion make progress to base case? Both arguments in each recursive call are smaller than in the previous call and ■ The new second argument is always smaller than the new first argument (m % n must be less than n) ■ Eventually a divisor will be found or the second argument will become 1 (which is a base case because it divides every integer) ■

Recursion Downside 11 Recursion (23) ■ Recursion downside ■ Base case never reached. Factorial with a negative argument - throw an invalid_argument exception if n is negative. ■ You will eventually get a run-time error when there is no more memory available for your program to execute more function calls. ■ ■ ■ Error deep in recursion stack. Recursion vs Iteration ■ There are similarities between recursion and iteration. In iteration, a loop repetition condition determines whether to repeat the loop body or exit from the loop. ■ In recursion, the condition usually tests for a base case. ■ ■ There is always an iterative solution to a problem that is solvable by recursion. ■ A recursive algorithm may be simpler than an iterative algorithm and thus easier to design, code, debug, and maintain.

Tail Recursion 13 Recursion (23) ■ Most of the recursive algorithms and functions so far are examples of tail recursion or last-line recursion. ■ ■ In these algorithms, there is a single recursive call and it is the last line of the function, such as in the factorial function. Straightforward process to turn a recursion function with a tail into an iterative solution: /** Recursive factorial function */ int factorial(int n) { if (n <= 1) return 1; return n * factorial(n – 1); } /** Iterative factorial function */ int factorial_iter(int n) { int result = 1; for (int k = 1; k <= n; k++) result = result * k; return result; }

Fibonacci Numbers 15 Recursion (23) f(n) = f(n-1) + f(n-2) f(0) = 1 f(1) = 1 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987… int Fibonacci(int n) { if (n < 2) return 1; /* base case */ return (Fibonacci(n-1) + Fibonacci(n-2)); }

Call Tree for Fibonacci 16 Recursion (23) main() Fibonacci(4) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 17 Recursion (23) main() Fibonacci(4) Fibonacci(3) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 18 Recursion (23) main() Fibonacci(4) Fibonacci(3) Fibonacci(2) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 19 Recursion (23) main() Fibonacci(4) Fibonacci(3) Fibonacci(2) Fibonacci(1) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 20 Recursion (23) main() Fibonacci(4) Fibonacci(3) Fibonacci(2) 1 Fibonacci(1) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 21 Recursion (23) main() Fibonacci(4) Fibonacci(3) Fibonacci(2) 1 Fibonacci(1) Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 22 Recursion (23) main() Fibonacci(4) Fibonacci(3) Fibonacci(2) 1 1 Fibonacci(1) Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 23 Recursion (23) main() Fibonacci(4) Fibonacci(3) Fibonacci(2) + 1 1 Fibonacci(1) Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 24 Recursion (23) main() Fibonacci(4) Fibonacci(3) 2 Fibonacci(2) + 1 1 Fibonacci(1) Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 25 Recursion (23) main() Fibonacci(4) Fibonacci(3) 2 Fibonacci(2) + 1 1 Fibonacci(1) Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 26 Recursion (23) main() Fibonacci(4) Fibonacci(3) 2 Fibonacci(2) 1 + 1 1 Fibonacci(1) Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 27 Recursion (23) main() Fibonacci(4) Fibonacci(3) 2 Fibonacci(2) + 1 1 Fibonacci(1) Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 28 Recursion (23) main() Fibonacci(4) 3 Fibonacci(3) 2 Fibonacci(2) + 1 1 Fibonacci(1) Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 29 Recursion (23) main() Fibonacci(4) 3 Fibonacci(3) 2 Fibonacci(2) + 1 1 Fibonacci(1) Fibonacci(2) Fibonacci(1) Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 30 Recursion (23) main() Fibonacci(4) 3 Fibonacci(3) 2 Fibonacci(2) + 1 1 Fibonacci(1) Fibonacci(2) Fibonacci(1) Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 31 Recursion (23) main() Fibonacci(4) 3 Fibonacci(3) 2 Fibonacci(2) + 1 1 Fibonacci(1) Fibonacci(2) 1 Fibonacci(1) Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 32 Recursion (23) main() Fibonacci(4) 3 Fibonacci(3) 2 Fibonacci(2) + 1 1 Fibonacci(1) Fibonacci(2) 1 Fibonacci(1) Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 33 Recursion (23) main() Fibonacci(4) 3 Fibonacci(3) 2 Fibonacci(2) + 1 1 Fibonacci(1) Fibonacci(2) 1 Fibonacci(1) 1 Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 34 Recursion (23) main() Fibonacci(4) 3 Fibonacci(3) 2 Fibonacci(2) + 1 1 Fibonacci(1) Fibonacci(2) 1 Fibonacci(1) + 1 Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Call Tree for Fibonacci 35 Recursion (23) main() Fibonacci(4) 3 Fibonacci(3) 2 Fibonacci(2) + 1 1 Fibonacci(1) 2 Fibonacci(2) 1 Fibonacci(1) + 1 Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

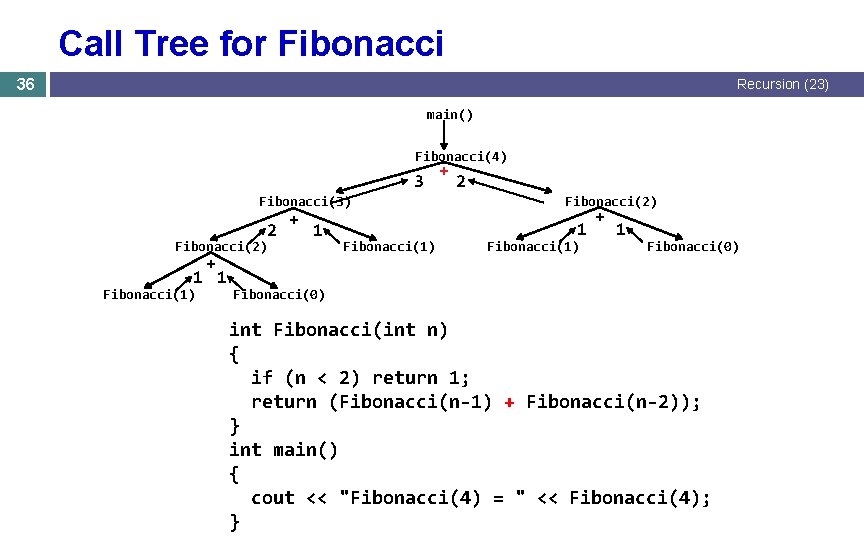
Call Tree for Fibonacci 36 Recursion (23) main() Fibonacci(4) 3 Fibonacci(3) 2 Fibonacci(2) + 1 1 Fibonacci(1) + 2 Fibonacci(2) 1 Fibonacci(1) + 1 Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

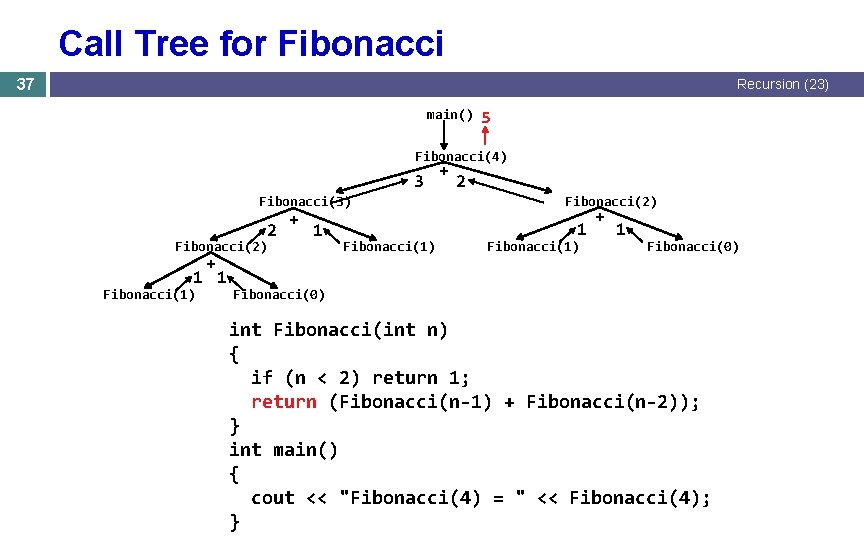
Call Tree for Fibonacci 37 Recursion (23) main() 5 Fibonacci(4) 3 Fibonacci(3) 2 Fibonacci(2) + 1 1 Fibonacci(1) + 2 Fibonacci(2) 1 Fibonacci(1) + 1 Fibonacci(0) int Fibonacci(int n) { if (n < 2) return 1; return (Fibonacci(n-1) + Fibonacci(n-2)); } int main() { cout << "Fibonacci(4) = " << Fibonacci(4); }

Fibonacci Numbers O(n) 38 Recursion (23) ■ Because of the redundant function calls, the time required to calculate fibonacci(n) increases exponentially with n. If n is 100, there approximately 2100 activation frames ( 1030). ■ If you could process one million activation frames per second, it would still take 1024 seconds ( 3 � 1016 years) to compute fibonacci(100). ■ /** Recursive O(n) function to calculate Fibonacci numbers @param fib_current The current Fibonacci number @param fib_previous The previous Fibonacci number @param n The count of Fibonacci numbers left to calculate @return The value of the Fibonacci number calculated so far */ int fibo(int fib_current, int fib_previous, int n) { if (n == 1) return fib_current; return fibo(fib_current + fib_previous, fib_current, n – 1); }

Fibonacci Numbers O(n) 39 Recursion (23) /** Fibonacci sequence fibonacci(4) @param fib_current Current # 5 @param fib_previous Previous # @param n # left to calculate fibo(1, 1, 4) @return Current Fibonacci value 5 */ int fibo(int current, int previous, int n) fibo(2, 1, 3) { 5 if (n < 2) return current; return fibo(current + previous, current, n - 1); fibo(3, 2, 2) } 5 int fibonacci(int n) { fibo(5, 3, 1) return fibo(1, 1, n); } int main() { cout << "Fibonacci(4) = " << fibonacci(4); }

7. 3 Recursive Search Design of a Recursive Linear Search Algorithm Implementation of Linear Search Design of Binary Search Algorithm Efficiency of Binary Search Implementation of Binary Search Testing Binary Search 40 7. 3, pgs. 420 -426

Recursive vector Search 41 Recursion (23) ■ Searching a vector can be accomplished using recursion. ■ The simplest way to search is a linear search: Examine one element at a time starting with the first element or the last element to see whether it matches the target. ■ On average, approximately n/2 elements are examined to find the target in a linear search. ■ If the target is not in the vector, all n elements are examined. ■ ■ Base cases for recursive search: Empty vector, target can not be found; result is -1. ■ First element of the vector matches the target; result is the subscript of first element. ■ ■ The recursive step searches the rest of the vector, excluding the first element. ■ What is the order of complexity? O(n).

Recursive vector Search 42 Recursion (23) /** Recursive linear search function @param items The vector being searched @param target The item being searched for @param first The position of the current first element @return The subscript of target if found; otherwise -1 */ template<typename T> int linear_search(const vector<T>& items, const T& target, size_t first) { if (first == items. size()) return -1; if (target == items[first]) return first; return linear_search(items, target, first + 1); } /** Wrapper for recursive linear search function */ template<typename T> int linear_search(const std: : vector<T>& items, const T& target) { return linear_search(items, target, 0); }

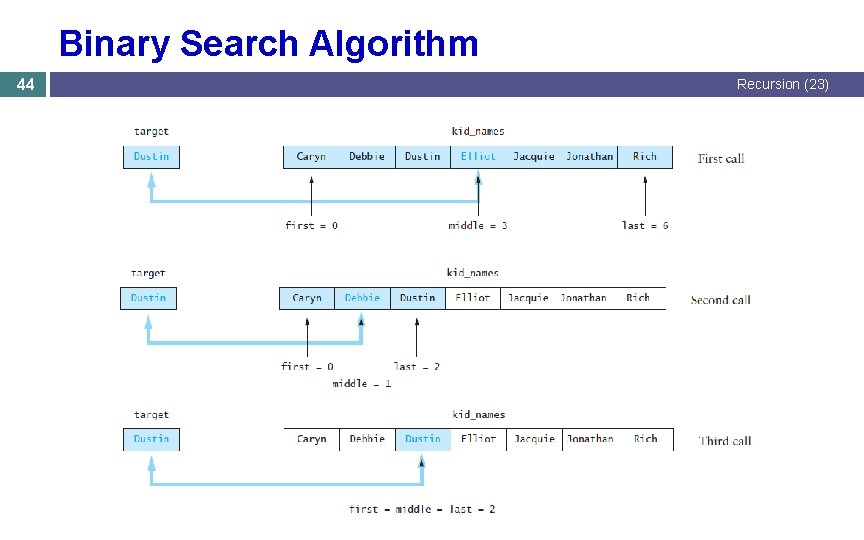
Design of a Binary Search Algorithm 43 Recursion (23) ■ A binary search can be performed only on an array or vector that has been sorted. ■ Base cases: The range of the vector is empty. ■ The element being examined matches the target. ■ ■ Rather than looking at the first element, a binary search compares the middle element for a match with the target. ■ If the middle element does not match the target, a binary search excludes the half of the vector (within which the target would not be found. ) ■ What is the order of complexity? O(log n).

Binary Search Algorithm 44 Recursion (23)

Efficiency of Binary Search 45 Recursion (23) ■ At each recursive call we eliminate half the vector elements from consideration, making a binary search O(log n). ■ A vector of size 16 would search vectors of length 16, 8, 4, 2, and 1, making 5 probes in the worst case. 16 = 24 ■ 5 = log 2 16 + 1 ■ ■ A doubled vector size would require only 6 probes in the worst case. 32 = 25 ■ 6 = log 2 32 + 1 ■ ■ A vector with 32, 768 elements requires only 16 probes! ■ A vector of 65, 536 elements increases the number of required probes to 17.

Recursive Binary Search 46 Recursion (23) template <typename T> int binary_search(const vector<T>& items, int first, int last, const T& target) { if (first > last) return -1; // (base case #1) size_t middle = (first + last) / 2; // next probe if (target == items[middle]) return middle; //success (base case #2) if (target < items[middle]) return binary_search(items, first, middle - 1, target); else return binary_search(items, middle + 1, last, target); } /** Wrapper for recursive binary search function */ template<typename T> int binary_search(const vector<T>& items, const T& target) { return binary_search(items, 0, items. size() - 1, target); }