WELCOME Algebra Chapter 1 SETS My bouquet a

WEL-COME Algebra Chapter: -1 SETS

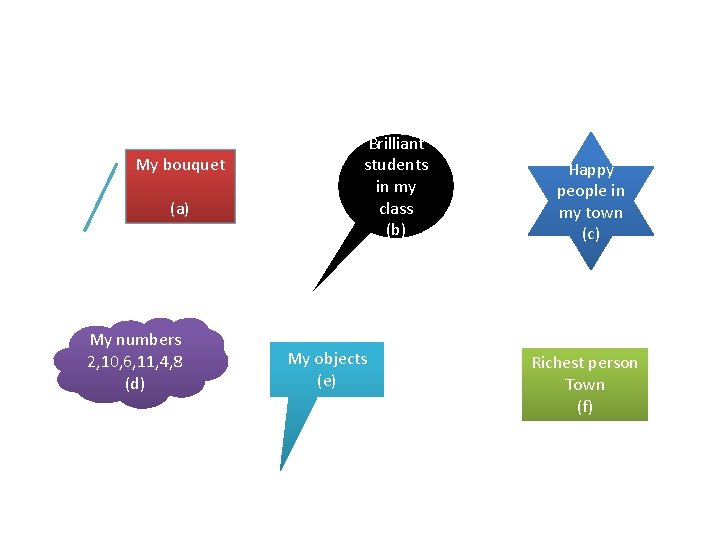
My bouquet (a) My numbers 2, 10, 6, 11, 4, 8 (d) Brilliant students in my class (b) My objects (e) Happy people in my town (c) Richest person Town (f)

• The objects in the posters of (a), (d), (e)are clearly seen. • Such collections are well defined collections. • • The names of students or persons in posters (b), (c), (f) are not one and the same , such collections are not well defined collections. • A well defined collection of objects is called a set. • Individual object in the set is called an element or member of the set. • Sets are denoted by capital alphabets e. g. A, B, C, etc. The elements of sets are generally denoted by small alphabets e. g. a, b, c etc. • If x is an element of the set X then we write it as xє X and if x is not an element of set X then we write x є X. • (є: belongs to , є: does not belongs to)

Common notations (a) N= the set of nonnegative integers or natural number={1, 2, 3, . . . } (b) W= the set of whole numbers= {0, 1, 2, 3, . . . } (c) I=the set of integers={…, -3, -2, -1, 0, 1, 2, 3, . . . } (d) Q=the set of rational number. (e) R=the set of real numbers

Sets Methods of writing sets • (a) Listing method(Roster form) • (b)Rule method(Set builder orm) Chapt. -Sets

Sets • LISTING METHOD(Roster form) • In this method , first write the name of the set , put is equal sign and write all its elements enclosed within curly brackets{ }. • Elements are separated by commas. • An element , even if repeated , is listed only once. • The order of the elements in a set is immaterial.

• e. g. 1) The set of all natural numbers less than ten. • A={1, 2, 3, 4, 5, 6, 7, 8, 9} • 2) The set of colours in the rainbow. • B={red , orange , yellow , green, blue, indigo, voilet} • 3) C =The set of letters in the word ‘MATHEMATICS’ • C={m , a , t , h , i , c , s}

Rule Method(Set builder form) In the set builder form we describe the elements of the set by specifying the property or rule that uniquely determines the elements of the set. Consider the set P={1, 4, 9, 16, } P={x x =n 2, nєN , n=1, 2, 3, 4, 5} In this notation , the curly bracket stands for ‘the set of ’, vertical line stands for, such that. Here ‘x’ represents each elements of that set. And read as “P is the set of all x such that x is equal to n 2, where n є N and n is less than or equal to 5. ”

• e. g. 1)The set of prime numbers from 1 to 20 • A={2, 3, 5, 7, 11, 13, 17, 19} • This can be written in set builder form as : • A={x x is a prime number less than 20 } • 2)B={-7, 7} • B={x: xis a square root of 49}

Shri Londhe P R L. B. P Vidyalaya , Ahmednagar