Weights The Heart of Least Squares From Chapter

Weights: The Heart of Least Squares From Chapter 8 of Errors in Practical Measurement in Surveying, Engineering and Technology by B. Austin Barry Land Surveyors’ Association of Washington 2014 Annual Conference Presentation March 6, 2014 by Jon B. Purnell, PLS © 2014 Alidade Consulting

Weights: • identify measurements that are more reliable • quantifies the degree of reliability of various measurements • allows a measurement to exert its proper influence in a mean or adjustment

Weights: • assigned via judgement of observer • set by use of indexes • assigned in proportion to the number of observations made • derived from modeling: computation of Standard Deviation or Standard Error of the Mean

Weighted Mean Example: • • Given, measurements and weights: 244. 43’ measured 5 times 244. 25’ measured 50 times A simple arithmetic mean ignores weights:

Weighted Mean: • A weighted mean gives more weight (influence) to more reliable measurements: • Given: A = 244. 43’ (mean of 5 measurements) B = 244. 25’ (mean of 50 measurements) • We want to place more reliance (weight) on B because it is derived from 10 times more measurements • The measurements’ weights differ by a factor of 10, so B is has 10 times more weight than A

Computing Weighted Mean: • A (244. 43) has a weight of = 5 • B (244. 25) has a weight of = 50 • Weighted mean of A and B =

Weighted Mean Bearings Prevents short lines from exerting undue influence on computed section centerline Weights come from line lengths

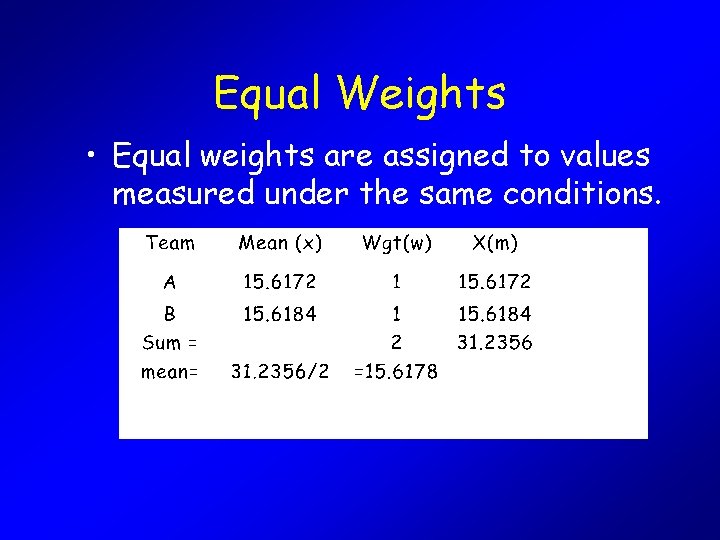
Rules for Assigning Weights • Equal weights are assigned to values measured under the same conditions. • The more times a quantity is measured the more weight it should receive • Weights derived from standard errors are set proportional to the inverse square of the Standard Error (smaller SE = more weight)

Equal Weights • Equal weights are assigned to values measured under the same conditions.

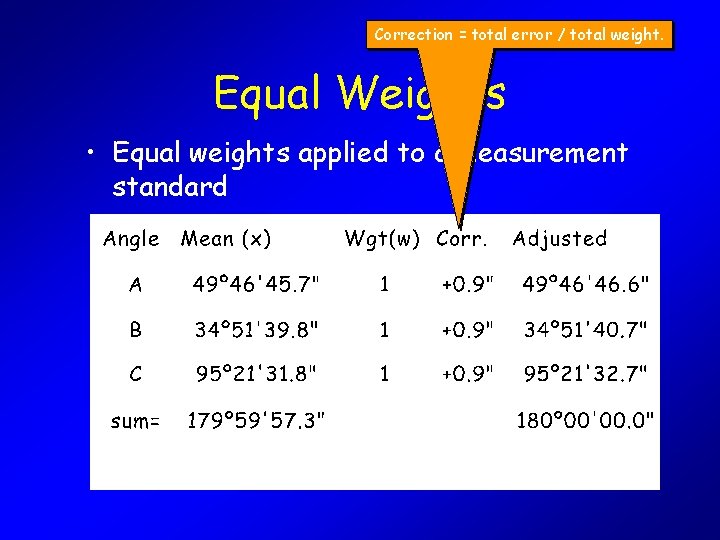
Correction = total error / total weight. Equal Weights • Equal weights applied to a measurement standard

Weights and Standard Error • As n increases, Standard Error decreases • Standard Error varies inversely with the square root of n

Weights and Standard Error • Since weights are assigned in proportion to the number of observations… • weights vary inversely with the square the standard errors

Weights and Standard Error Which value has the most weight? Which value has the least weight?

Measurement with Inverse Other largest Square weights Standard Measurement of = (1/SE)^2/(1/155)^2 the Error Standard assigned multiplied Error Weight by Weight = 1. 0000 Weights and Standard Error Weighted Mean = 299077. 2/7. 5173 =39785 psi

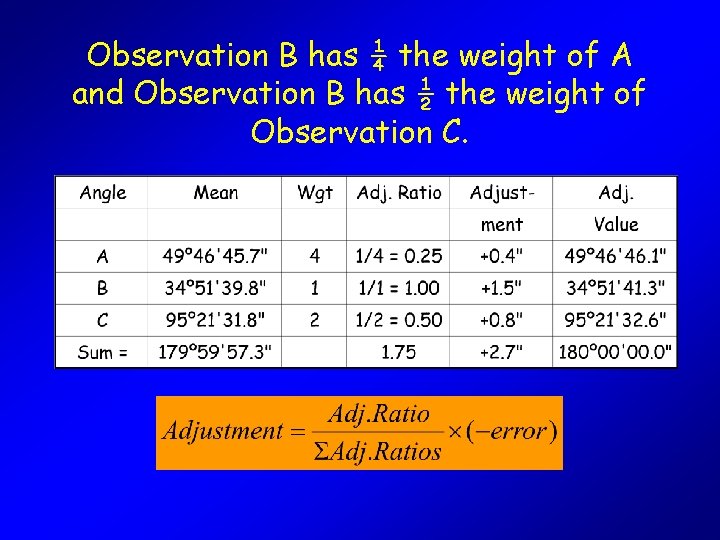
Weights and Adjustments • A measurement having a high weight should not be adjusted as much as a measurement having a low weight (think: heavier = harder to move) • Therefore, adjustments (or corrections) to measurements are inversely related to weight (more weight, less adjustment)

Observation B has ¼ the weight of A and Observation B has ½ the weight of Observation C.

Standard Errors, Weights and Adjustments • If each measurement is assigned a different Standard Error, each measurement will have a different weight

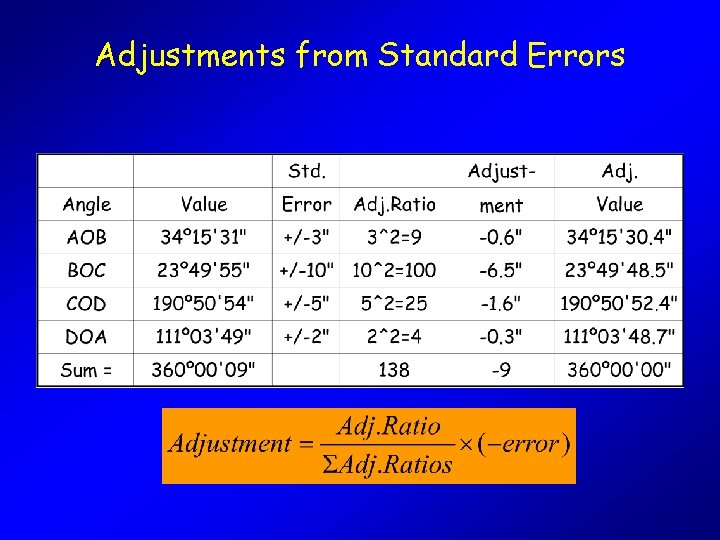
Standard Errors, Weights and Adjustments • Since weights are inversely related to Standard Errors, and adjustments are inversely related to weights, adjustments can be made in direct proportion to the Standard Errors • Measurements with smaller Standard Errors receive smaller adjustments (corrections)

Adjustments from Standard Errors Which value should receive the largest adjustment?

Adjustments from Standard Errors

Putting it in Star*Net Terms • Star*Net adjusts measurements in direct proportion to their Standard Errors… • …so measurements with smaller Standard Errors receive smaller adjustments • For the adjustment to be valid, you must have realistic Standard Errors!

Putting it in Star*Net Terms • You should develop your own Standard Errors for the various kinds of measurements you perform – Distances: Use the manufacturer’s EDM specification (i. e. +/-3 mm+3 ppm) – Angles: Set up a model situation, and develop SE for each operator and each instrument

Putting it in Star*Net Terms • You should develop your own Standard Errors for the various kinds of measurements you perform – Centering Errors: Keep tribrachs adjusted. Typical centering error is +/2 mm – Mixing data: Chained distances can be accurate to 1: 10000 IF precision procedures were used. USE YOUR JUDGEMENT.

Putting it in Star*Net Terms • Adjustments are called “residuals” in Star*Net – Difference between measured and adjusted values…. –. . . = adjustment = correction = residual

Putting it in Star*Net Terms • Star*Net compares a measurement’s residual with its Standard Error to see the how much a measurement got “tweaked” • The ratio of the residual to the Standard Error is called the Standardized Residual

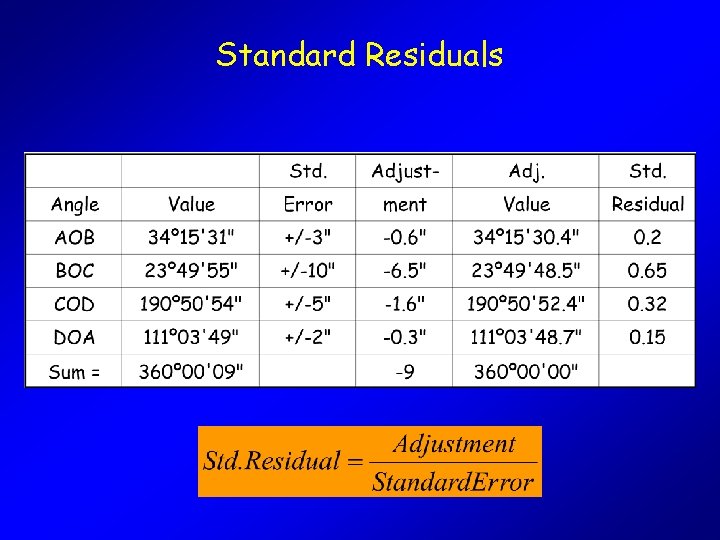
Putting it in Star*Net Terms • Standardized Residual – Residual = 0. 6”, Standard Error = 3” – Std. Residual =. 6/3, =. 2 – In other words, a residual of. 6 is 20% of this measurement’s Standard Error – This means that this measurement was “tweaked” less than the value predicted by our Standard Error!

Putting it in Star*Net Terms • Standardized Residual – Std. Residuals < 1 are GOOD THINGS – Std. Residuals > 1 are not so good. Too many of these in an adjustment will have adverse affects (check for systematic errors!) – Std. Residuals >2 may be indicative of blunders – Std. Residuals >3 most likely are blunders

Standard Residuals

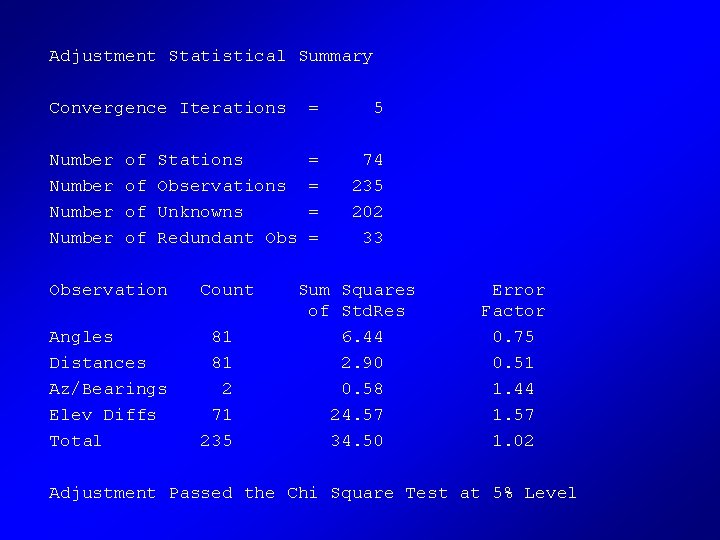
Adjustment Statistical Summary Convergence Iterations = 5 Number = = 74 235 202 33 of of Stations Observations Unknowns Redundant Observation Count Angles Distances Az/Bearings Elev Diffs Total 81 81 2 71 235 Sum Squares of Std. Res 6. 44 2. 90 0. 58 24. 57 34. 50 Error Factor 0. 75 0. 51 1. 44 1. 57 1. 02 Adjustment Passed the Chi Square Test at 5% Level

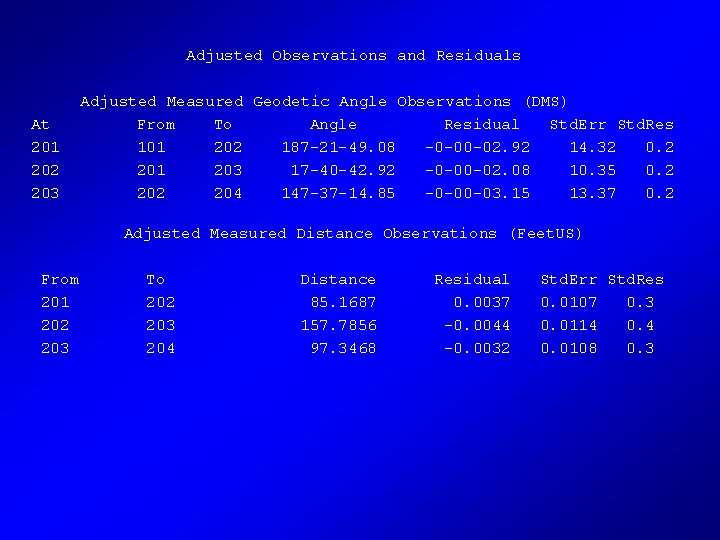
Adjusted Observations and Residuals At 201 202 203 Adjusted Measured Geodetic Angle Observations (DMS) From To Angle Residual Std. Err Std. Res 101 202 187 -21 -49. 08 -0 -00 -02. 92 14. 32 0. 2 201 203 17 -40 -42. 92 -0 -00 -02. 08 10. 35 0. 2 204 147 -37 -14. 85 -0 -00 -03. 15 13. 37 0. 2 Adjusted Measured Distance Observations (Feet. US) From 201 202 203 To 202 203 204 Distance 85. 1687 157. 7856 97. 3468 Residual 0. 0037 -0. 0044 -0. 0032 Std. Err Std. Res 0. 0107 0. 3 0. 0114 0. 0108 0. 3

All this leads to Positional Tolerance • It ain’t gonna go away

All this leads to Positional Tolerance • It ain’t gonna go away

Download this Presentation • An annotated version of this presentation with speaker’s notes is available for downloading at: http: //www. lsawnoly. org/lsitresources. html