WEEK EMT 1253 DIGITAL ELECTRONIC PRINCIPLES COMBINATIONAL LOGIC

WEEK EMT 125/3 DIGITAL ELECTRONIC PRINCIPLES COMBINATIONAL LOGIC FUNCTIONS SITI ZARINA BINTI MD NAZIRI | SCHOOL OF MICROELECTRONIC ENGINEERING | Uni. MAP

Combinational Logic Functions § Converters § Decoders § Encoders § Code Converters § Priority Encoder § Data Selectors § Multiplexers (Data Selectors) § Demultiplexers 2

WEEK EMT 125/3 DIGITAL ELECTRONIC PRINCIPLES COMBINATIONAL LOGIC FUNCTIONS CONVERTERS SITI ZARINA BINTI MD NAZIRI | SCHOOL OF MICROELECTRONIC ENGINEERING | Uni. MAP
Decoders § § A decoder is a circuit that detects the presence of a specified combination of bits (code) on its inputs and indicates of that code by a specified output level. Selects one of several output lines, based on a coded input signal. • Only one output is activated for each input code. • The output can be made active. HIGH or active-LOW. • With N inputs (2 N input codes, 2 N outputs are required) Modified 4

active-HIGH and active-LOW § Active HIGH: the signal will perform the action when it is HIGH or “ 1”. § Active LOW: the signal will perform the action when it is LOW or “ 0”. An active LOW input or output is indicated by an inversion bubble.

Decoders § Active HIGH output: Can be implemented using inverters and AND logic gates. § Active LOW output: Can be implemented using inverters and NAND logic gates. Newly added

Decoder – active-HIGH outputs Basic Binary Decoder Example: § To determine when a binary 1001 occurs on the input of a digital circuit, AND gate can be used as the basic decoding element. § AND gate -> produce HIGH output when all inputs are HIGH § How to ensure that inputs to the AND gate are HIGH when binary 1001 occurs? Other than this input combinations, the output is 0
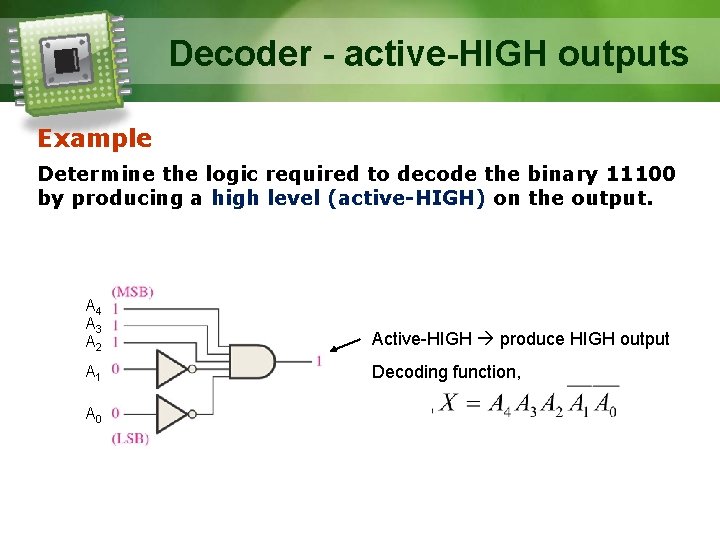
Decoder - active-HIGH outputs Example Determine the logic required to decode the binary 11100 by producing a high level (active-HIGH) on the output. A 4 A 3 A 2 Active-HIGH produce HIGH output A 1 Decoding function, A 0
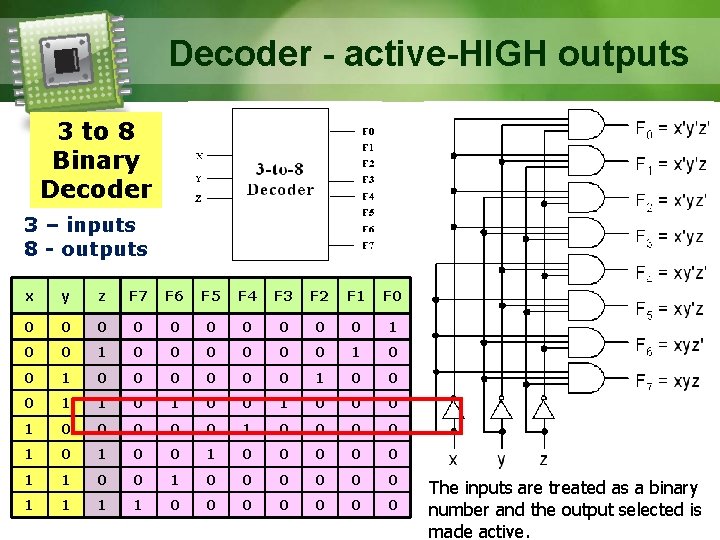
Decoder - active-HIGH outputs 3 to 8 Binary Decoder 3 – inputs 8 - outputs x y z F 7 F 6 F 5 F 4 F 3 F 2 F 1 F 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 1 0 0 0 0 The inputs are treated as a binary number and the output selected is made active.

Decoder - active-LOW outputs 4 -line-to-16 -line Decoder (4 -bit decoder) 4 – inputs 16 - outputs v. The 4 -line-to-16 -line BIN/DEC decoder in the figure is an example of a decoder with active LOW outputs. Do you notice the bubbles at the outputs? v. The entire decoder can be implemented with NAND gates and inverters. Draw the truth-table for this decoder 10

Decoder - active-LOW outputs The BCD to Decimal Decoder Are the outputs of this decoder active-HIGH or active-LOW? 11
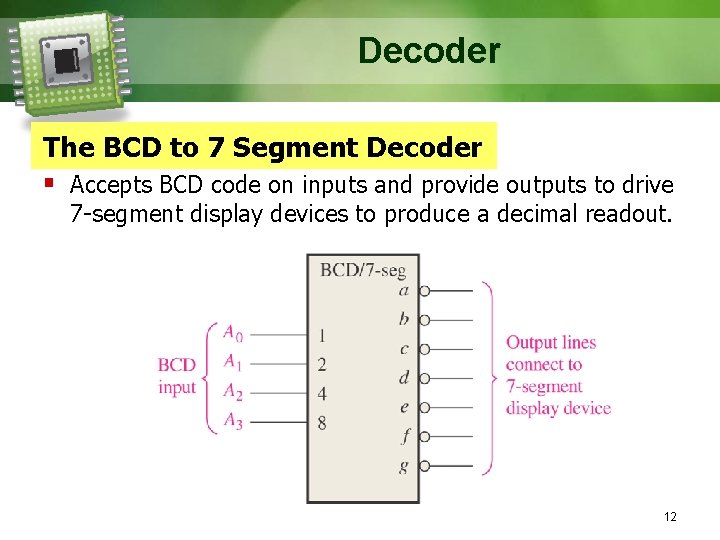
Decoder The BCD to 7 Segment Decoder § Accepts BCD code on inputs and provide outputs to drive 7 -segment display devices to produce a decimal readout. 12

Decoder Seven Segment Decoder - A seven segment decoder has seven segment display as follows: Seven-segment display format showing arrangement of segments. Display of decimal digits with a 7 -segment device. 13
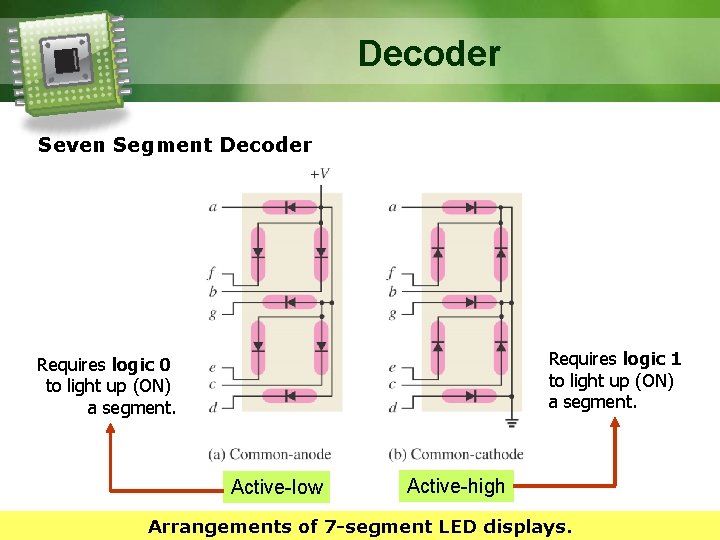
Decoder Seven Segment Decoder Requires logic 1 to light up (ON) a segment. Requires logic 0 to light up (ON) a segment. Active-low Active-high Arrangements of 7 -segment LED displays.
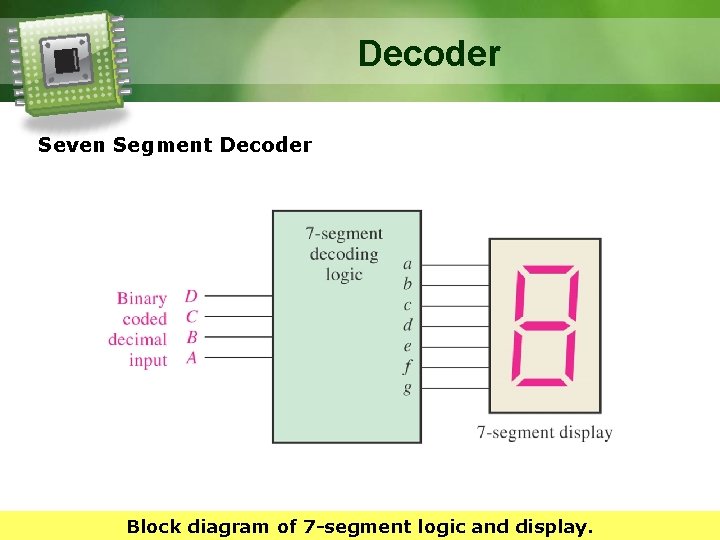
Decoder Seven Segment Decoder Block diagram of 7 -segment logic and display.

Decoder Example: § The figure above shows the -- don’t care inputs -- § numbers that will be displayed on the seven segment. Assume the seven segment has a common cathode (active-HIGH inputs). DC 0 0 0 0 0 1 0 1 1 1 1 1 B A 0 0 0 1 1 0 1 1 a 1 0 1 1 1 x x x b 1 1 1 0 0 1 1 1 x x x c 1 1 0 1 1 1 1 x x x d e f 1 1 1 0 0 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 x x x x x g 0 0 1 1 1 0 1 1 x x x

Decoder Example: § The figure above shows the -- don’t care inputs -- § numbers that will be displayed on the seven segment. Assume the seven segment has a common anode (active-LOW inputs). DC 0 0 0 0 0 1 0 1 1 1 1 1 B A 0 0 0 1 1 0 1 1 a 0 1 0 0 0 x x x b 0 0 0 1 1 0 0 0 x x x c 0 0 1 0 0 0 0 x x x d e f 0 0 0 1 1 1 1 0 0 0 0 1 1 1 0 0 0 1 1 0 x x x x x g 1 1 0 0 0 1 0 0 x x x

Design Example From the truth table, an SOP or POS can be written for each segment. § Derive an SOP for segment a. § Minimize the SOP using a K-map. § Draw the logic circuit to implement segment a of the 7 -segment display. 18
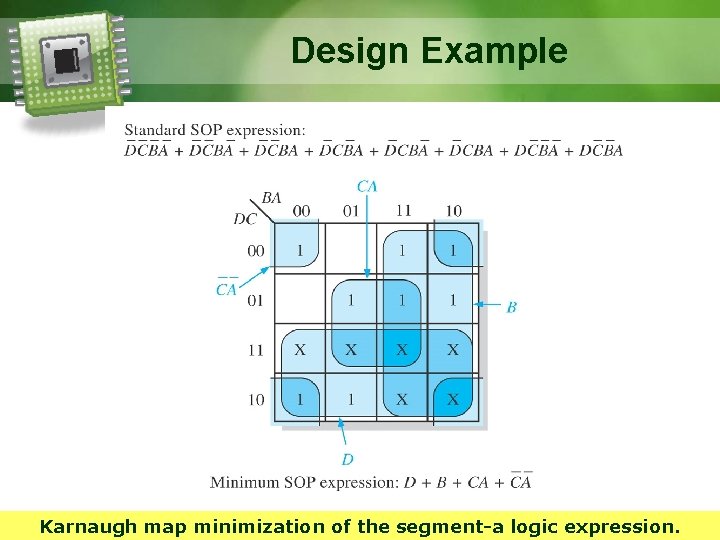
Design Example Karnaugh map minimization of the segment-a logic expression.
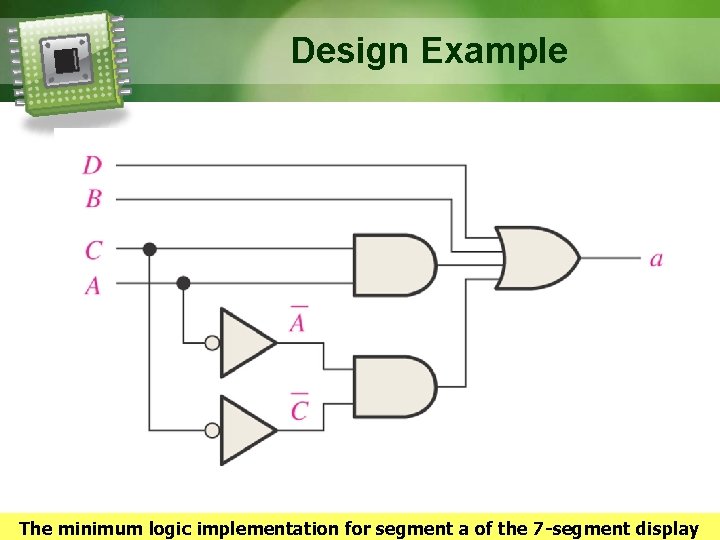
Design Example The minimum logic implementation for segment a of the 7 -segment display

Decoders – Function Implementation Example: Implementing a Binary Adder Using a Decoder For a full adder, the addition of X, Y, and C-in result in the sum (S) and carry out bit (C-out) expression are as follows: Inputs S(X, Y, C-in) = m (1, 2, 4, 7) C-out(X, Y, C-in) = m (3, 5, 6, 7) So, there are 3 inputs and 8 minterms Use a 3 -to-8 decoder. A 0 0 1 1 B C-in 0 0 0 1 1 Outputs S C-out 0 0 1 1 0 0 1 1 1
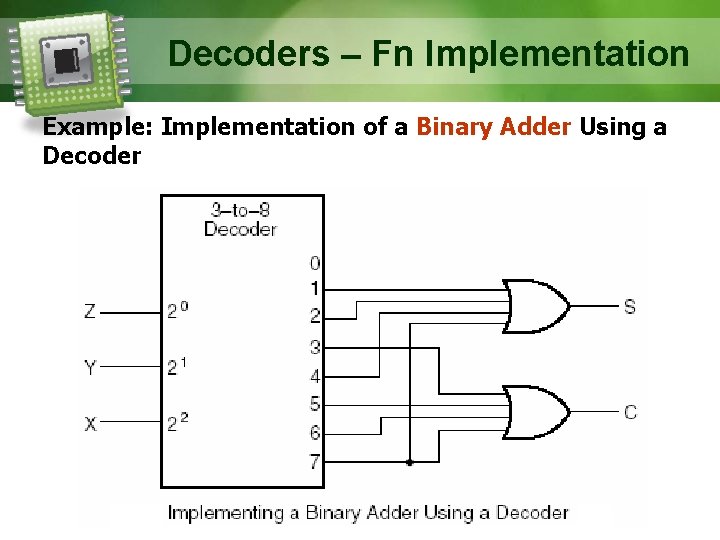
Decoders – Fn Implementation Example: Implementation of a Binary Adder Using a Decoder

Decoder with enable input § Example: 2 -to-4 decoder with enable input (E). Assume all inputs and outputs are active-HIGH. Truth table Inputs Outputs E A 1 A 0 Y 3 Y 2 Y 1 Y 0 0 X X 0 0 1 0 0 0 1 1 0 0 1 1 0 0 0 Your task: Design the decoder Newly added

Decoders - Expansion § Expansion is needed when a certain decoder size in need, but only smaller number of sizes is available § Combine 2 or more decoders in a hierarchy, i. e. cascade the smaller decoders to form a larger decoder size.
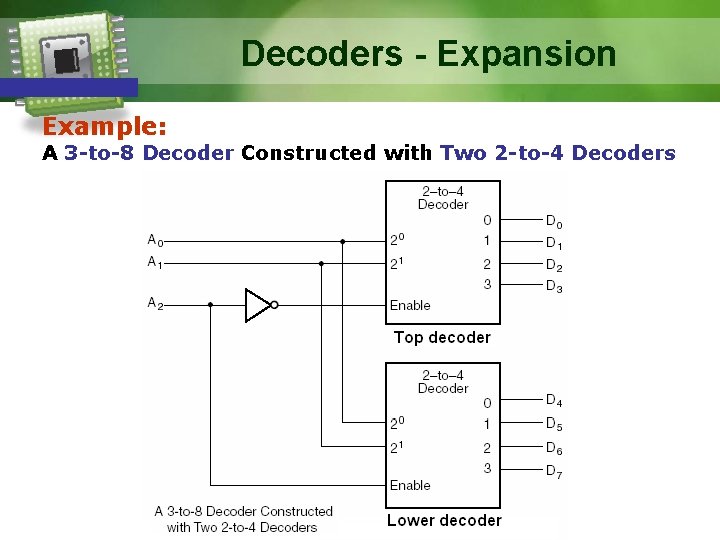
Decoders - Expansion Example: A 3 -to-8 Decoder Constructed with Two 2 -to-4 Decoders

Decoders - Expansion The Operation The MSB input, A 2, functions: § As enable, EN, of one decoder § As its complement, EN to the other decoder When A 2=0, § Top decoder enabled Generates minterms D 0 to D 3. § Lower decoder disabled Outputs equal to 0. When A 2=1, § Top decoder disabled Outputs equal to 0. § Lower decoder enabled Generates minterms D 4 to D 7.
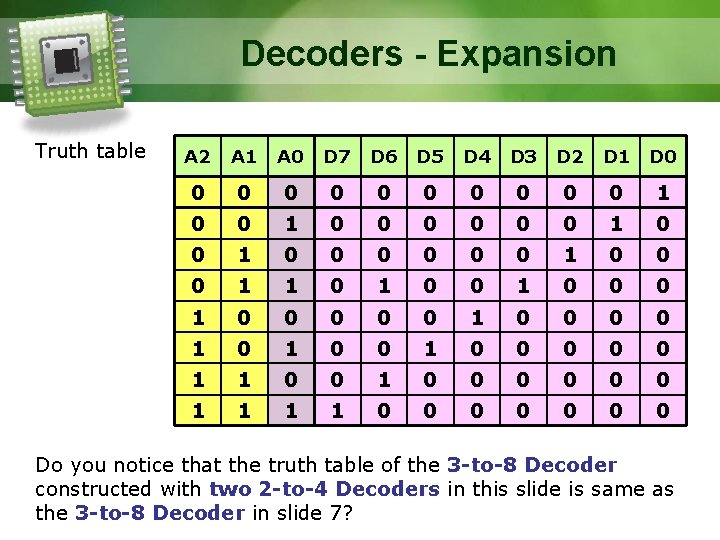
Decoders - Expansion Truth table A 2 A 1 A 0 D 7 D 6 D 5 D 4 D 3 D 2 D 1 D 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 1 0 0 0 0 Do you notice that the truth table of the 3 -to-8 Decoder constructed with two 2 -to-4 Decoders in this slide is same as the 3 -to-8 Decoder in slide 7?

Decoders - Expansion The function of EN input § Very useful and convenient way to interconnect § 2 or more functional blocks For the purpose of expanding digital functions into: § Similar functions with more inputs and outputs.

Exercise § Construct : a) a 6 -to-64 -line decoder, using: § Four 4 -to-16 -line decoders and one 2 -to-4 -line decoder. b) a 5 -to-32 -line decoder, using: § Four 3 -to-8 -line decoders and one 2 -to-4 -line decoder.

Encoder § Encoder converts information such as decimal number, alphabetical character, or symbols into some coded form, such as BCD or binary. § Performs a “reverse” decoder function. § Encoder is usually used for: § Data representation § Data security § Data compression
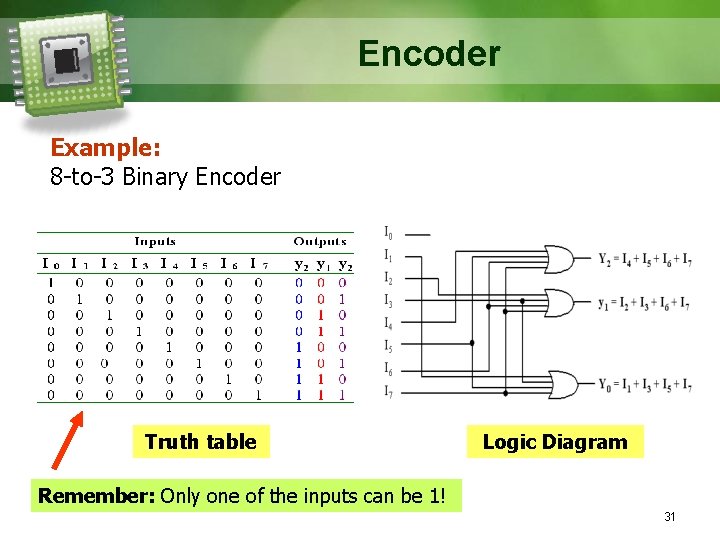
Encoder Example: 8 -to-3 Binary Encoder Truth table Logic Diagram Remember: Only one of the inputs can be 1! 31

Encoder Example Decimal to BCD Encoder Your task: DESIGN! 32

Encoder Example Design a Decimal to BCD Encoder Hints: (a) Draw a Truth-Table showing input and output - How many inputs? : 10 (0 to 9) - How many outputs? : 4 because we need 4 bits to express 9 (1001) (b) From the Truth-Table, get the equation for each output - How many Boolean expression? : 4 since there are 4 outputs (c) Based on the output equation, draw a circuit for basic decimal-to-BCD encoder
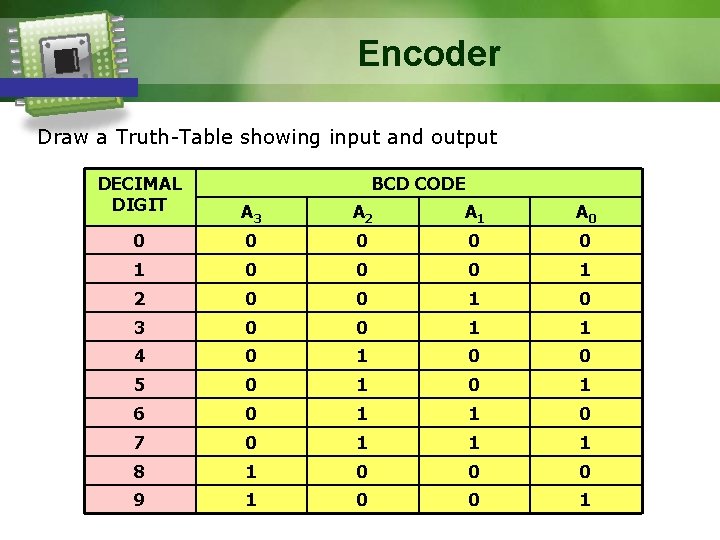
Encoder Draw a Truth-Table showing input and output DECIMAL DIGIT BCD CODE A 3 A 2 A 1 A 0 0 0 1 2 0 0 1 0 3 0 0 1 1 4 0 1 0 0 5 0 1 6 0 1 1 0 7 0 1 1 1 8 1 0 0 0 9 1 0 0 1
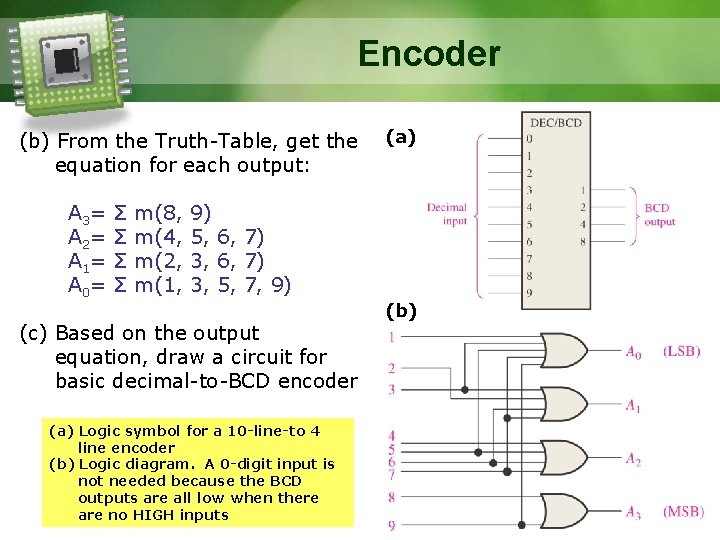
Encoder (b) From the Truth-Table, get the equation for each output: A 3= A 2= A 1= A 0= Σ Σ m(8, m(4, m(2, m(1, (a) 9) 5, 6, 7) 3, 5, 7, 9) (c) Based on the output equation, draw a circuit for basic decimal-to-BCD encoder (a) Logic symbol for a 10 -line-to 4 line encoder (b) Logic diagram. A 0 -digit input is not needed because the BCD outputs are all low when there are no HIGH inputs (b)

Encoder – Some Limitation a) If two inputs are active simultaneously, the output produces an undefined combination. For example, if input 3 and 6 are active simultaneously, the encoder will become 0111 because all three output are equal to 1. This does not represent a binary 3 or 6. To resolve this ambiguity, encoder circuits must establish a priority to ensure that only one input is encoded. b) Another ambiguity is that an output with all 0’s is generated when all inputs are 0’s. However, the output with 0’s is also generated when input 0 = 1. This ambiguity can be resolved by providing an additional output that specifies the condition that none of the inputs are active. Newly added

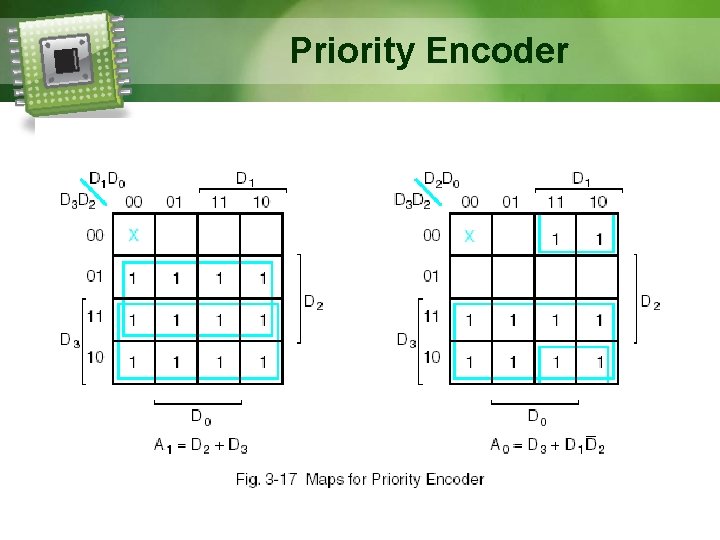
Priority Encoder (a) What about when 2 inputs are 1 at the same time? § Use “Priority Encoder” § To ensure only one input is encoded. § If 2 or more inputs are equal to 1 at the same time, the input having the highest priority is the one encoded. Example: D 3 = D 6 = 1 Output = 110 (D 6 has a higher priority than D 3) Modified 37

Priority Encoder (b) How to differentiate between inputs are all 0’s or input 0 = 1? § Use “Priority Encoder” § A valid-output indicator (V), is set to 1 when only one or more inputs are active. If all inputs are not active, V = 0. Newly added

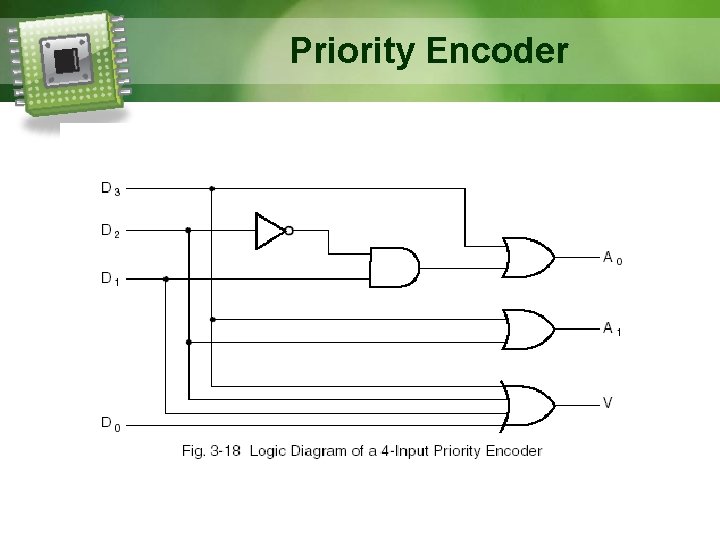
Priority Encoder • Example: 4 -input Priority Encoder § Use condensed truth table (5 rows to represent 16 rows). § V (valid) = 1 when 1 or more input is equal to 1. Modified
Priority Encoder
Priority Encoder

Code converter: BCD to binary § The basic conversion process is as follows: § The value or weight of each bit in the BCD code is represented by a binary number. § All the binary representations of the weights of the bits that are 1 s in the BCD number are added. § The result of the addition is the binary equivalent of the BCD number. 42

Code converter: BCD to binary § Example: Given a decimal number 8710. § When expressed in BCD code, 8710 = 1000 0111 § § (B 3 B 2 B 1 B 0 A 3 A 2 A 1 A 0). The leftmost 4 -bit group represents 80 and the rightmost 4 -bit group represents 7 i. e. the leftmost group has a weight of 10 and the rightmost group has a weight of 1. The BCD weight of each BCD bit in the BCD code is: Tens Digit Units Digit Weight 80 40 20 10 8 4 2 1 Bit Designation B 3 B 2 B 1 B 0 A 3 A 2 A 1 A 0 43
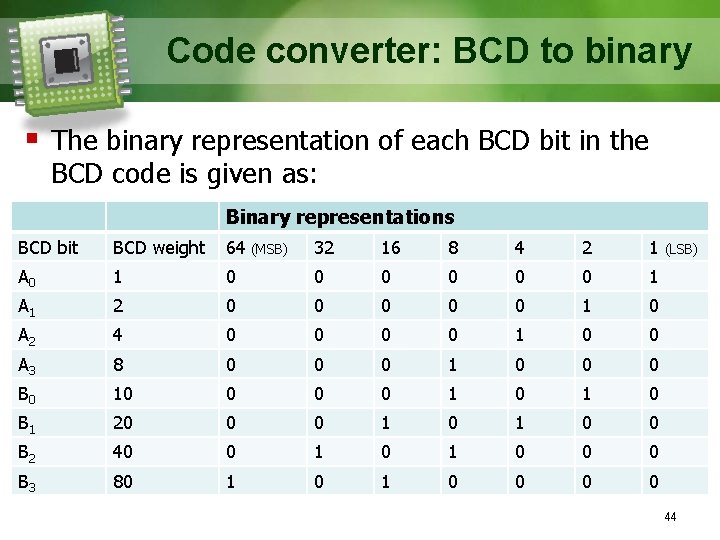
Code converter: BCD to binary § The binary representation of each BCD bit in the BCD code is given as: Binary representations BCD bit BCD weight 64 32 16 8 4 2 1 A 0 1 0 0 0 1 A 1 2 0 0 0 1 0 A 2 4 0 0 1 0 0 A 3 8 0 0 0 1 0 0 0 B 0 10 0 1 0 B 1 20 0 0 1 0 0 B 2 40 0 1 0 0 0 B 3 80 1 0 0 (MSB) (LSB) 44

Code converter: BCD to binary § By adding the binary representations for the weights of all the 1 s in the BCD code, the result is the binary representation of the BCD code. § Example: Convert BCD number 98 to binary. Tens Digit Units Digit Weight 80 40 20 10 8 4 2 1 98 1 0 0 1 1 0 0 0 1010000 0001010 0001000 1100010 1010000 0001010 0001000 Binary number for decimal 98 E D N 45
- Slides: 45