Week 5 Crystal Structure In Material Sem 2

Week 5: Crystal Structure In Material Sem 2 (2017/18) DMT 125: Materials Science

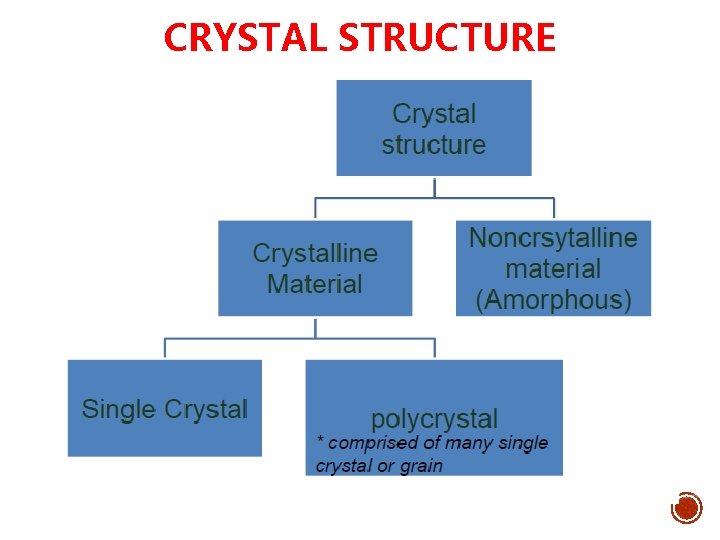
CRYSTAL STRUCTURE

MATERIALS AND PACKING Materials – Atoms/ions arrangement • Crystalline material - Material whose atoms and ions arranged in a pattern (long-range order) • Amorphous or non-crystalline - Material whose atoms and ions that are not arranged in a long range, periodic, and repeated manner (shortrange order )

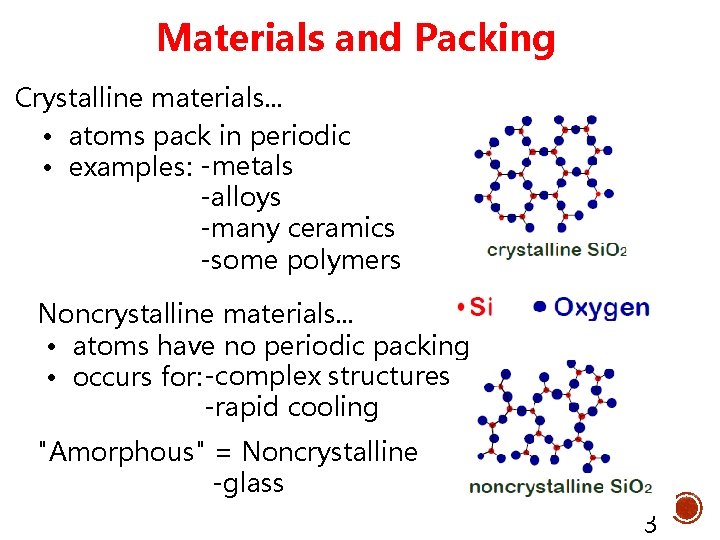
Materials and Packing Crystalline materials. . . • atoms pack in periodic • examples: -metals -alloys -many ceramics -some polymers Noncrystalline materials. . . • atoms have no periodic packing • occurs for: -complex structures -rapid cooling "Amorphous" = Noncrystalline -glass 3

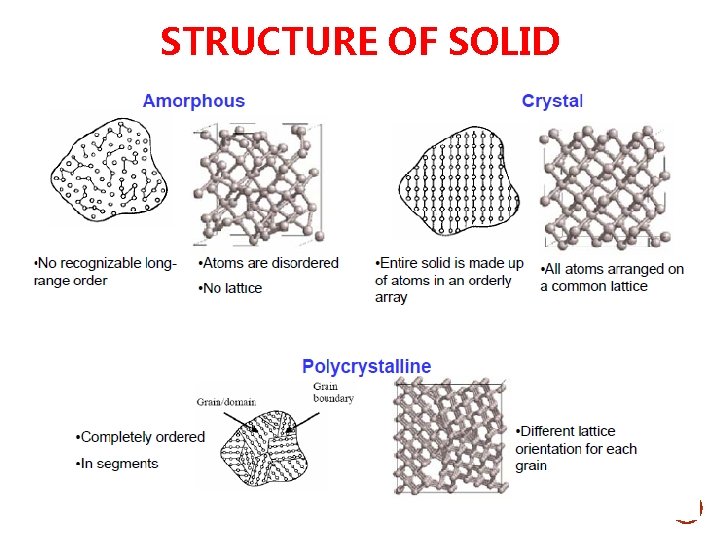
STRUCTURE OF SOLID

CRYSTALLINE STRUCTURE

AMORPHOUS Cleavage surfaces of an amorphous solid. Obsidian, a volcanic glass with the same chemical composition as granite (typically KAl. Si 3 O 8), tends to have curved, irregular surfaces when cleaved.

Amorphous solids § they have poorly defined patterns when exposed to x-rays because their components are not arranged in a regular array. § An amorphous, translucent solid is called a glass. § Almost any substance can solidify in amorphous form if the liquid phase is cooled rapidly enough. § Some solids, however, are intrinsically amorphous, because either their components cannot fit together well enough to form a stable crystalline lattice or they contain impurities that disrupt the lattice.

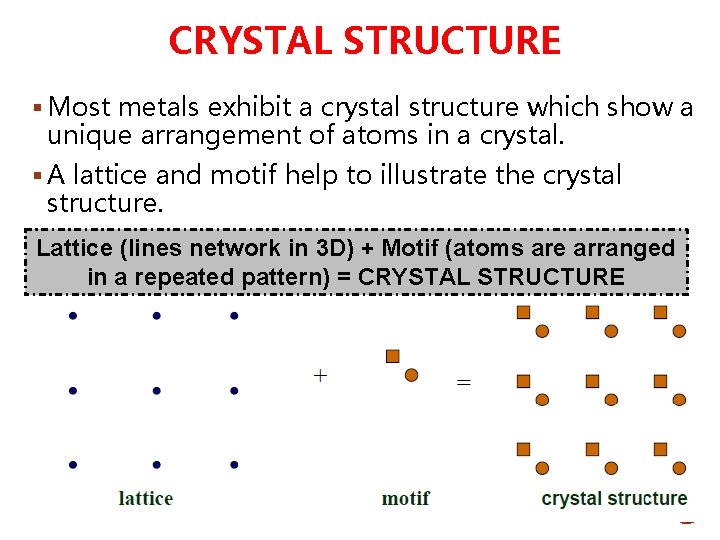
CRYSTAL STRUCTURE § Most metals exhibit a crystal structure which show a unique arrangement of atoms in a crystal. § A lattice and motif help to illustrate the crystal structure. Lattice (lines network in 3 D) + Motif (atoms are arranged in a repeated pattern) = CRYSTAL STRUCTURE

§ A crystal structure is formed when a group of atoms or molecules are attached identically to each lattice point. This group of atoms or molecules are called motif. § Motif is identical – in composition, § in arrangement, § in orientation. § and repeated periodically in space to form the crystal structure which can be represented by the logical formula: § Lattice + motif = crystal structure

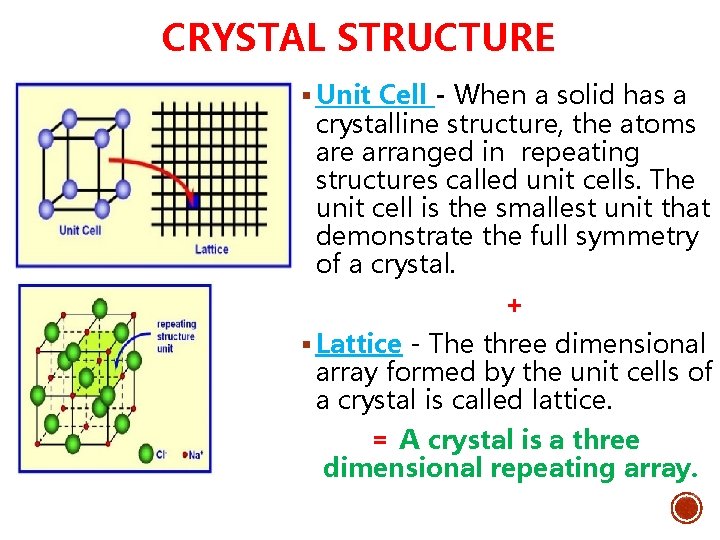
CRYSTAL STRUCTURE § Unit Cell - When a solid has a crystalline structure, the atoms are arranged in repeating structures called unit cells. The unit cell is the smallest unit that demonstrate the full symmetry of a crystal. + § Lattice - The three dimensional array formed by the unit cells of a crystal is called lattice. = A crystal is a three dimensional repeating array.

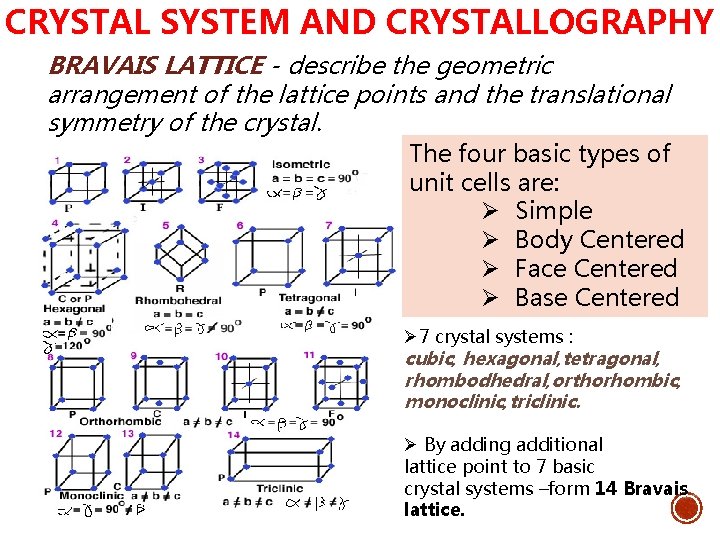
CRYSTAL SYSTEM AND CRYSTALLOGRAPHY BRAVAIS LATTICE - describe the geometric arrangement of the lattice points and the translational symmetry of the crystal. The four basic types of unit cells are: Ø Simple Ø Body Centered Ø Face Centered Ø Base Centered Ø 7 crystal systems : cubic, hexagonal, tetragonal, rhombodhedral, orthorhombic, monoclinic, triclinic. Ø By adding additional lattice point to 7 basic crystal systems –form 14 Bravais lattice.

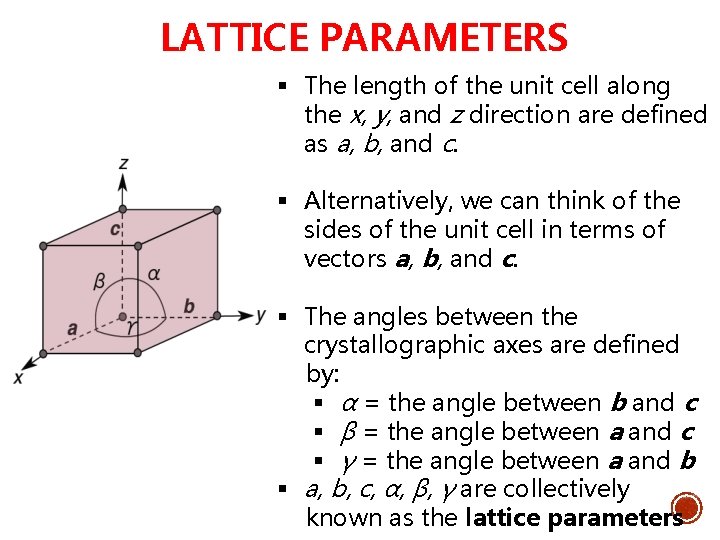
LATTICE PARAMETERS § The length of the unit cell along the x, y, and z direction are defined as a, b, and c. § Alternatively, we can think of the sides of the unit cell in terms of vectors a, b, and c. § The angles between the crystallographic axes are defined by: § α = the angle between b and c § β = the angle between a and c § γ = the angle between a and b § a, b, c, α, β, γ are collectively known as the lattice parameters

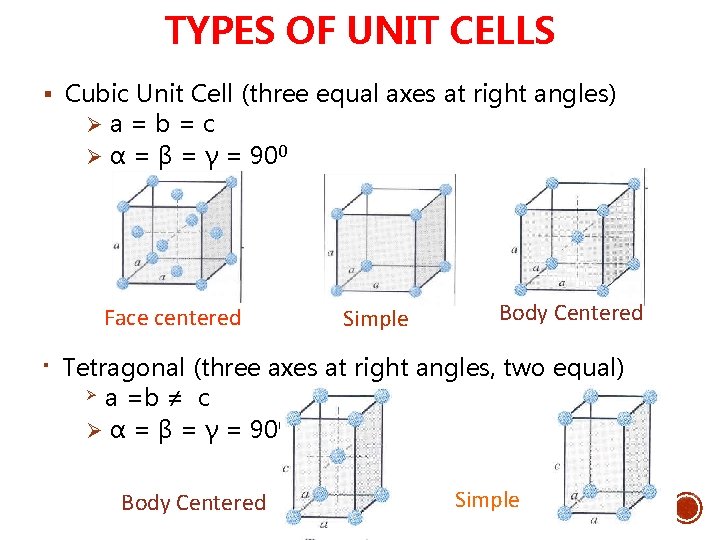
TYPES OF UNIT CELLS § Cubic Unit Cell (three equal axes at right angles) Ø a = b = c Ø α = β = γ = 900 Face centered § Simple Body Centered Tetragonal (three axes at right angles, two equal) Ø a =b ≠ c Ø α = β = γ = 900 Body Centered Simple

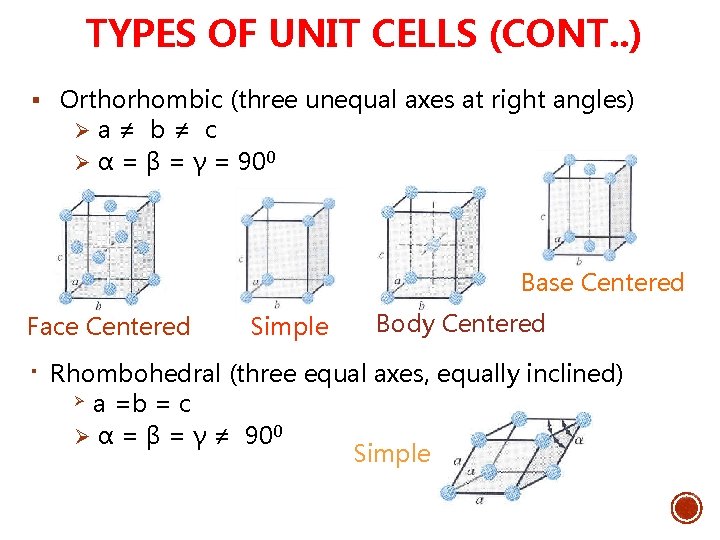
TYPES OF UNIT CELLS (CONT. . ) § Orthorhombic (three unequal axes at right angles) Ø a ≠ b ≠ c Ø α = β = γ = 900 Base Centered Face Centered § Simple Body Centered Rhombohedral (three equal axes, equally inclined) Ø a =b = c Ø α = β = γ ≠ 900 Simple

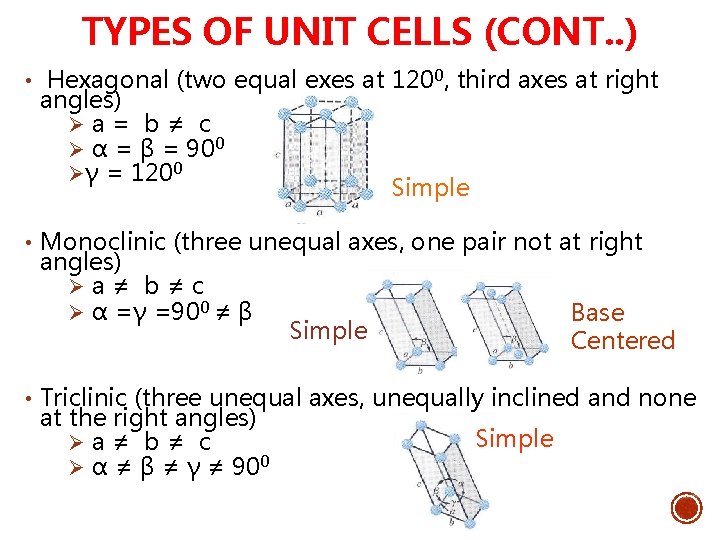
TYPES OF UNIT CELLS (CONT. . ) • Hexagonal (two equal exes at 1200, third axes at right angles) Ø a = b ≠ c Ø α = β = 900 Øγ = 1200 Simple • Monoclinic (three unequal axes, one pair not at right angles) Ø a ≠ b ≠ c Ø α =γ =900 ≠ β Base Centered Simple • Triclinic (three unequal axes, unequally inclined and none at the right angles) Ø a ≠ b ≠ c Ø α ≠ β ≠ γ ≠ 900 Simple

PRINCIPAL METALLIC CRYSTAL STRUCTURES § 90% of the metals have either Body Centered Cubic (BCC), Face Centered Cubic (FCC) or Hexagonal Close Packed (HCP) crystal structure. § HCP is denser version of simple hexagonal crystal structure. § Most metals crystallize in these dense-packed structures because energy is released (more stable) as the atoms come closer together and bond more tightly with each other.

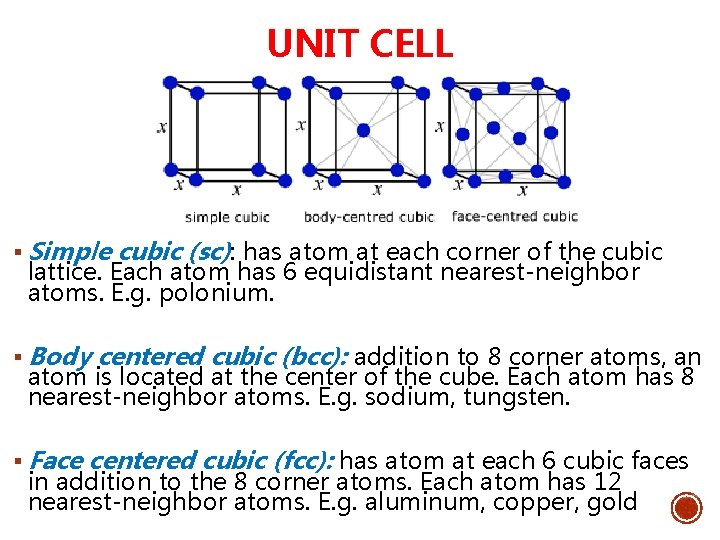
UNIT CELL § Simple cubic (sc): has atom at each corner of the cubic lattice. Each atom has 6 equidistant nearest-neighbor atoms. E. g. polonium. § Body centered cubic (bcc): addition to 8 corner atoms, an atom is located at the center of the cube. Each atom has 8 nearest-neighbor atoms. E. g. sodium, tungsten. § Face centered cubic (fcc): has atom at each 6 cubic faces in addition to the 8 corner atoms. Each atom has 12 nearest-neighbor atoms. E. g. aluminum, copper, gold

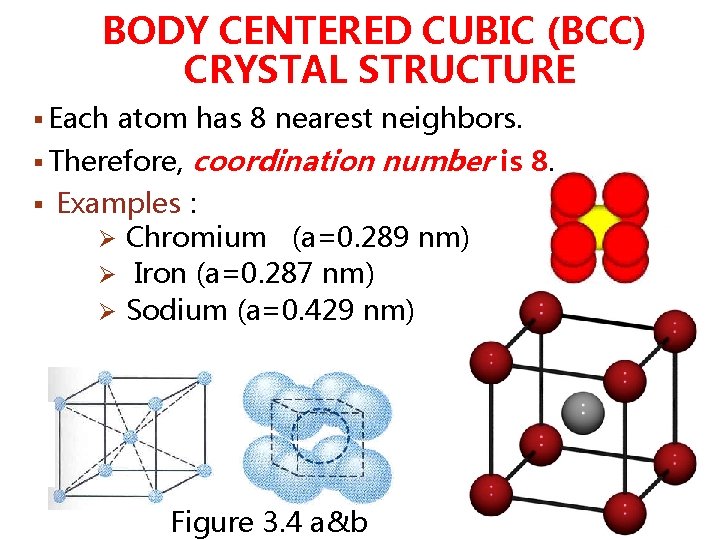
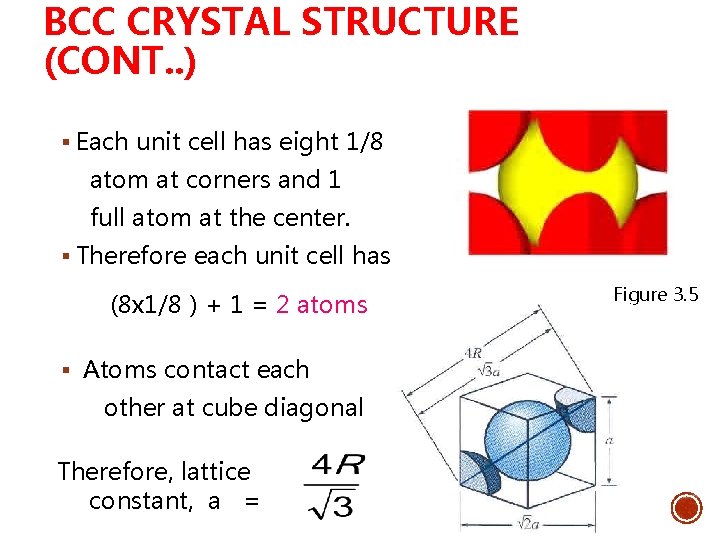
BODY CENTERED CUBIC (BCC) CRYSTAL STRUCTURE § Each atom has 8 nearest neighbors. § Therefore, coordination number is 8. § Examples : Ø Chromium (a=0. 289 nm) Ø Iron (a=0. 287 nm) Ø Sodium (a=0. 429 nm) Figure 3. 4 a&b

BCC CRYSTAL STRUCTURE (CONT. . ) § Each unit cell has eight 1/8 atom at corners and 1 full atom at the center. § Therefore each unit cell has (8 x 1/8 ) + 1 = 2 atoms § Atoms contact each other at cube diagonal Therefore, lattice constant, a = Figure 3. 5

EXAMPLE: § Iron at 20 C is BCC with atoms of atomic radius 0. 124 nm. Calculate the lattice constant, a, for the cube edge of the iron unit cell. Solutions: From Fig. 3. 5, it is seen that the atoms in the BCC unit cell touch across the cube diagonals. Thus, if a is the length of the cube edge, then

EXERCISE: § Molybdenum at 20 C is BCC and has atomic radius of 0. 140 nm. Calculate a value for its lattice constant, a, in nanometers.

ATOMIC PACKING FACTOR (APF) OF BCC STRUCTURE If the atoms in the BCC unit cell are considered to be spherical, Volume of atoms in unit cell Atomic Packing Factor = Volume of unit cell (APF) Vatoms = = 8. 373 R 3 V unit cell = a 3 = = 12. 32 R 3 3 8. 723 R Therefore APF = 12. 32 R 3 = 0. 68

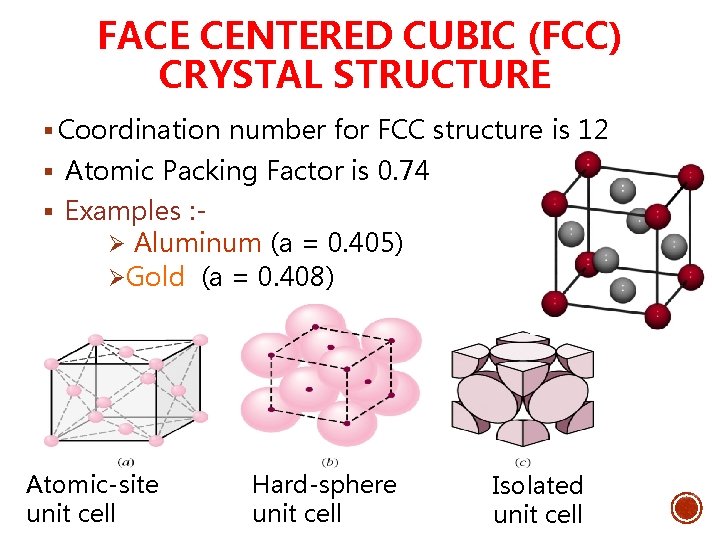
FACE CENTERED CUBIC (FCC) CRYSTAL STRUCTURE § Coordination number for FCC structure is 12 § Atomic Packing Factor is 0. 74 § Examples : Ø Aluminum (a = 0. 405) ØGold (a = 0. 408) Atomic-site unit cell Hard-sphere unit cell Isolated unit cell

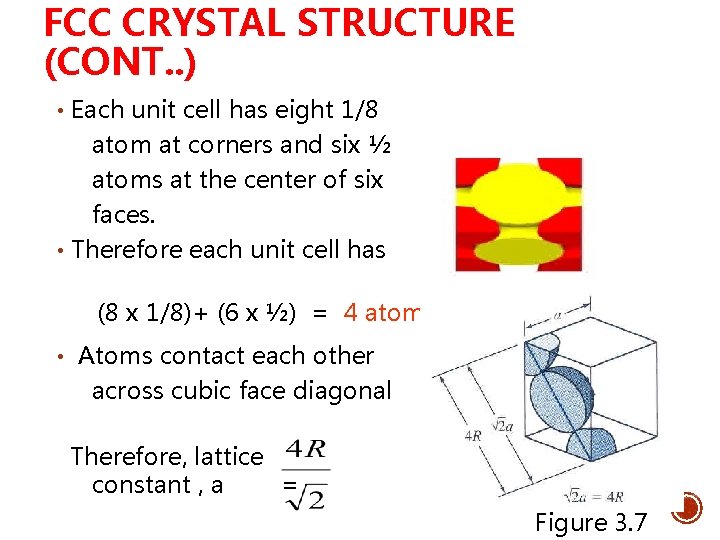
FCC CRYSTAL STRUCTURE (CONT. . ) • Each unit cell has eight 1/8 atom at corners and six ½ atoms at the center of six faces. • Therefore each unit cell has (8 x 1/8)+ (6 x ½) = 4 atoms • Atoms contact each other across cubic face diagonal Therefore, lattice constant , a = Figure 3. 7

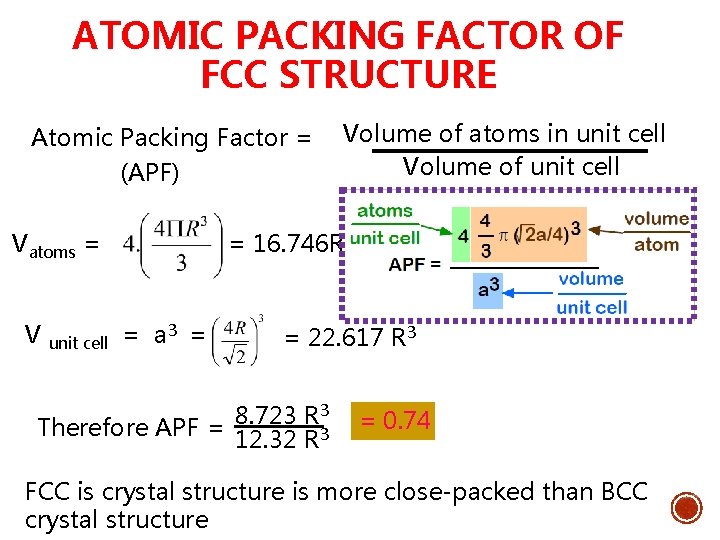
ATOMIC PACKING FACTOR OF FCC STRUCTURE Atomic Packing Factor = Volume of atoms in unit cell Volume of unit cell (APF) Vatoms = = 16. 746 R 3 V unit cell = a 3 = = 22. 617 R 3 3 8. 723 R Therefore APF = 12. 32 R 3 = 0. 74 FCC is crystal structure is more close-packed than BCC crystal structure

EXERCISE: § Gold is FCC and has a lattice constant of 0. 40788 nm. Calculate a value for the atomic radius of a gold in nanometers.

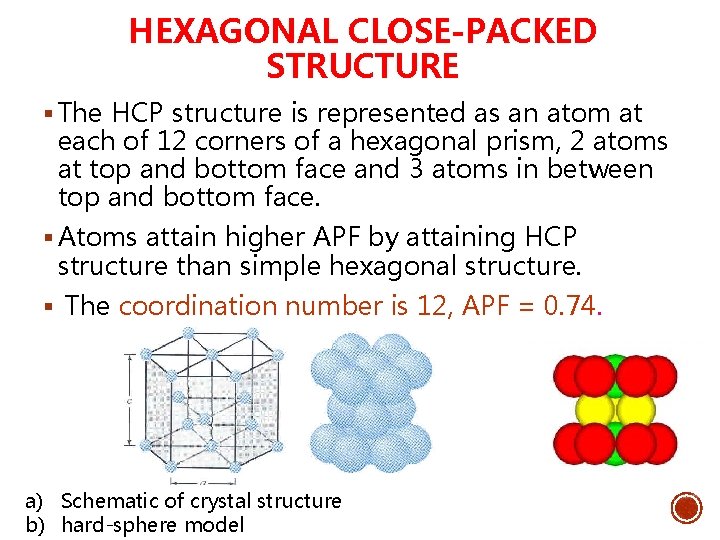
HEXAGONAL CLOSE-PACKED STRUCTURE § The HCP structure is represented as an atom at each of 12 corners of a hexagonal prism, 2 atoms at top and bottom face and 3 atoms in between top and bottom face. § Atoms attain higher APF by attaining HCP structure than simple hexagonal structure. § The coordination number is 12, APF = 0. 74. a) Schematic of crystal structure b) hard-sphere model

HCP CRYSTAL STRUCTURE (CONT. . ) § Each atom has six 1/6 atoms at each of top and bottom layer, two half atoms at top and bottom layer and 3 full atoms at the middle layer. § Therefore each HCP unit cell has (2 x 6 x 1/6) + (2 x ½) + 3 = 6 atoms § Examples: - Ø Zinc (a = 0. 2665 nm, c/a = 1. 85) Ø Cobalt (a = 0. 2507 nm, c/a = 1. 62) c § Ideal c/a ratio is 1. 633. a Figure 3. 8 c

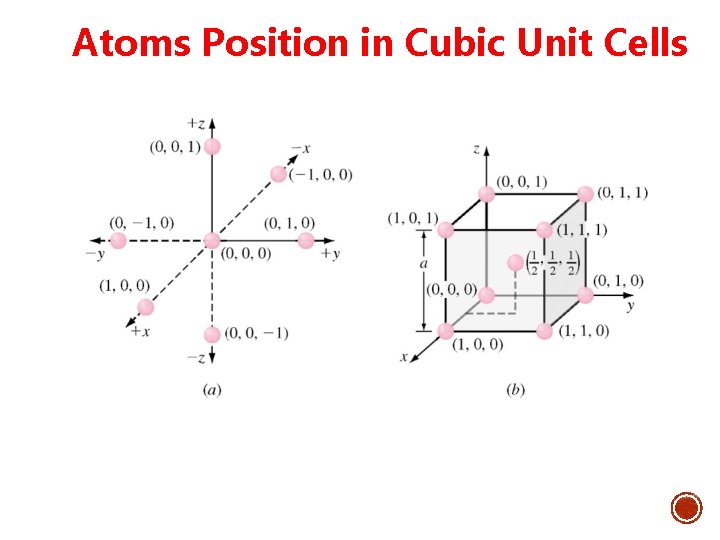
ATOM POSITIONS IN CUBIC UNIT CELLS § Cartesian coordinate system is use to locate atoms. § In a cubic unit cell Ø y axis is the direction to the right. Ø x axis is the direction coming out of the paper. Ø z axis is the direction towards top. Ø Negative directions are to the opposite of positive directions. • Atom positions in unit cells are located by using unit distances along the x, y and z axes.

Atoms Position in Cubic Unit Cells

DIRECTIONS IN CUBIC UNIT CELLS § In cubic crystals, Direction Indices are vector components of directions resolved along each axes, resolved to smallest integers. § Direction indices are position coordinates of unit cell where the direction vector emerges from cell surface, converted to integers. § The Direction Indices are enclosed by square brackets with no separating commas. Figure 3. 11

TWO IMPORTANT THINGS TO REMEMBER FOR DIRECTION INDICES…… § Note that all parallel direction vectors have the same direction indices. § Directions are said to be crystallographical equivalent if the atom spacing along each direction is the same. Example: [100], [010], [001], [100]=<100> Equivalent directions are called indices of family or form.

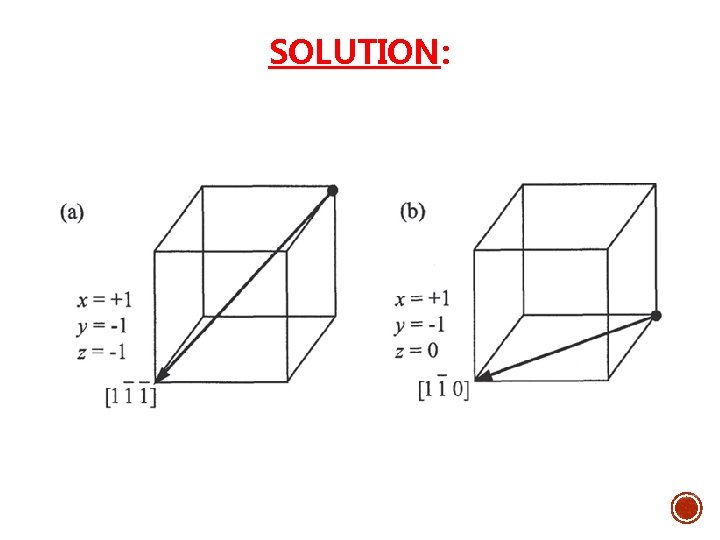
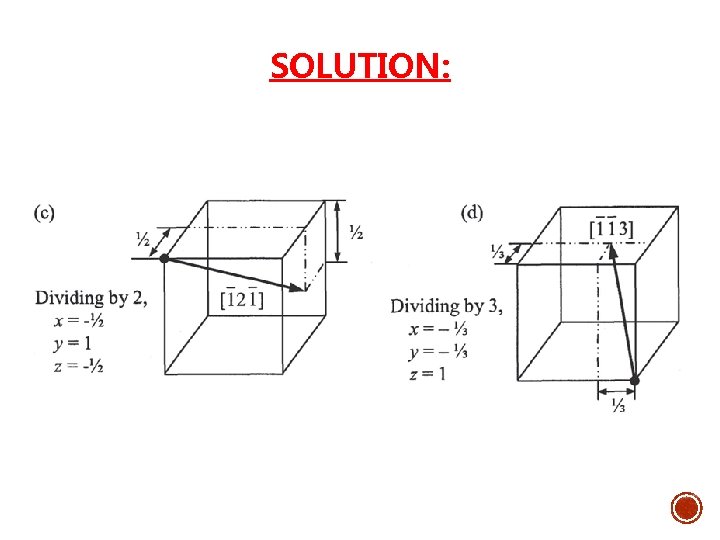
Example: 1. Draw the following direction vectors in cubic unit cells. a)[100] and [110] b) [112] c) [110] d) [321] 2. Draw directions vectors in unit cells for the following cubic directions:

Solution:

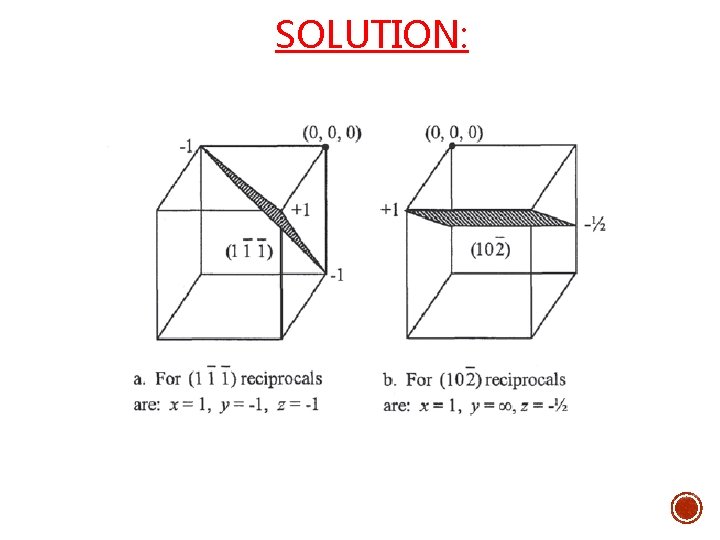
SOLUTION:

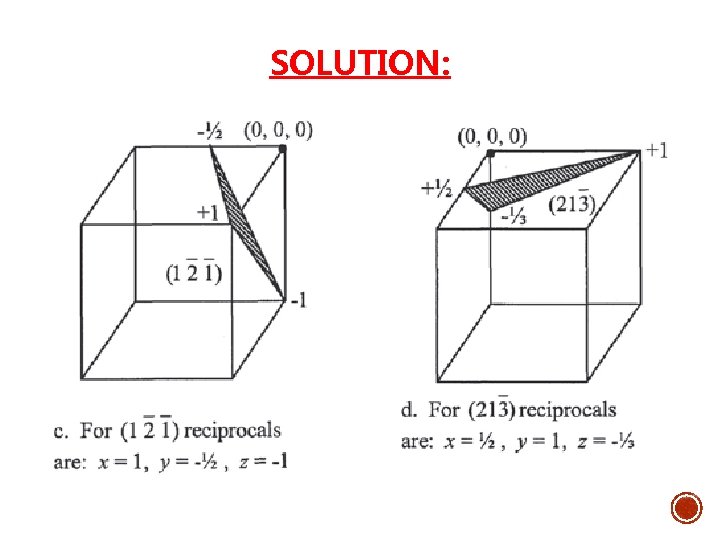
SOLUTION:

DIRECTION INDICES – EXAMPLE: § Determine direction indices of the given vector. Origin coordinates are (3/4 , 0 , 1/4). Emergence coordinates are (1/4, 1/2). Subtracting origin coordinates from emergence coordinates, (3/4 , 0 , 1/4) - (1/4, 1/2) = (-1/2, 1/4) Multiply by 4 to convert all fractions to integers 4 x (-1/2, 1/4) = (-2, 2, 1) Therefore, the direction indices are

EXERCISE: 1. A direction vector passes through a unit cube from the (3/4, 0, 1/4) to the (1/2, 1, 0) positions. What are its directions indices. Answer:

MILLER INDICES FOR CRYSTALLOGRAPHIC PLANES § Miller Indices are used to refer to specific lattice planes of atoms. § They are reciprocals of the fractional intercepts (with fractions cleared) that the plane makes with the crystallographic x, y and z axes of three nonparallel edges of the cubic unit cell. z Miller Indices =(111) y x

MILLER INDICES - PROCEDURE Choose a plane that does not pass through origin Determine the x, y and z intercepts of the plane Find the reciprocals of the intercepts Fractions? Place a ‘bar’ over the Negative indices Clear fractions by multiplying by an integer to determine smallest set of whole numbers Enclose in parenthesis (hkl)where h, k, l are miller indices of cubic crystal plane forx, y and z axes. Eg: (111)

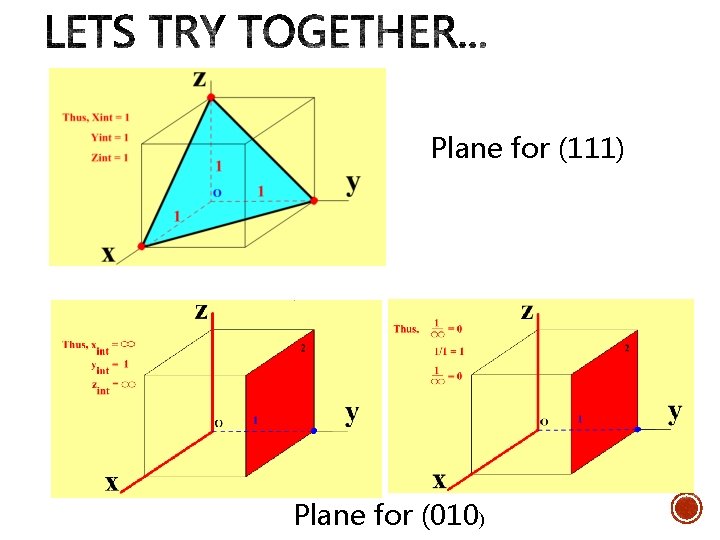
Plane for (111) Plane for (010)

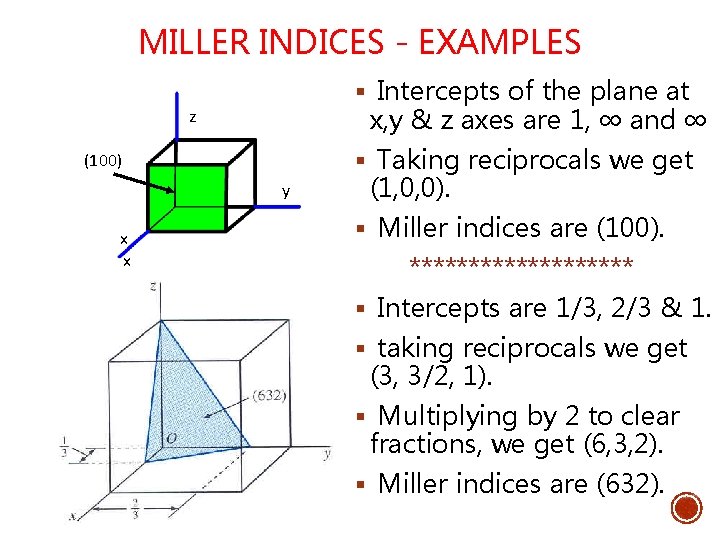
MILLER INDICES - EXAMPLES § Intercepts of the plane at x, y & z axes are 1, ∞ and ∞ z § Taking reciprocals we get (100) y x x (1, 0, 0). § Miller indices are (100). ********** § Intercepts are 1/3, 2/3 & 1. § taking reciprocals we get (3, 3/2, 1). § Multiplying by 2 to clear fractions, we get (6, 3, 2). § Miller indices are (632).

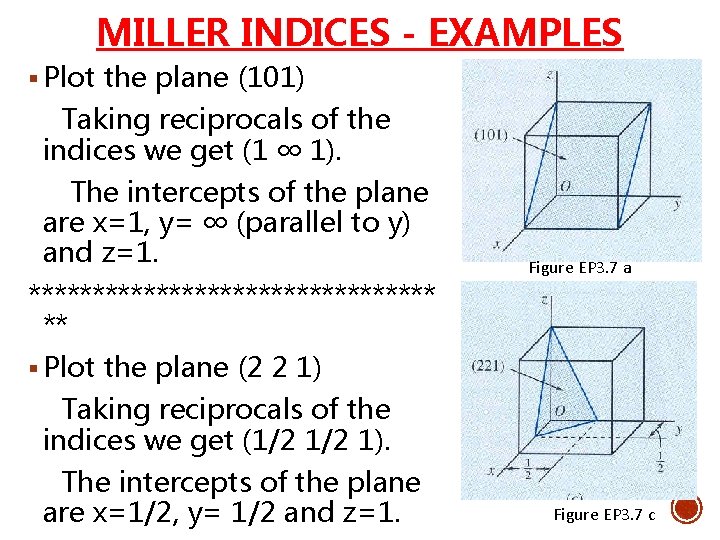
MILLER INDICES - EXAMPLES § Plot the plane (101) Taking reciprocals of the indices we get (1 ∞ 1). The intercepts of the plane are x=1, y= ∞ (parallel to y) and z=1. **************** ** Figure EP 3. 7 a § Plot the plane (2 2 1) Taking reciprocals of the indices we get (1/2 1). The intercepts of the plane are x=1/2, y= 1/2 and z=1. Figure EP 3. 7 c

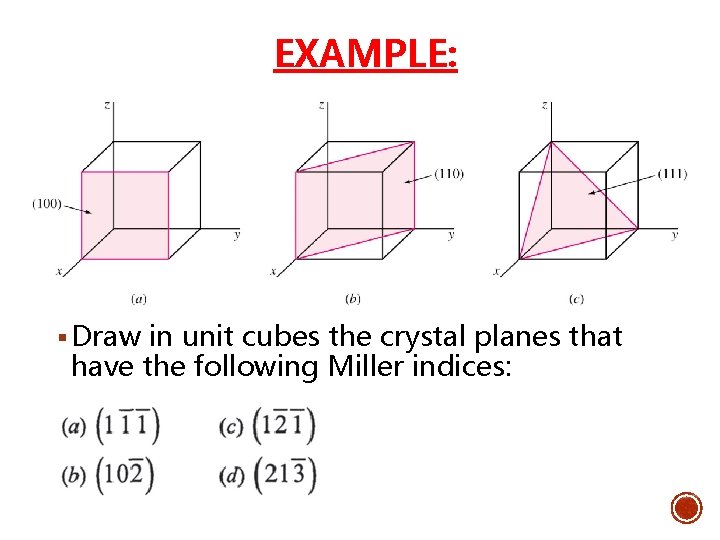
EXAMPLE: § Draw in unit cubes the crystal planes that have the following Miller indices:

SOLUTION:

SOLUTION: