Week 3 1 Week 3 2 NORMAL DISTRIBUTION

Week 3. 1

Week 3. 2

NORMAL DISTRIBUTION BERNOULLI TRIALS BINOMIAL DISTRIBUTION EXPONENTIAL DISTRIBUTION UNIFORM DISTRIBUTION POISSON DISTRIBUTION 3

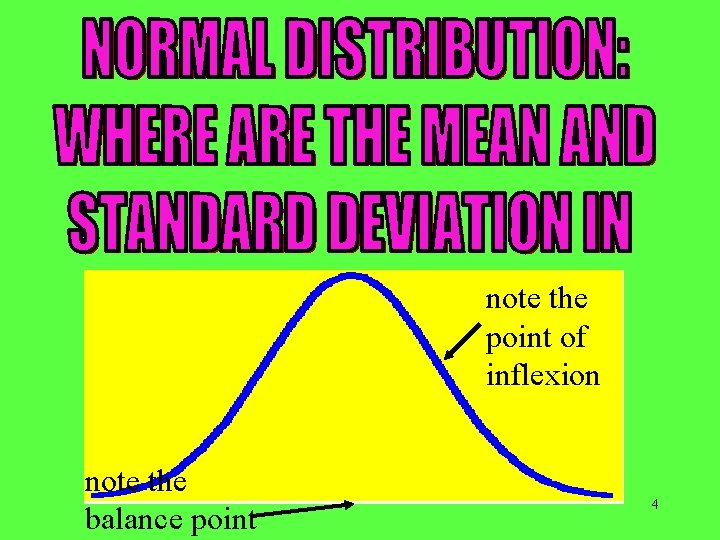
note the point of inflexion note the balance point 4

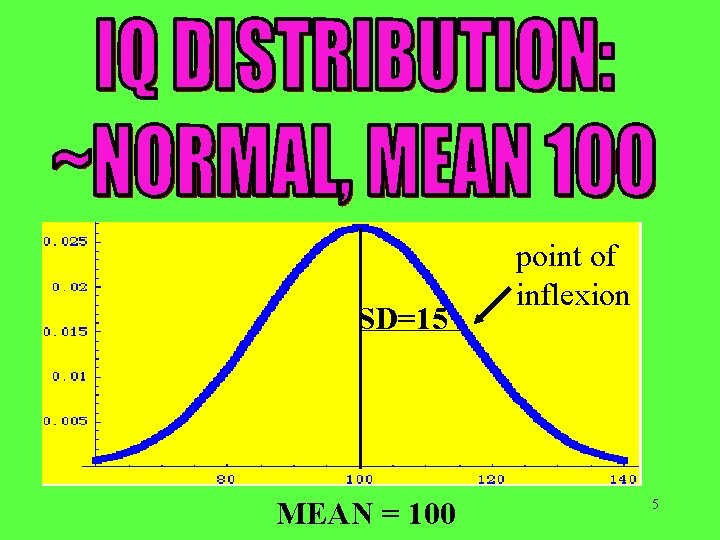
SD=15 MEAN = 100 point of inflexion 5

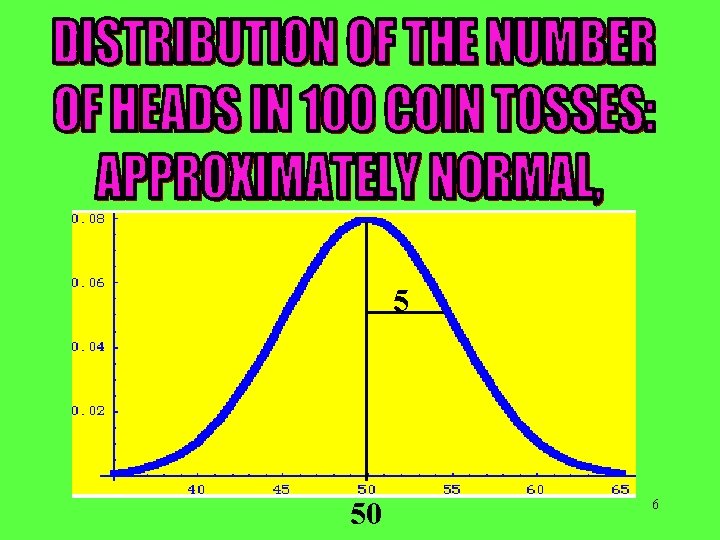
5 50 6

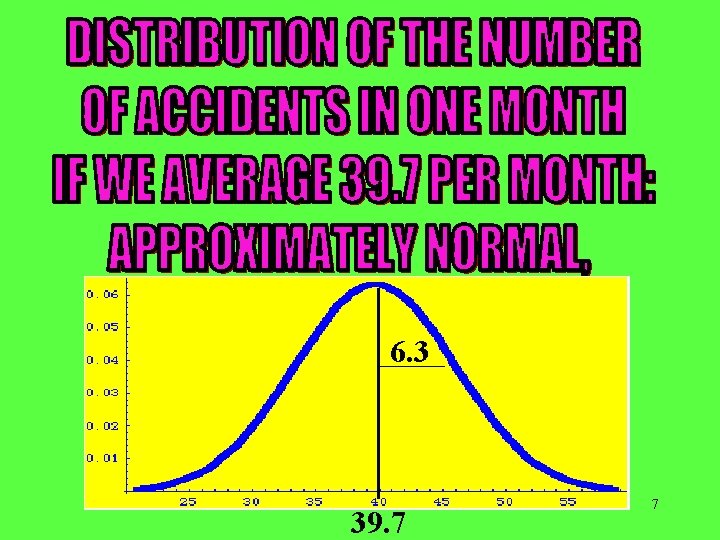
6. 3 39. 7 7

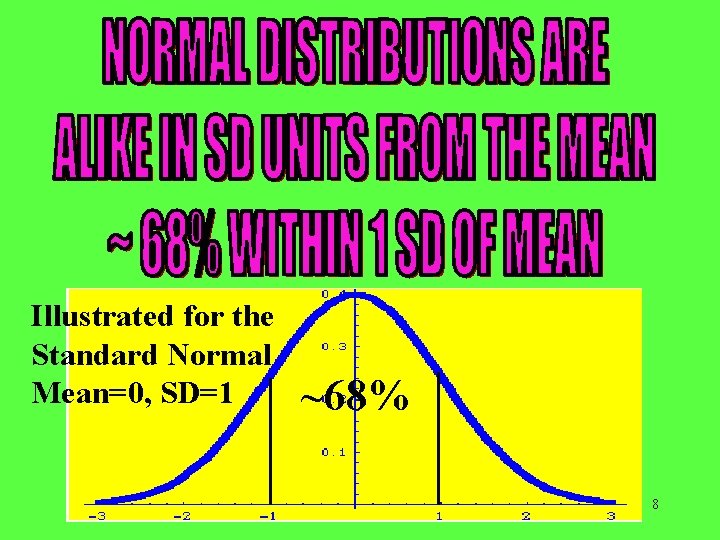
Illustrated for the Standard Normal Mean=0, SD=1 ~68% 8

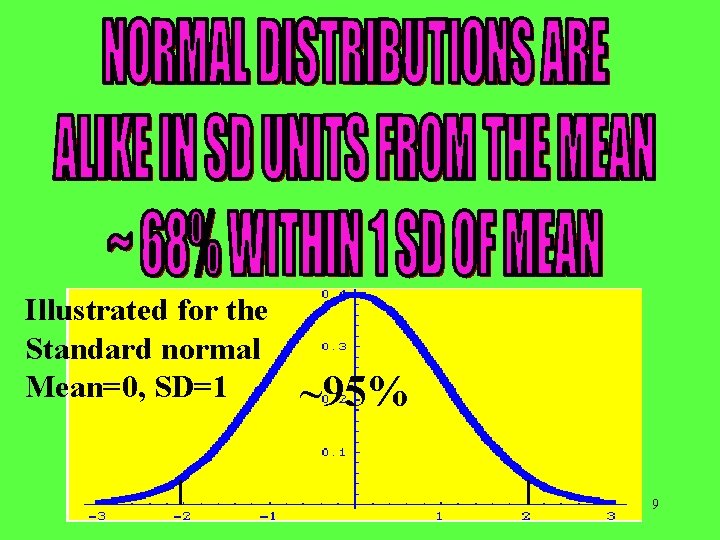
Illustrated for the Standard normal Mean=0, SD=1 ~95% 9

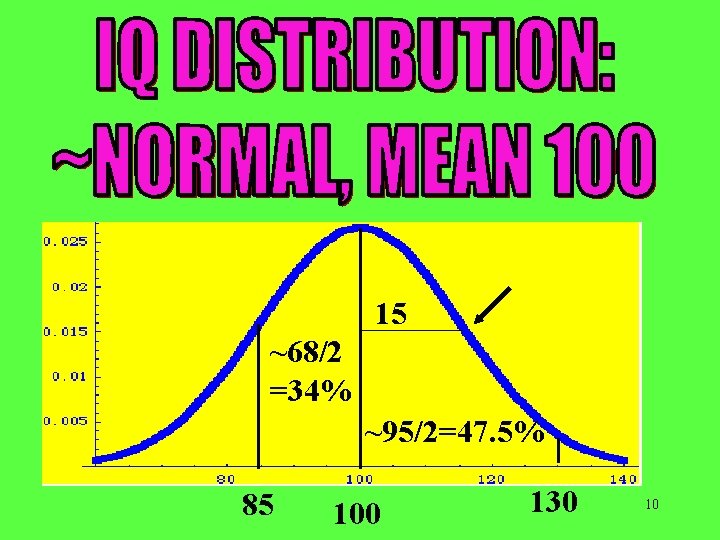
15 ~68/2 =34% ~95/2=47. 5% 85 100 130 10

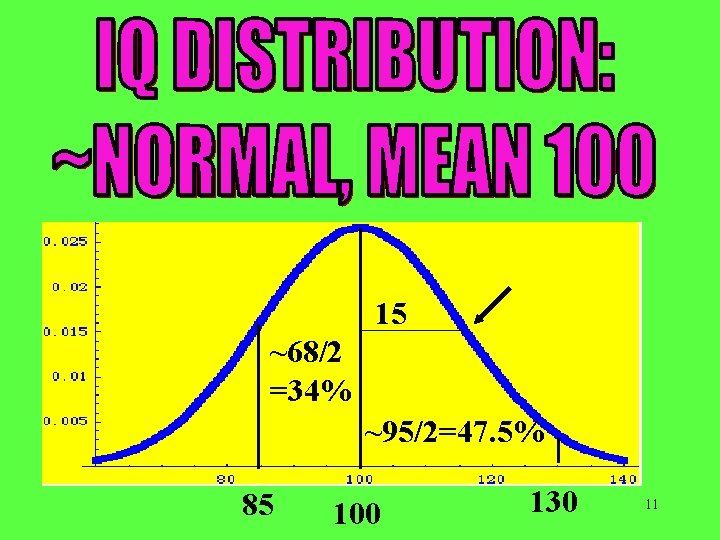
15 ~68/2 =34% ~95/2=47. 5% 85 100 130 11

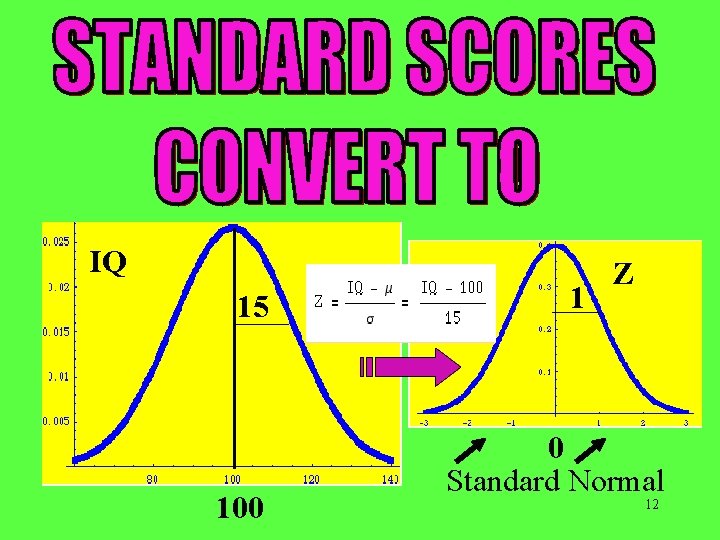
IQ 15 100 1 Z 0 Standard Normal 12

13

P(Z > 0) = P(Z < 0 ) = 0. 5 P(Z > 2. 66) = 0. 5 - P(0 < Z < 2. 66) = 0. 5 - 0. 4961 = 0. 0039 P(Z < 1. 92) = 0. 5 + P(0 < Z < 1. 92) = 0. 5 + 0. 4726 = 0. 9726 14

x 1 2 0 3 4 p(x) p (1 denotes “success”) q (0 denotes “failure”) __ 1 5 0<p<1 6 q=1 -p 15

P(success) = P(X = 1) = p P(failure) = P(X = 0) = q e. g. X = “sample voter is Democrat” Population has 48% Dem. p = 0. 48, q = 0. 52 P(X = 1) = 0. 48 16

P(S 1 S 2 F 3 F 4 F 5 F 6 S 7) = p 3 q 4 just write P(SSFFFFS) = p 3 q 4 “the answer only depends upon how many of each, not their order. ” e. g. 48% Dem, 5 sampled, with-repl: P(Dem Rep) = 0. 483 0. 522 17

e. g. P(exactly 2 Dems out of sample of 4) = P(DDRR) + P(DRDR) + P(DDRR) + P(RDDR) + P(RDRD) + P(RRDD) = 6. 482 0. 522 ~ 0. 374. There are 6 ways to arrange 2 D 2 R. 18

e. g. P(exactly 3 Dems out of sample of 5) = P(DDDRR) + P(DDRDR) + P(DDRRD) + P(DRDDR) + P(DRDRD) + P(DRRDD) + P(RDDDR) +P(RDDRD) + P(RDRDD) + P(RRDDD) = 10. 483 0. 522 ~ 0. 299. There are 10 ways to arrange 3 D 2 R. Same as the number of ways to select 3 from 5. 19

5! ways to arrange 5 things in a line Do it thus (1: 1 with arrangements): select 3 of the 5 to go first in line, arrange those 3 at the head of line then arrange the remaining 2 after. 5! = (ways to select 3 from 5) 3! 2! So num ways must be 5! /( 3! 2!) = 10. 20

Let random variable X denote the number of “S” in n independent Bernoulli p-Trials. By definition, X has a Binomial Distribution and for each of x = 0, 1, 2, …, n P(X = x) = (n!/(x! (n-x)!) ) px qn-x e. g. P(44 Dems in sample of 100 voters) = (100!/(44! 56!)) 0. 4844 0. 52100 -44 = 0. 05812. 21

n!/(x! (n-x)!) is the count of how many arrangments there are of a string of x letters “S” and n-x letters “F. ” px qn-x is the shared probability of each string of x letters “S” and n-x letters “F. ” (define 0! = 1, p 0 = q 0 = 1 and the formula goes through for every one of x = 0 through n). is short for the arrangement count = 22

23