Web Data Management Bisimulation 1 In this lecture

Web Data Management Bisimulation 1

In this lecture • Semistructured data model • Graph Simulation and Bisimulation • Computing (bi)simulation Resources Adding structure to semistructured data by Buneman, Davidson, Fernandez, Suciu, in ICDT 97 Data on the Web Abiteboul, Buneman, Suciu : section 6. 4 2

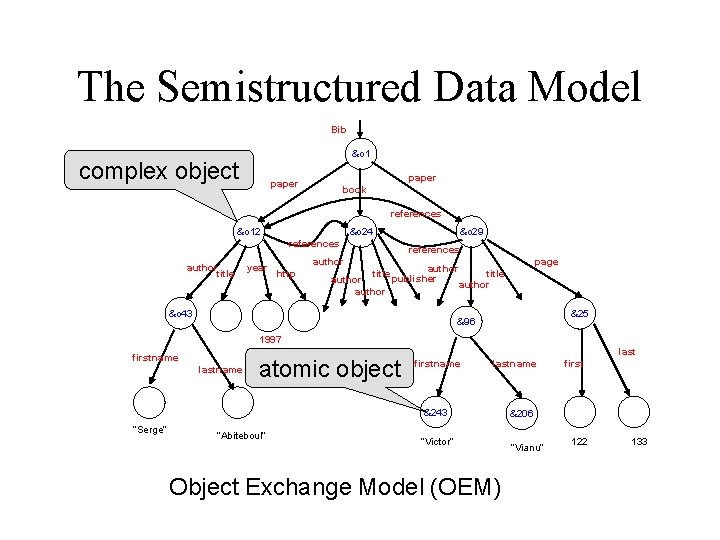
The Semistructured Data Model Bib &o 1 complex object paper book references &o 12 &o 24 &o 29 references author title year author http references author title publisher author &o 43 page title author &25 &96 1997 firstname lastname atomic object last firstname lastname &243 “Serge” “Abiteboul” “Victor” Object Exchange Model (OEM) first &206 “Vianu” 122 133 3

Syntax for Semistructured Data May omit oid’s: { paper: { author: “Abiteboul”, author: { firstname: “Victor”, lastname: “Vianu”}, title: “Regular path queries …”, page: { first: 122, last: 133 } } 4

Set Semantics for Trees Want to say that {a, a, b} = {a, b} Define equality for trees first, then for graphs Definition Two trees t, t’ are equal, t=t’, if: 1. They are both atomic values with same value 2. t = {t 1, . . . , tm}, t’ = {t 1’, . . . , tn’} and: – i=1, . . . , m, j=1, . . . , n s. t. ti = tj’ – j=1, . . . , n, i=1, . . . , m s. t. ti = tj’ 5

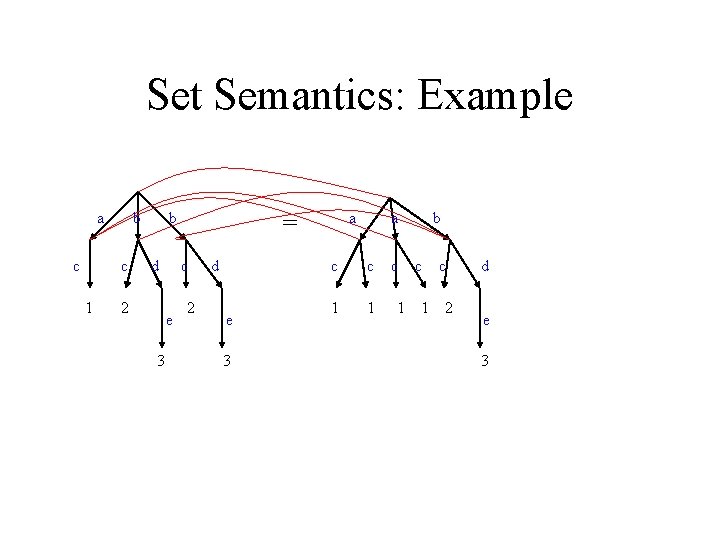
Set Semantics: Example a c b c 1 b d 2 c e 3 a = 2 d e 3 a c c 1 1 c 1 b c 1 c 2 d e 3 6

Set Semantics for Graphs • Previous definition does not apply directly to graphs with cycles • Need to adapt it bisimulation • First, we will define a simulation 7

Graph Simulation Definition Two edge-labeled graphs G 1, G 2 A simulation is a relation R between nodes: • if (x 1, x 2) R, and (x 1, a, y 1) G 1, then exists (x 2, a, y 2) G 2 (same label) s. t. (y 1, y 2) R G 1 x 1 R x 2 a a y 1 R G 2 y 2 Note: if we insist that R be a function graph homeomorphism 8

Graph Bisimulation Definition Two edge-labeled graphs G 1, G 2 A bisimulation is a relation R between nodes s. t. both R and R-1 are simulations 9

Set Semantics for Semistructured Data Definition Two rooted graphs G 1, G 2 are equal if there exists a bisimulation R from G 1 to G 2 such that (root(G 1), root(G 2)) R • Notation: G 1 G 2 • For trees, this is precisely our earlier definition 10

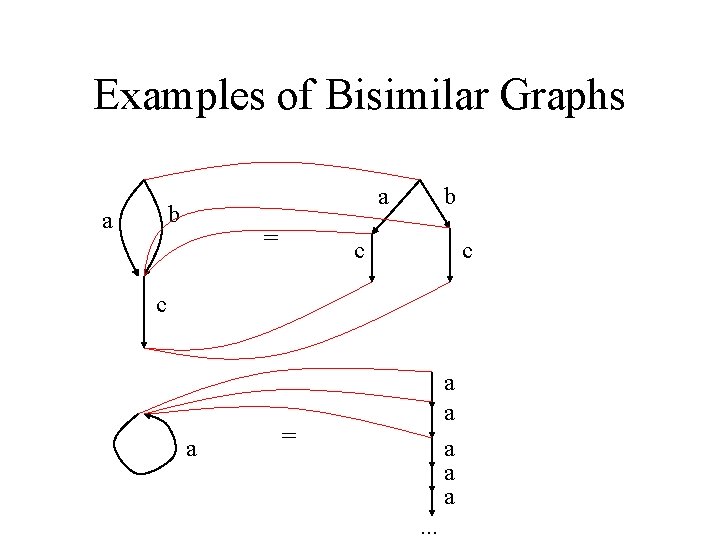
Examples of Bisimilar Graphs a b a = b c c c a a a = . . . 11

Examples of non-Bisimilar Graphs a G 1= b a a c G 2= b c • This is a simulation but not a bisimulation – Why ? • Notice: G 1, G 2 have the same sets of paths 12

Examples of Simulation • Simulation acts like “subset” {a, b} {a, b, c} a b c a b {a, b: {c}} {d, a: {e, f}, b: {c, g}} a d b e c a b f c g • Question: • if DB 1 DB 2 and DB 2 DB 1 then DB 1 DB 2 ? 13

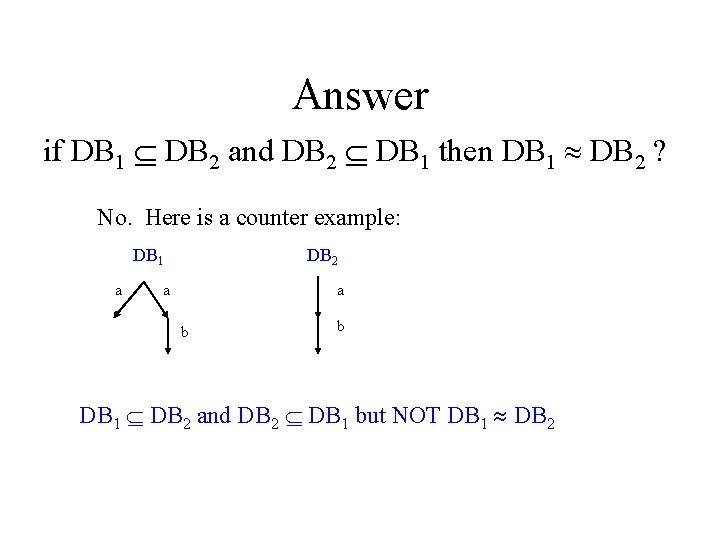
Answer if DB 1 DB 2 and DB 2 DB 1 then DB 1 DB 2 ? No. Here is a counter example: DB 1 a DB 2 a a b b DB 1 DB 2 and DB 2 DB 1 but NOT DB 1 DB 2 14

Facts About a (Bi)Simulation • The empty set is always a (bi)simulation • If R, R’ are (bi)simulations, so is R U R’ • Hence, there always exists a maximal (bi)simulation: – Checking if DB 1=DB 2: compute the maximal bisimulation R, then test (root(DB 1), root(DB 2)) in R 15

Computing a (Bi)Simulation • Computing the maximal (bi)simulation: – Start with R = nodes(G 1) x nodes(G 2) – While exists (x 1, x 2) R that violates the definition, remove (x 1, x 2) from R • This runs in polynomial time ! Better: – O((m+n)log(m+n)) for bisimulation – O(m n) for simulation – Compare to finding a graph homeomorphism ! NP Complete 16