Weaving a Tapestry Distributed Algorithms for Secure Node

Weaving a Tapestry Distributed Algorithms for Secure Node Integration, Routing and Fault Handling Ben Y. Zhao (John Kubiatowicz, Anthony Joseph) Fault-tolerant Computing Fall 2000

Why Tapestry? Distributed systems scaling to WAN n n Larger scale frequent component faults More data + centralization performance bottleneck Dynamic environment manageability complexity More principals attacks on system (e. g. Do. S) more likely Tapestry: n n Decentralized approach to location and routing focusing on fault-resilience and adaptability Builds on previous work: Plaxton trees

Background: Tapestry/Plaxton Decentralized Routing n n Local neighbor pointers Finite storage overhead Wide-area Location n Each obj maps to “root” node Store backpointers en route to root node Exploits locality Neighbor Map For “ 6271” (Octal) 0271 1271 2271 x 071 x 171 6271 xx 01 xx 11 xx 21 xxx 0 6271 xxx 2 3271 4271 5271 6271 7271 x 371 x 471 x 571 x 671 x 771 xx 31 xx 41 xx 51 xx 61 6271 xxx 3 xxx 4 xxx 5 xxx 6 xxx 7 4 3 2 1 Routing Levels

New Tapestry Mechanisms Sibling Mesh n n n Nodes in Sibling Mesh of level N share common suffix of length N Neighbors of level N+1 are siblings of level N Clusters connected w/in, possibly disconnected between regions Gateway Nodes n n Nodes that also serve as integration points Integrates new nodes w/in coverage area

Issues Routing to non-existent node Ids Node integration into Tapestry n n Populate neighbor maps, divert relevant traffic Goals: w w Low latency Limit stress on system/nodes Prevent/Limit Denial of Service attacks Approximate optimal mapping Fault-handling: n Fast detection, avoidance, and recovery

Surrogate Routing Messages to non-existent node go to “surrogate” When routing hits null entry in neighbor map … Plaxton algorithm: n n n Find global set of all nodes matching on most # of suffix bits to destination ID Use global ordering to choose 1 determinstically One hop to surrogate Tapestry distributed algorithm: n n n Find local set of routes matching on most suffix bits Deterministically (via pseudo-random hash) choose an existing alternate; route on Terminate when local node is only entry in neighbor map

Surrogate Overhead Additional hops after Plaxton version terminates Function of how even sparseness spreads through the namespace Probabilistic reasoning n n n Assumption: even ID distribution in space If perfectly evenly spaced names in namespace: overhead =< 1 Overhead = function of skew, with high probability is very small constant

Node Weaving Algorithm Phase I: n n n Given desired Guid g, nearby “gateway” Ask gateway to route to g, return hops Router for hop i+1 is sibling at level i For the i n n th hop router Copy i th neighbor map For each entry E in neighbor list, w Look at E’s higher order siblings w Traverse sibling mesh until local optima reached

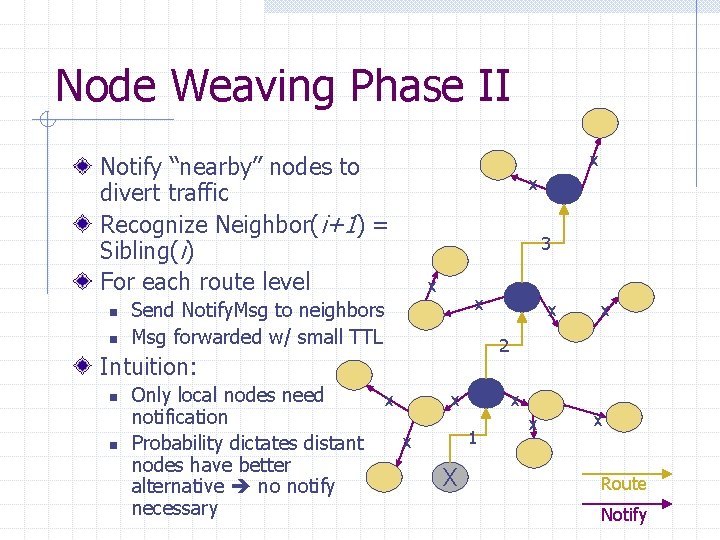
Node Weaving Phase II x Notify “nearby” nodes to divert traffic Recognize Neighbor(i+1) = Sibling(i) For each route level n n x 3 x x Send Notify. Msg to neighbors Msg forwarded w/ small TTL n Only local nodes need notification Probability dictates distant nodes have better alternative no notify necessary x 2 Intuition: n x x 1 x X x x Route Notify

Denial of Service Scenario #1 n n n Generate large # of Guids, weave each in Soln: Attach cost function to use of each Guid Key = Bit Sequence L such that w SHA-1(Guid+L+S) = [0000000]+[…] w S = random string refreshed periodically per server n n Solving inv(SHA-1) is costly Showing L with request to integrate is enough Scenario #2 n n Weave same Guid in using large # of Gateways Soln: Allow Gateways to arbitrarily limit coverage area

Fault Handling Detection: n n Routing: heartbeats to immediate neighbors Location: inventory beats to routers Resilience: n Use secondary neighbors/siblings to route around failed links/servers Repair: n n n Failed nodes marked with “invalid” flag Periodic probes (piggyback msgs) Success Change back to active status

In Progress Simulations: n n Java: Simulation of dynamic Tapestry C: Simulation of perfect topology with SGB library Algorithms: n Theoretical analysis: w Expected insertion latencies w Optimality of dynamic insertions w Optimality of overlay network distance n Routing: w Better routing using landmarks