We are Learning to Use Angle Facts Angles

We are Learning to…… Use Angle Facts

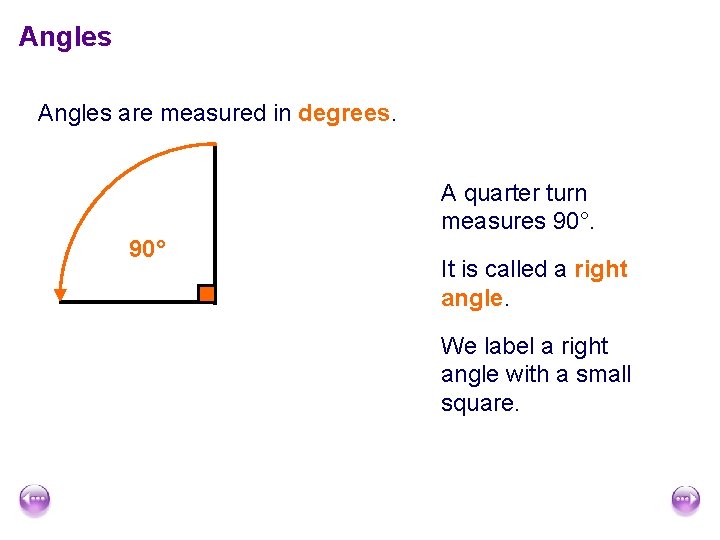
Angles are measured in degrees. A quarter turn measures 90° It is called a right angle. We label a right angle with a small square.

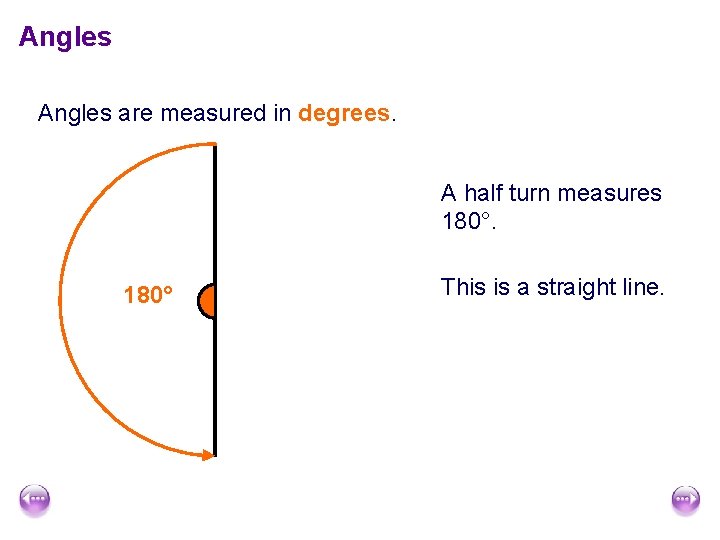
Angles are measured in degrees. A half turn measures 180° This is a straight line.

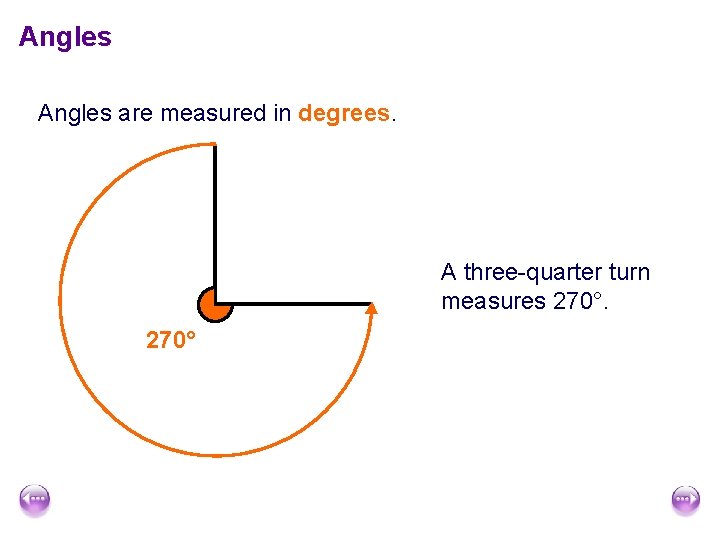
Angles are measured in degrees. A three-quarter turn measures 270°

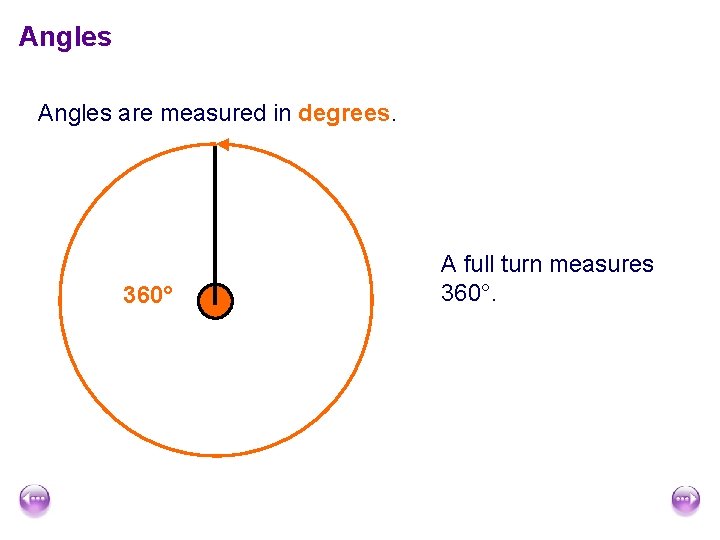
Angles are measured in degrees. 360° A full turn measures 360°.

Vertically opposite angles When two lines intersect, two pairs of vertically opposite angles are formed. a d b c a=c and b=d Vertically opposite angles are equal.

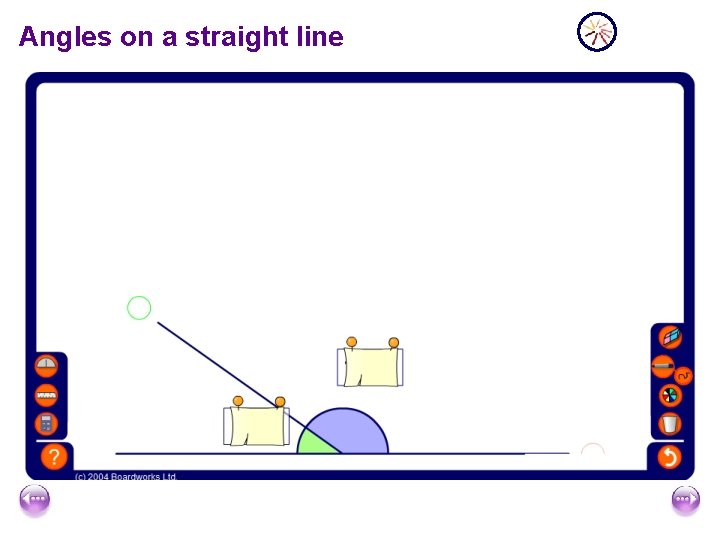
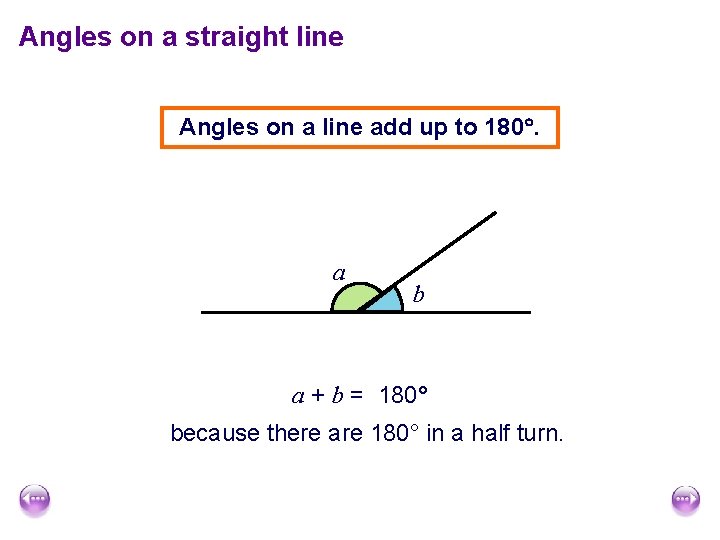
Angles on a straight line

Angles on a straight line Angles on a line add up to 180. a b a + b = 180° because there are 180° in a half turn.

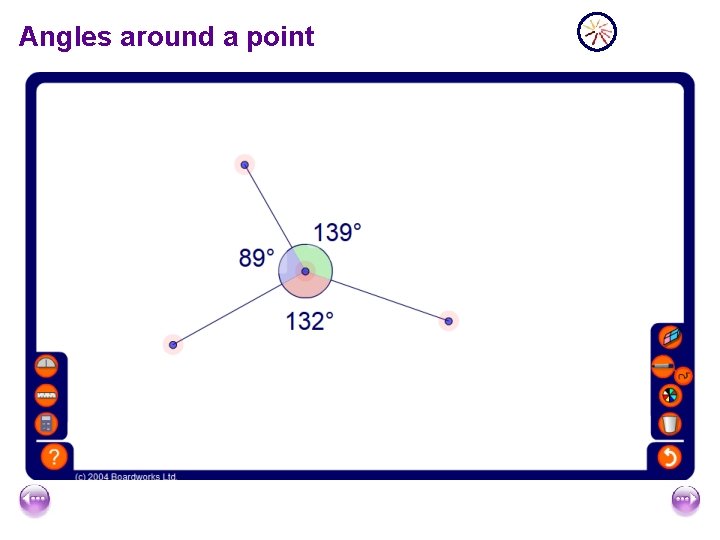
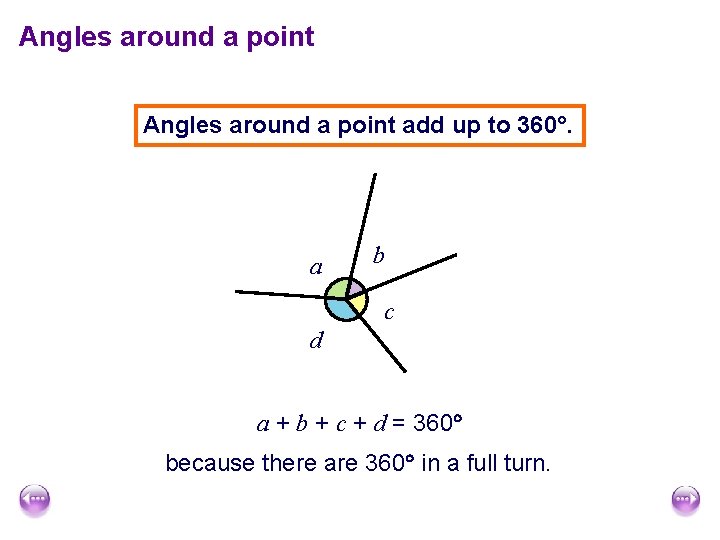
Angles around a point

Angles around a point add up to 360. a b c d a + b + c + d = 360 because there are 360 in a full turn.

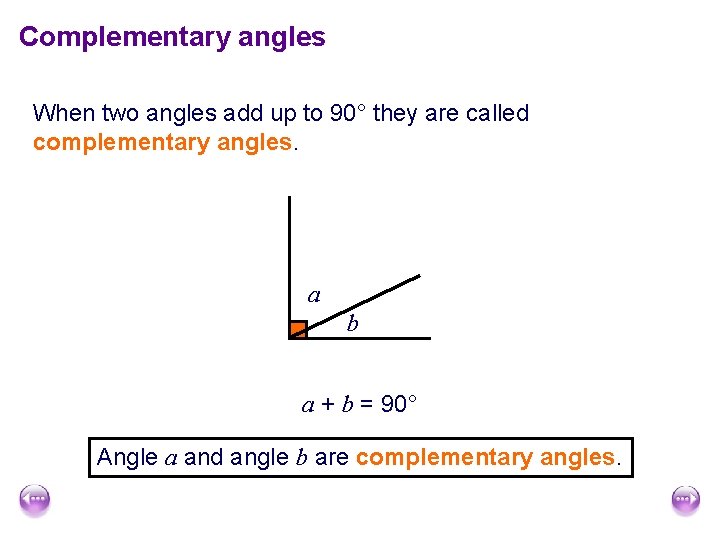
Complementary angles When two angles add up to 90° they are called complementary angles. a b a + b = 90° Angle a and angle b are complementary angles.

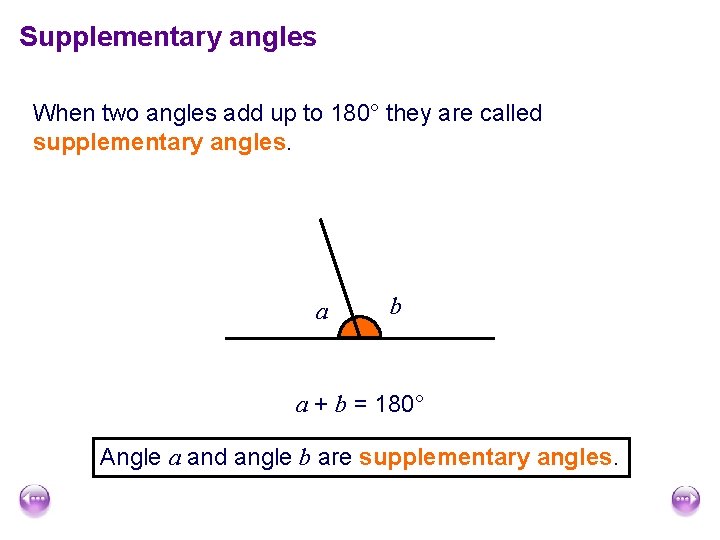
Supplementary angles When two angles add up to 180° they are called supplementary angles. a b a + b = 180° Angle a and angle b are supplementary angles.

Angle Facts • • Angles at a corner total… 90° Angles on a straight line total… 180° Angles at a point total… 360° When two straight lines cross, the opposite angles… • are equal

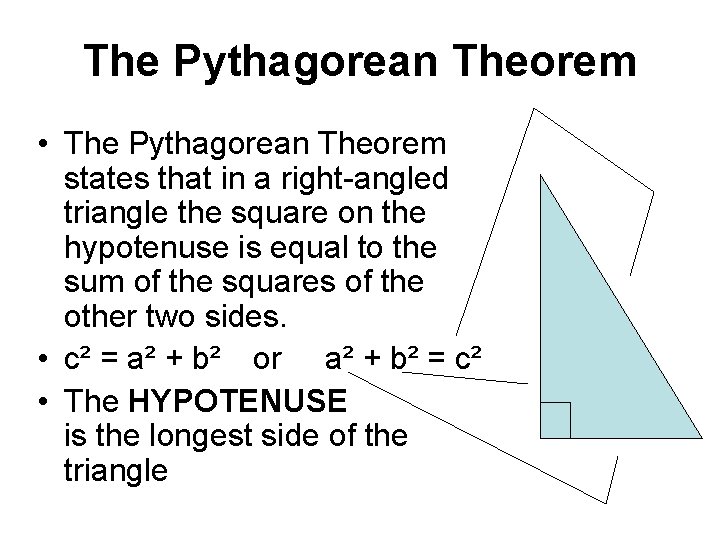
The Pythagorean Theorem • The Pythagorean Theorem states that in a right-angled triangle the square on the hypotenuse is equal to the sum of the squares of the other two sides. • c² = a² + b² or a² + b² = c² • The HYPOTENUSE is the longest side of the triangle

• Find the length of the hypotenuse of a right-angled triangle whose short sides are of length 7 cm and 18. 3 cm (one decimal place) • c² = a² + b² • c² = 7² + 18. 3² • c² = 49 + 334. 89 • c² = 383. 89 • So… • c = 383. 89 = 19. 59…. . cm • = 19. 6 cm to 1 dp

We are Learning to…… Identify the Tangent Ratio

The tangent ratio using a calculator What is the value of tan 71°? To find the value of tan 71° using a scientific calculator, start by making sure that your calculator is set to work in degrees. Key in: tan 7 1 = Your calculator should display 2. 904210878 This is 2. 90 to 3 significant figures.

We are Learning to…… Identify the Sine and Cosine Ratios

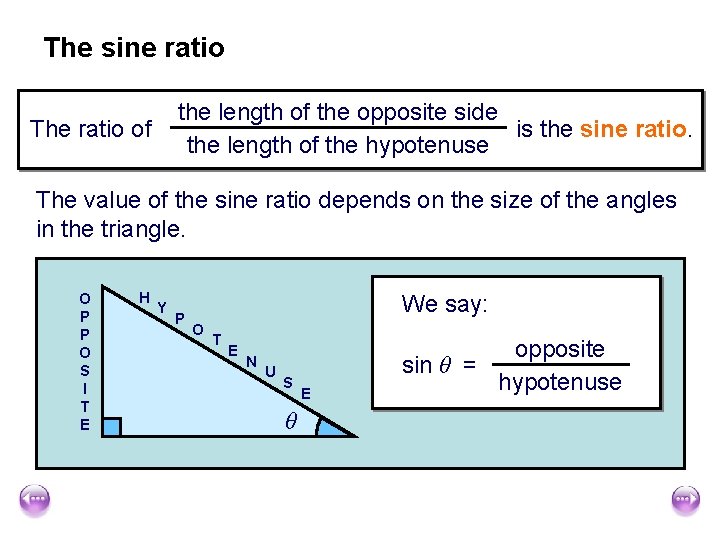
The sine ratio the length of the opposite side is the sine ratio. the length of the hypotenuse The ratio of The value of the sine ratio depends on the size of the angles in the triangle. O P P O S I T E H Y P We say: O T E N U S θ E opposite sin θ = hypotenuse

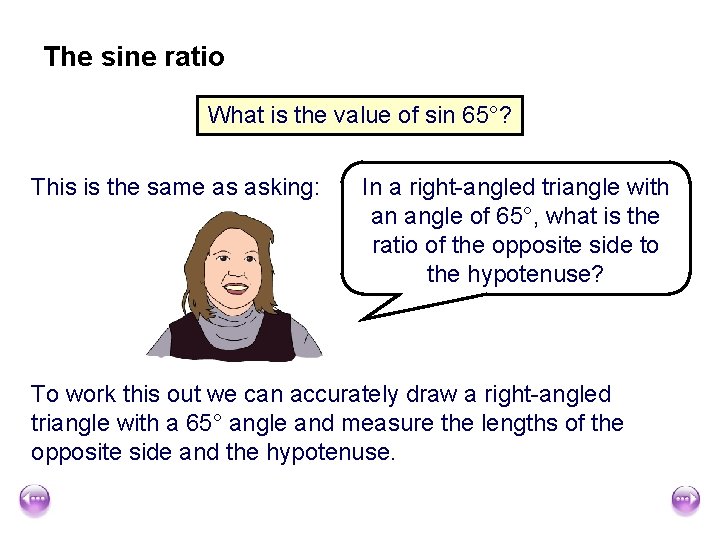
The sine ratio What is the value of sin 65°? This is the same as asking: In a right-angled triangle with an angle of 65°, what is the ratio of the opposite side to the hypotenuse? To work this out we can accurately draw a right-angled triangle with a 65° angle and measure the lengths of the opposite side and the hypotenuse.

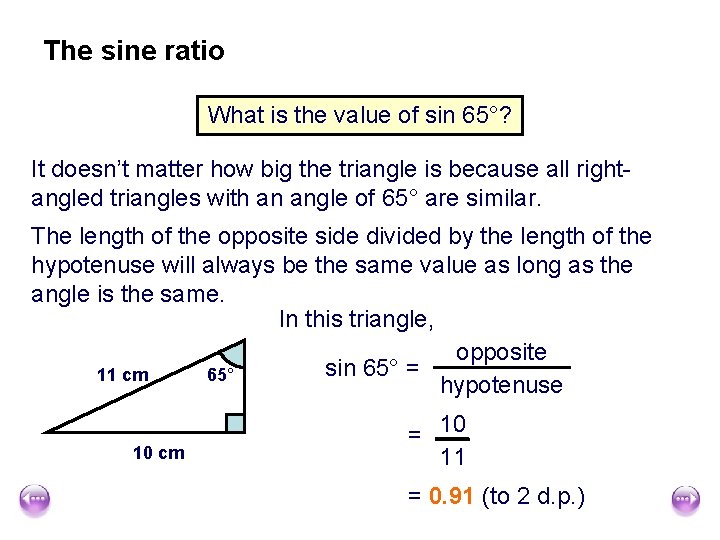
The sine ratio What is the value of sin 65°? It doesn’t matter how big the triangle is because all rightangled triangles with an angle of 65° are similar. The length of the opposite side divided by the length of the hypotenuse will always be the same value as long as the angle is the same. In this triangle, opposite sin 65° = 11 cm 65° hypotenuse 10 cm = 10 11 = 0. 91 (to 2 d. p. )

The sine ratio using a calculator What is the value of sin 65°? To find the value of sin 65° using a scientific calculator, start by making sure that your calculator is set to work in degrees. Key in: sin 6 5 = Your calculator should display 0. 906307787 This is 0. 906 to 3 significant figures.

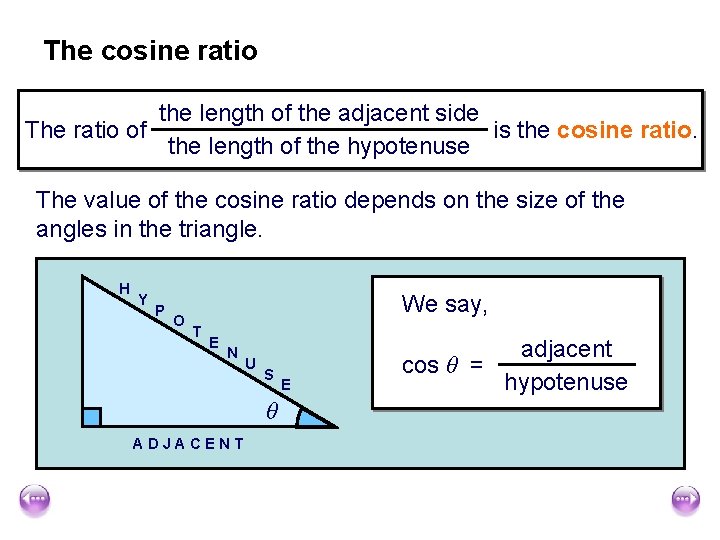
The cosine ratio the length of the adjacent side The ratio of is the cosine ratio. the length of the hypotenuse The value of the cosine ratio depends on the size of the angles in the triangle. H Y P O We say, T E N U S θ ADJACENT E adjacent cos θ = hypotenuse

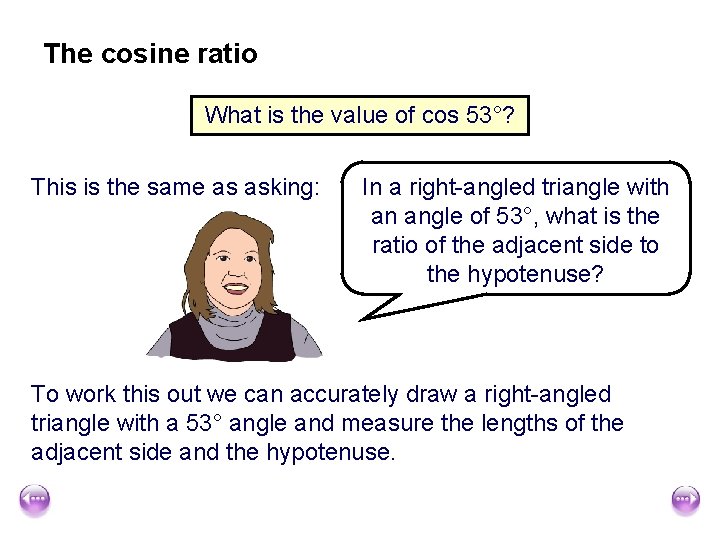
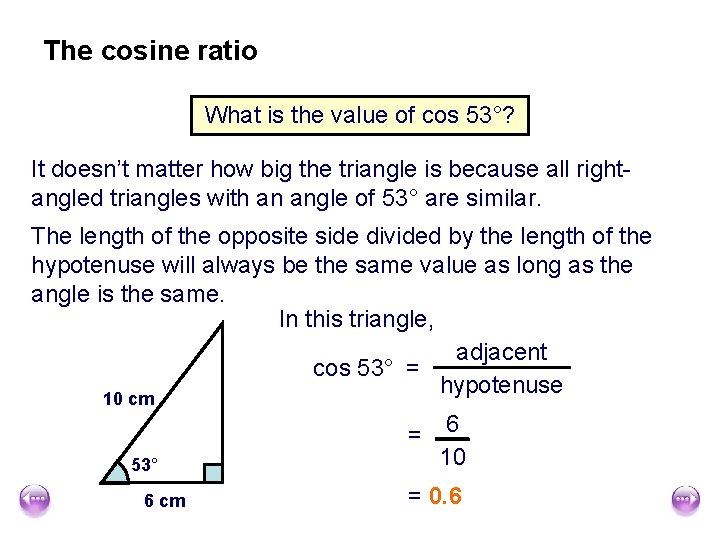
The cosine ratio What is the value of cos 53°? This is the same as asking: In a right-angled triangle with an angle of 53°, what is the ratio of the adjacent side to the hypotenuse? To work this out we can accurately draw a right-angled triangle with a 53° angle and measure the lengths of the adjacent side and the hypotenuse.

The cosine ratio What is the value of cos 53°? It doesn’t matter how big the triangle is because all rightangled triangles with an angle of 53° are similar. The length of the opposite side divided by the length of the hypotenuse will always be the same value as long as the angle is the same. In this triangle, adjacent cos 53° = hypotenuse 10 cm 53° 6 cm = 6 10 = 0. 6

The cosine ratio using a calculator What is the value of cos 25°? To find the value of cos 25° using a scientific calculator, start by making sure that your calculator is set to work in degrees. Key in: cos 2 5 = Your calculator should display 0. 906307787 This is 0. 906 to 3 significant figures.

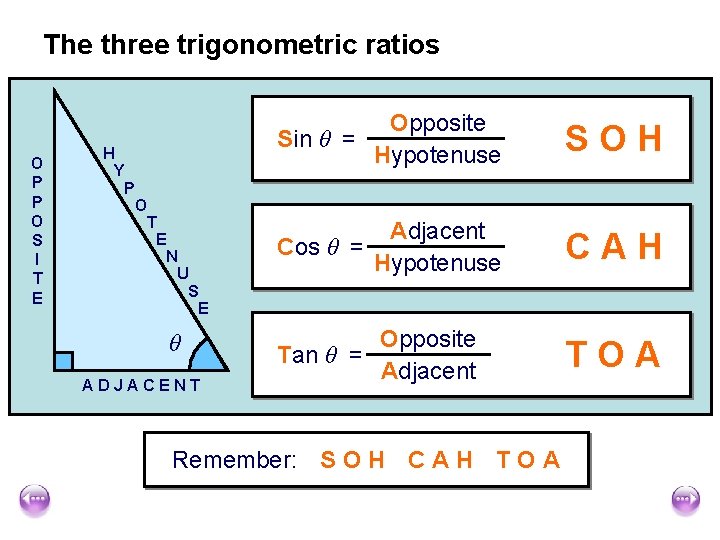
The three trigonometric ratios O P P O S I T E H Y P O T E N U S E θ ADJACENT Opposite Sin θ = Hypotenuse SOH Adjacent Cos θ = Hypotenuse CAH Opposite Tan θ = Adjacent TOA Remember: S O H C A H T O A

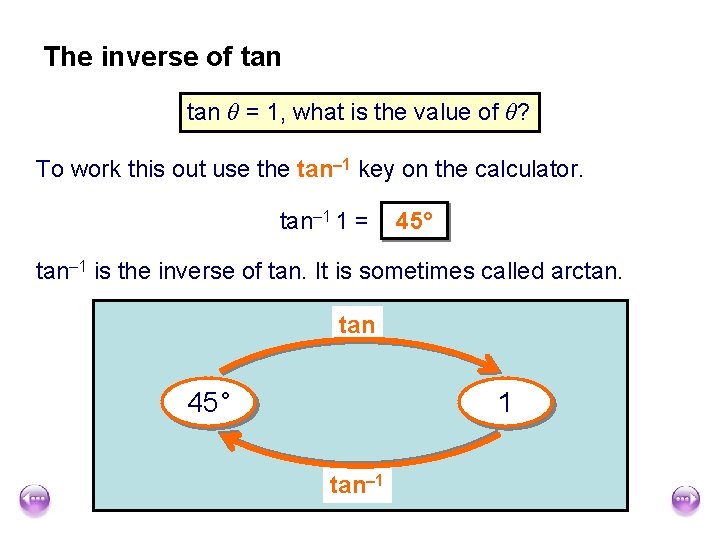
The inverse of tan θ = 1, what is the value of θ? To work this out use the tan– 1 key on the calculator. tan– 1 1 = 45° tan– 1 is the inverse of tan. It is sometimes called arctan. tan 45° 1 tan– 1

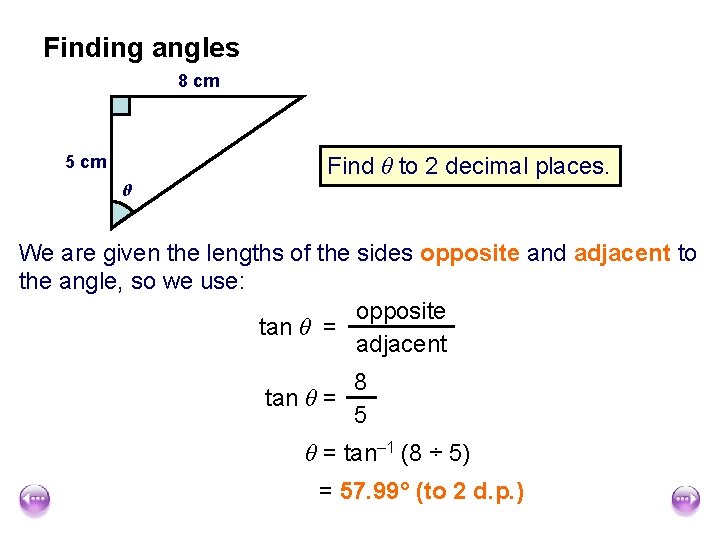
Finding angles 8 cm Find θ to 2 decimal places. 5 cm θ We are given the lengths of the sides opposite and adjacent to the angle, so we use: opposite tan θ = adjacent 8 tan θ = 5 θ = tan– 1 (8 ÷ 5) = 57. 99° (to 2 d. p. )