We are Learning to Calculate Areas of Rectangles

We are Learning to…… Calculate Areas of Rectangles, Triangles, Parallelograms and Circles

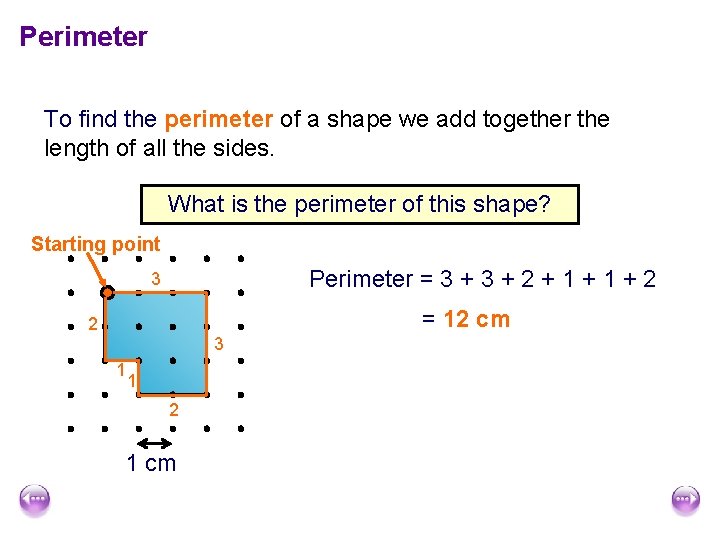
Perimeter To find the perimeter of a shape we add together the length of all the sides. What is the perimeter of this shape? Starting point Perimeter = 3 + 2 + 1 + 2 3 = 12 cm 2 3 1 1 2 1 cm

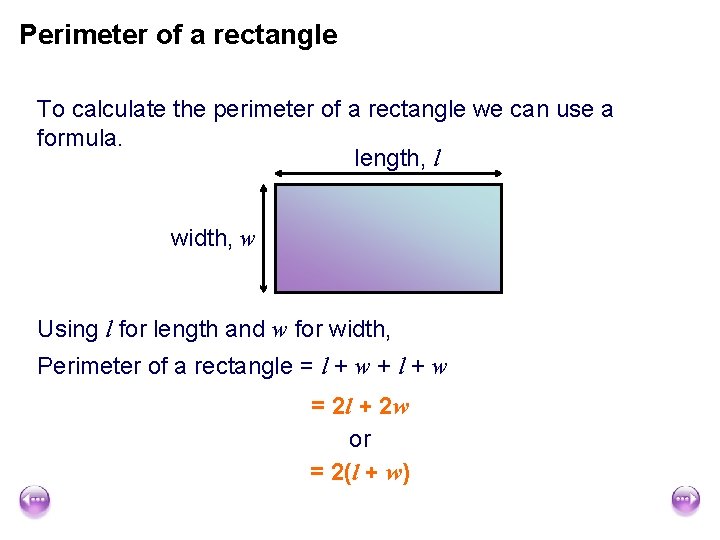
Perimeter of a rectangle To calculate the perimeter of a rectangle we can use a formula. length, l width, w Using l for length and w for width, Perimeter of a rectangle = l + w + l + w = 2 l + 2 w or = 2(l + w)

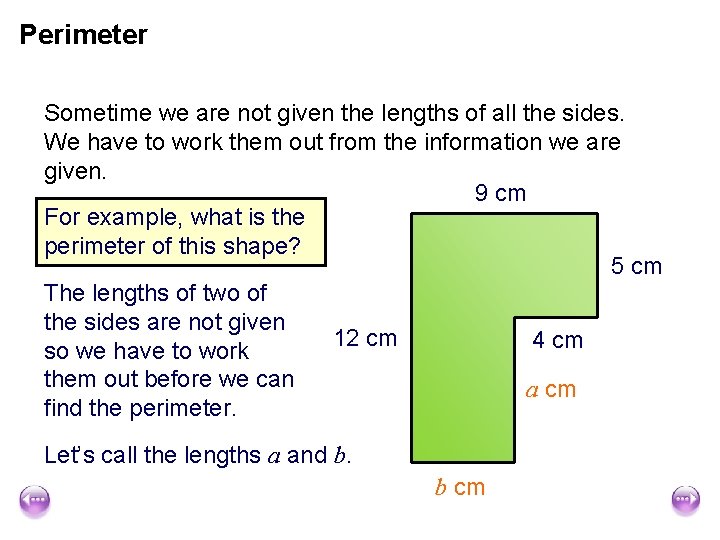
Perimeter Sometime we are not given the lengths of all the sides. We have to work them out from the information we are given. 9 cm For example, what is the perimeter of this shape? 5 cm The lengths of two of the sides are not given 12 cm 4 cm so we have to work them out before we can a cm find the perimeter. Let’s call the lengths a and b. b cm

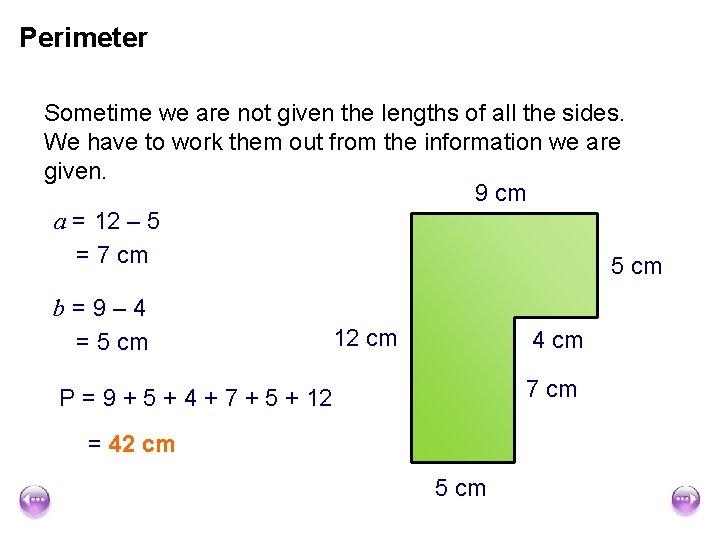
Perimeter Sometime we are not given the lengths of all the sides. We have to work them out from the information we are given. 9 cm a = 12 – 5 = 7 cm 5 cm b=9– 4 = 5 cm 12 cm 4 cm a cm 7 P = 9 + 5 + 4 + 7 + 5 + 12 = 42 cm b cm 5

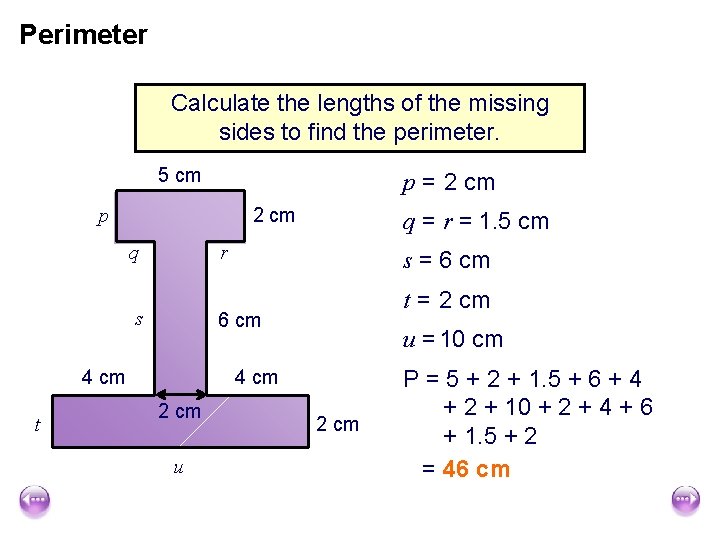
Perimeter Calculate the lengths of the missing sides to find the perimeter. 5 cm p = 2 cm p q r s s = 6 cm t = 2 cm 6 cm 4 cm t q = r = 1. 5 cm u = 10 cm 4 cm 2 cm u 2 cm P = 5 + 2 + 1. 5 + 6 + 4 + 2 + 10 + 2 + 4 + 6 + 1. 5 + 2 = 46 cm

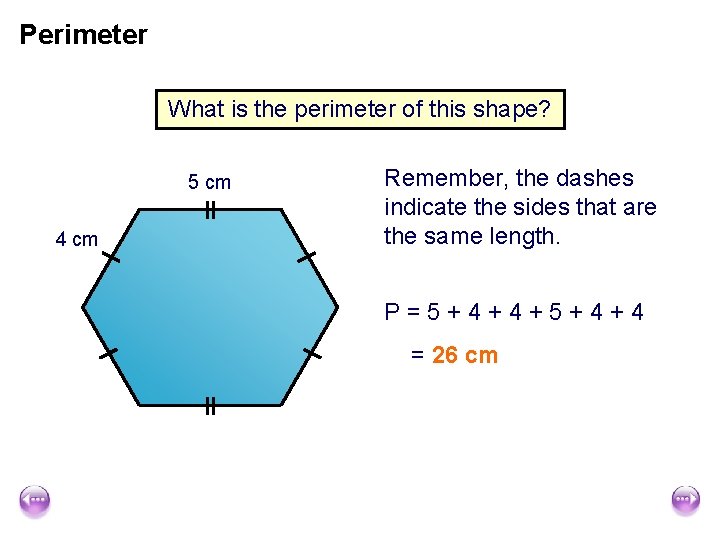
Perimeter What is the perimeter of this shape? 5 cm 4 cm Remember, the dashes indicate the sides that are the same length. P=5+4+4+5+4+4 = 26 cm

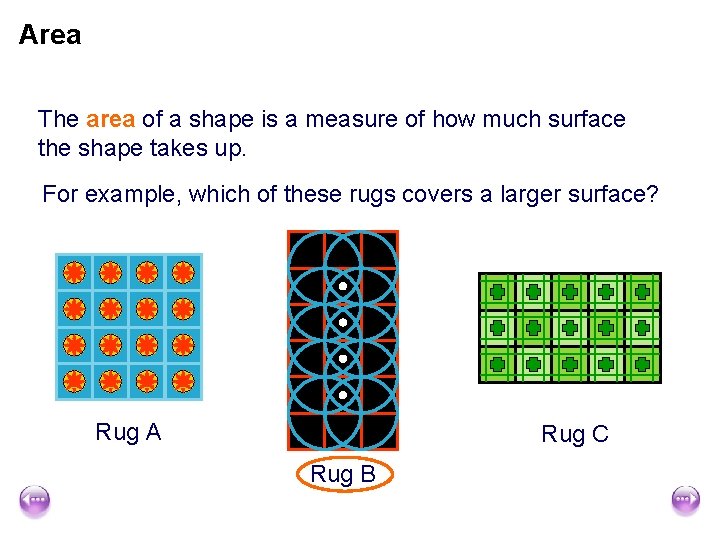
Area The area of a shape is a measure of how much surface the shape takes up. For example, which of these rugs covers a larger surface? Rug A Rug C Rug B

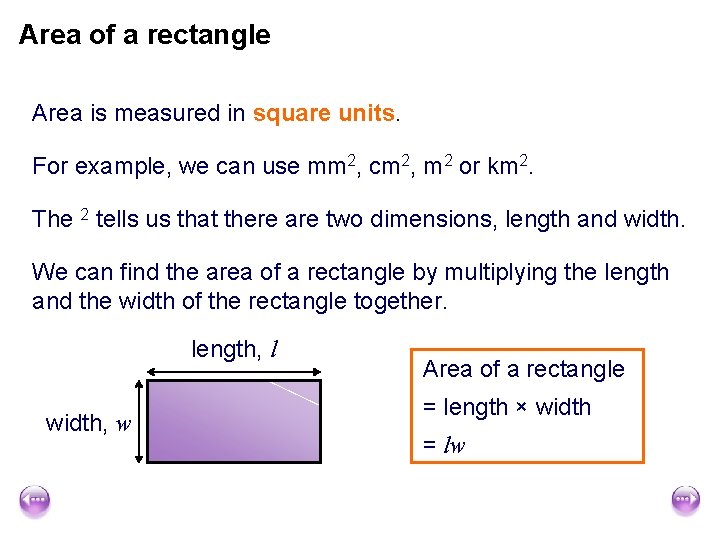
Area of a rectangle Area is measured in square units. For example, we can use mm 2, cm 2, m 2 or km 2. The 2 tells us that there are two dimensions, length and width. We can find the area of a rectangle by multiplying the length and the width of the rectangle together. length, l width, w Area of a rectangle = length × width = lw

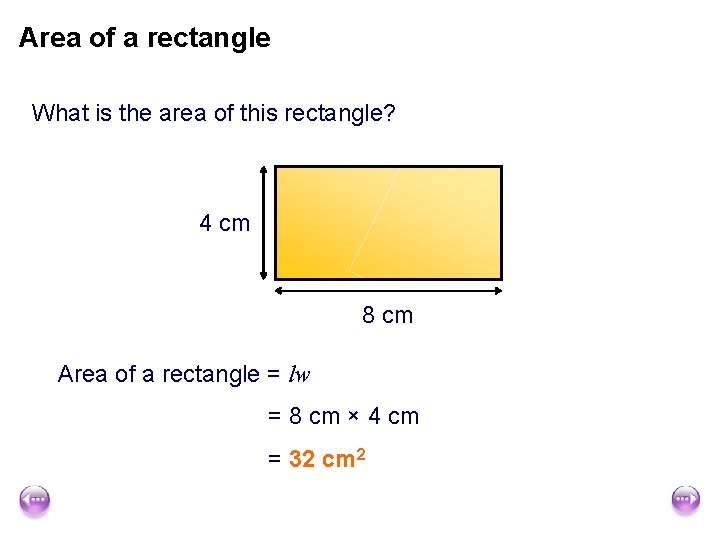
Area of a rectangle What is the area of this rectangle? 4 cm 8 cm Area of a rectangle = lw = 8 cm × 4 cm = 32 cm 2

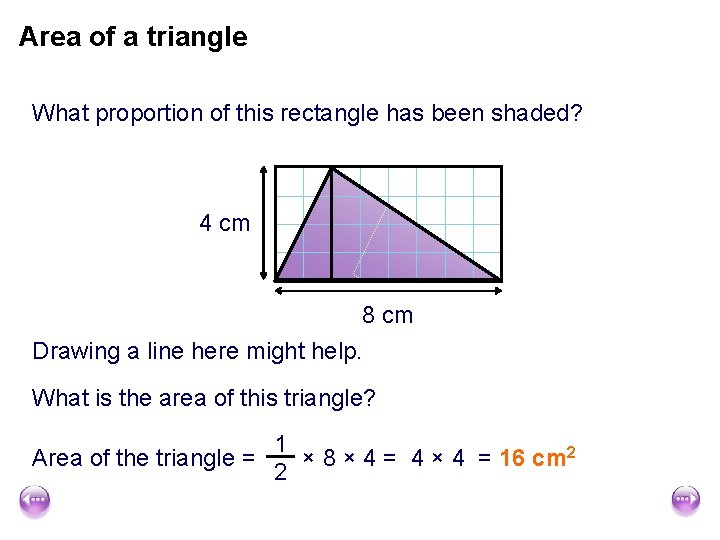
Area of a triangle What proportion of this rectangle has been shaded? 4 cm 8 cm Drawing a line here might help. What is the area of this triangle? 1 Area of the triangle = × 8 × 4 = 4 × 4 = 16 cm 2 2

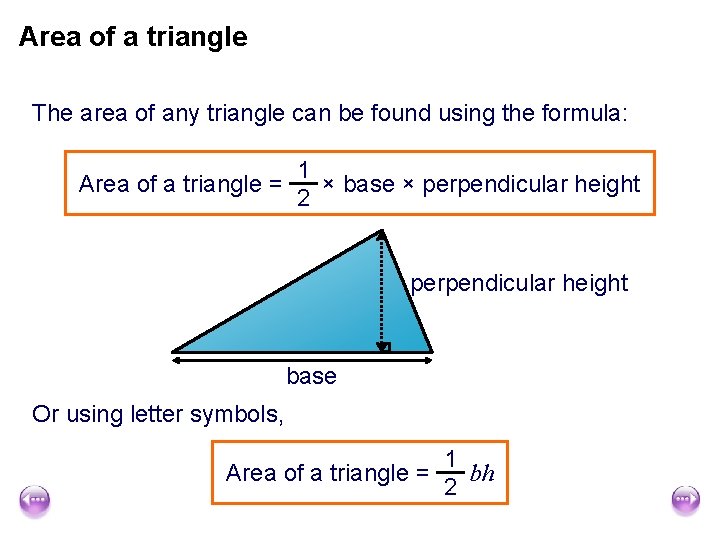
Area of a triangle The area of any triangle can be found using the formula: Area of a triangle = 1 × base × perpendicular height 2 perpendicular height base Or using letter symbols, 1 Area of a triangle = bh 2

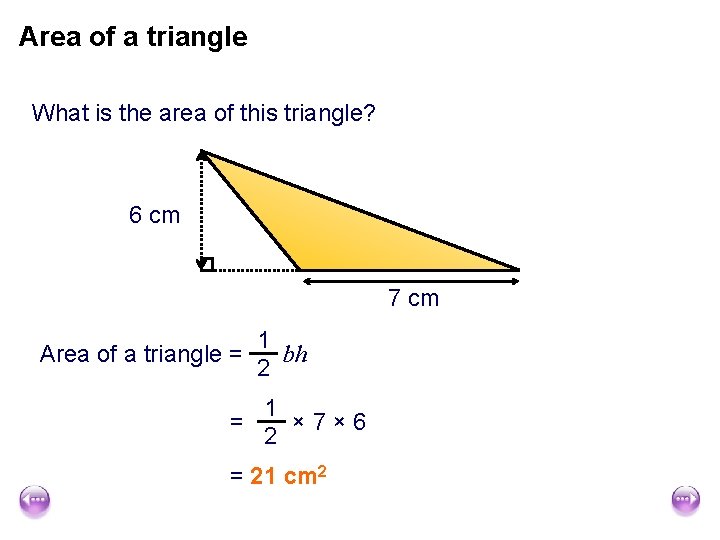
Area of a triangle What is the area of this triangle? 6 cm 7 cm 1 Area of a triangle = bh 2 1 = × 7× 6 2 = 21 cm 2

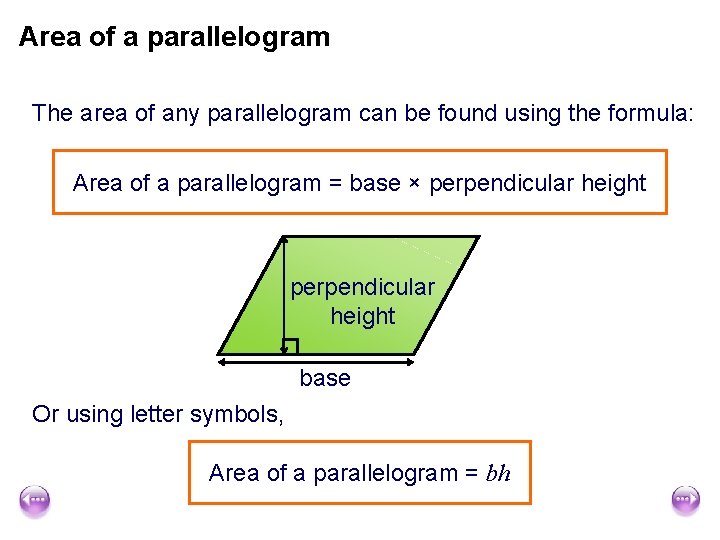
Area of a parallelogram The area of any parallelogram can be found using the formula: Area of a parallelogram = base × perpendicular height base Or using letter symbols, Area of a parallelogram = bh

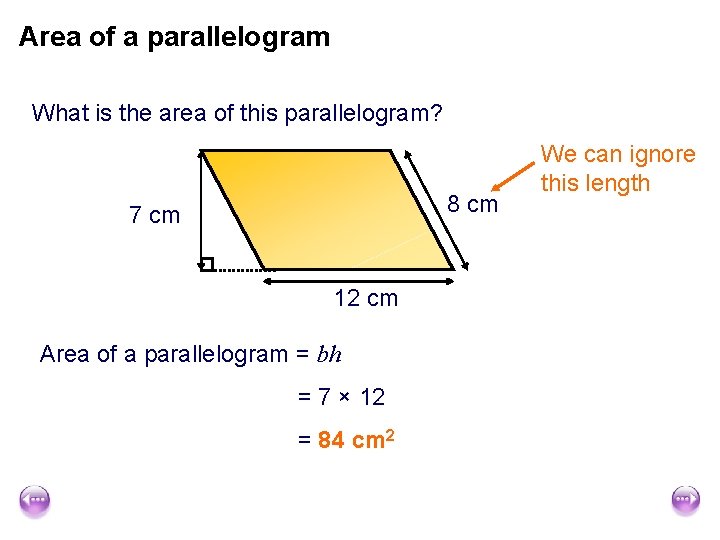
Area of a parallelogram What is the area of this parallelogram? 8 cm 7 cm 12 cm Area of a parallelogram = bh = 7 × 12 = 84 cm 2 We can ignore this length

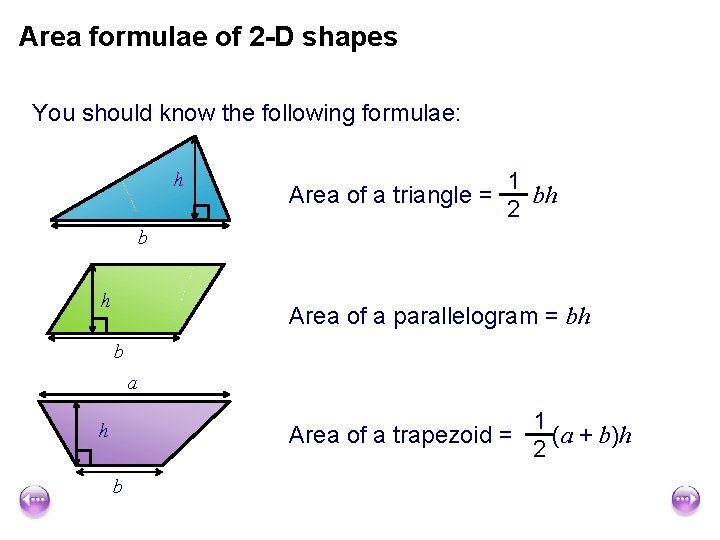
Area formulae of 2 -D shapes You should know the following formulae: h Area of a triangle = 1 bh 2 b h Area of a parallelogram = bh b a h Area of a trapezoid = b 1 (a + b)h 2

The value of π For any circle the circumference is always just over three times bigger than the radius. The exact number is called π (pi). We use the symbol π because the number cannot be written exactly. π = 3. 141592653589793238462643383279502884197169 39937510582097494459230781640628620899862803482 53421170679821480865132823066470938446095505822 31725359408128481117450284102701938521105559644 62294895493038196 (to 200 decimal places)!

Approximations for the value of π When we are doing calculations involving the value π we have to use an approximation for the value. For a rough approximation we can use 3. Better approximations are 3. 14 or 22. 7 We can also use the π button on a calculator. Most questions will tell you what approximations to use. When a calculation has lots of steps we write π as a symbol throughout and evaluate it at the end, if necessary.

The circumference of a circle For any circle, circumference π= diameter or, C π= d We can rearrange this to make an formula to find the circumference of a circle given its diameter. C = πd

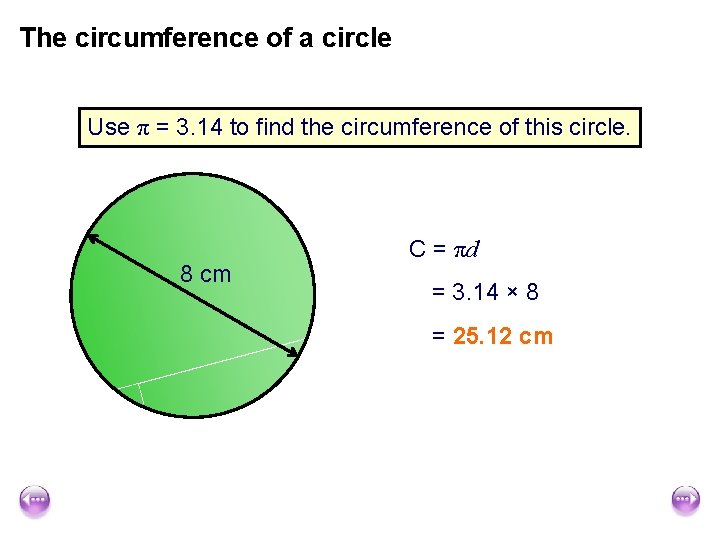
The circumference of a circle Use π = 3. 14 to find the circumference of this circle. 8 cm C = πd = 3. 14 × 8 = 25. 12 cm

Finding the circumference given the radius The diameter of a circle is two times its radius, or d = 2 r We can substitute this into the formula C = πd to give us a formula to find the circumference of a circle given its radius. C = 2πr

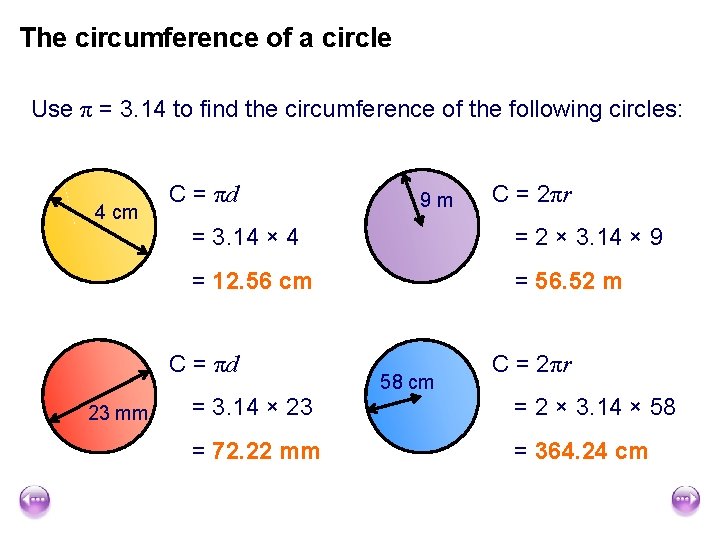
The circumference of a circle Use π = 3. 14 to find the circumference of the following circles: 4 cm C = πd C = 2πr = 3. 14 × 4 = 2 × 3. 14 × 9 = 12. 56 cm = 56. 52 m C = πd 23 mm 9 m 58 cm C = 2πr = 3. 14 × 23 = 2 × 3. 14 × 58 = 72. 22 mm = 364. 24 cm

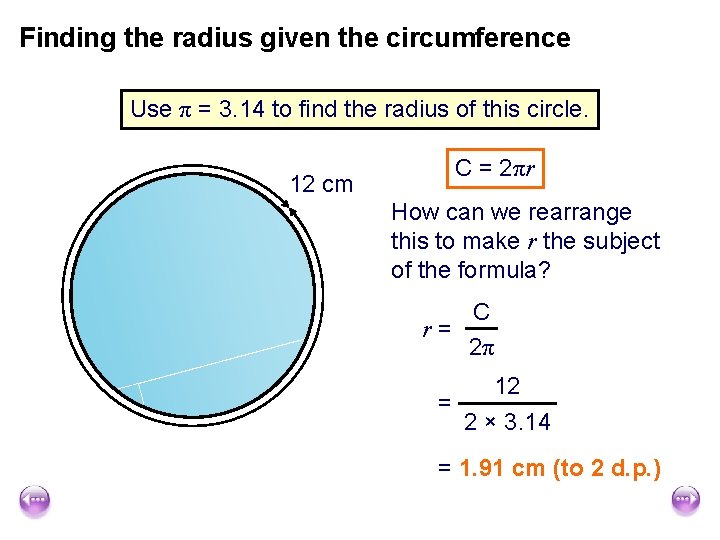
Finding the radius given the circumference Use π = 3. 14 to find the radius of this circle. 12 cm C = 2πr How can we rearrange this to make r the subject of the formula? C r= ? 2π 12 = 2 × 3. 14 = 1. 91 cm (to 2 d. p. )

Area of a circle

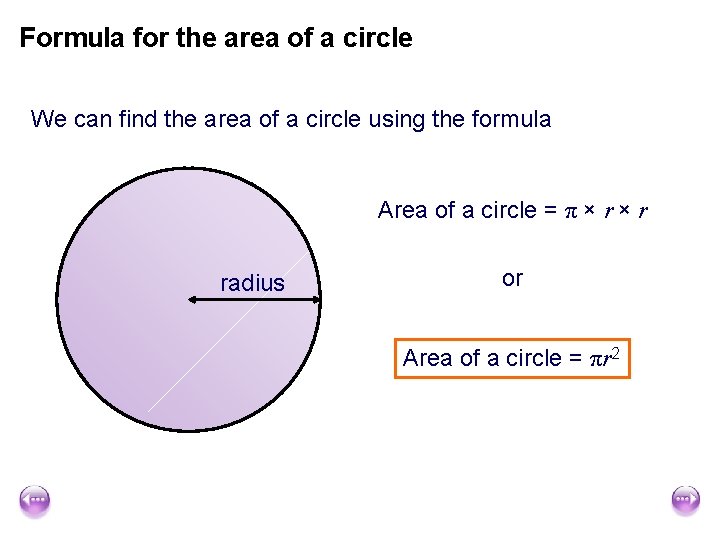
Formula for the area of a circle We can find the area of a circle using the formula Area of a circle = π × r radius or Area of a circle = πr 2

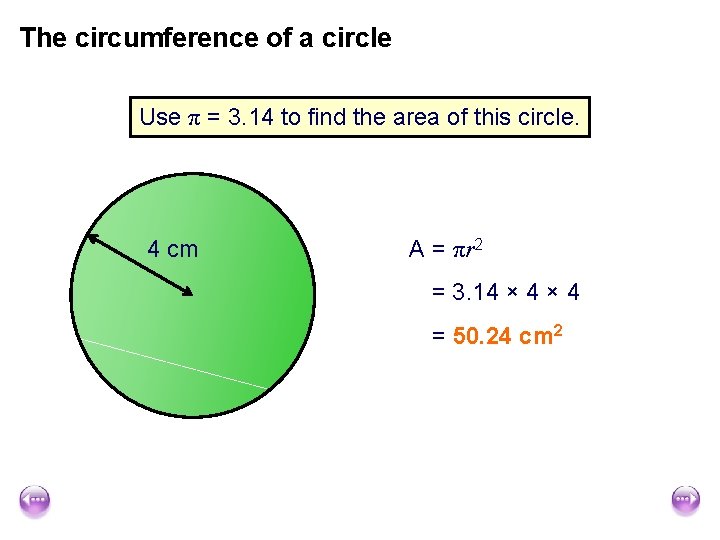
The circumference of a circle Use π = 3. 14 to find the area of this circle. 4 cm A = πr 2 = 3. 14 × 4 = 50. 24 cm 2

Finding the area given the diameter The radius of a circle is half of its radius, or d r= 2 We can substitute this into the formula A = πr 2 to give us a formula to find the area of a circle given its diameter. πd 2 A= 4

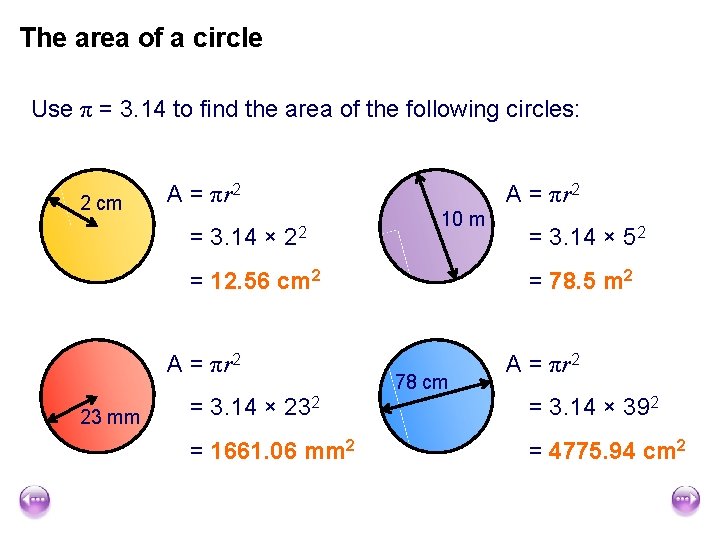
The area of a circle Use π = 3. 14 to find the area of the following circles: 2 cm A = πr 2 = 3. 14 × A = πr 2 22 10 m = 12. 56 cm 2 A = πr 2 23 mm = 3. 14 × 52 = 78. 5 m 2 78 cm A = πr 2 = 3. 14 × 232 = 3. 14 × 392 = 1661. 06 mm 2 = 4775. 94 cm 2

Circumference and Area of a Circle • The Circumference of a circle can be calculated using the formulae: • C = 2πr or C = πd • The Area of a circle can be worked out by using the formula: • A = πr² • Where d is the diameter, r is the radius and π = 3. 14 to 2 decimal places

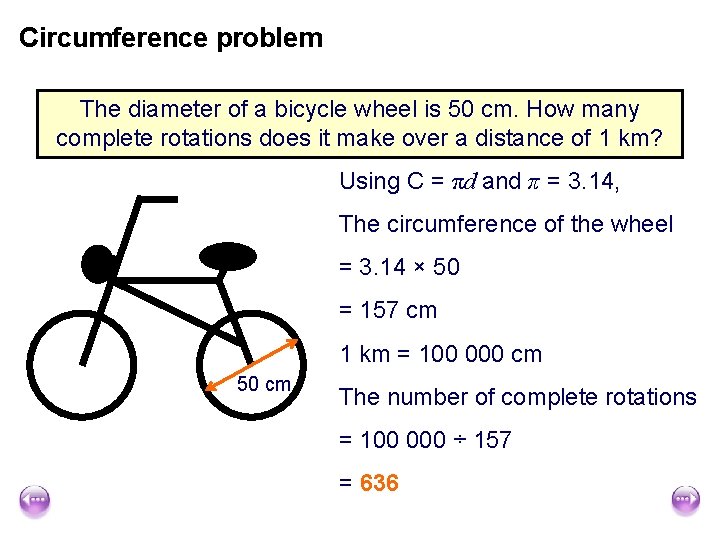
Circumference problem The diameter of a bicycle wheel is 50 cm. How many complete rotations does it make over a distance of 1 km? Using C = πd and π = 3. 14, The circumference of the wheel = 3. 14 × 50 = 157 cm 1 km = 100 000 cm 50 cm The number of complete rotations = 100 000 ÷ 157 = 636

Compound Area • If you are presented with a composite (non standard shape), don’t panic, you can still find its area easily • Look to see how you can split the shape into shapes that you do know • Try to split into rectangles, triangles, semi circles etc • Find the area of each part and add them together

• To find the perimeter of any shape just add up the lengths of each of the sides • To find the area of certain shapes, use the following formulae: • Rectangle = Length x Width • Triangle = ½ x Base x Height • Parallelogram = Base x Vertical Height • Trapezoid = ½ x Sum of the two Parallel sides x Height Mc. Graw-Hill Page 11 #s 1 – 9 HW #14 BLM 1 -4 #s 1, 4, 5, 6 a, 7

• BLM 1 -4 #s 8 – 11