WAVES Vibrations that carry energy from one place

WAVES Vibrations that carry energy from one place to another

Types of Wave n Mechanical. Examples: slinky, rope, water, sound, & earthquake n Electromagnetic. Examples: light, radar, microwaves, radio, & x-rays

What Moves in a Wave? Energy can be transported over long distances n The medium in which the wave exists has only limited movement n Example: Ocean swells from distant storms n Path of each bit of water is ellipse

Periodic Wave Source is a continuous vibration n The vibration moves outward n

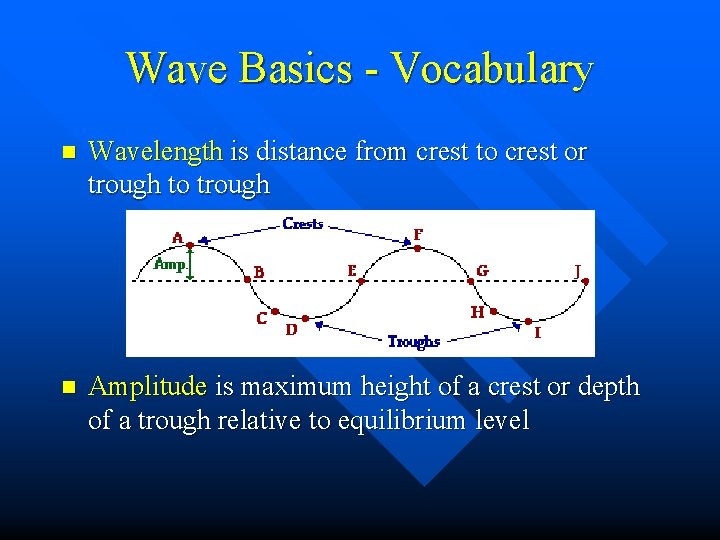
Wave Basics - Vocabulary n Wavelength is distance from crest to crest or trough to trough n Amplitude is maximum height of a crest or depth of a trough relative to equilibrium level

Frequency and Period n Frequency, f, is number of crests (waves) that pass a given point per second n Period, T, is time for one full wave cycle to pass T = 1/f f = 1/T (inverses or reciprocals) Waves /second = f seconds/wave = T n n

Unit of Frequency Hertz (Hz) n Second-1 same as 1/second or per second n Used to be “cycles per second” n

Wave Velocity n n n Wave velocity, v, is the velocity at which any part of the wave moves If wavelength = l, v = lf Example: a wave has a wavelength of 10 m and a frequency of 3 Hz (three crests pass per second. ) What is the velocity of the wave? Hint: Think of each full wave as a boxcar. What is the speed of the train?

v = lf l =v/f f = v/ l l lambda = wavelength f frequency v is sometimes called velocity of propagation (speed wave moves in medium)

Example n A ocean wave travels from Hawaii at 10 meters/sec. Its frequency is 0. 2 Hz. What is the wavelength? l = v/f = 10/0. 2 = 50 m

Second example What is the wavelength of 100 MHz FM radio waves? Use v = c = 3 x 108 m/s n l = v/f = 3 x 108 m/s ÷ 100 x 106 s-1 n = (300 x 106) ÷ (100 x 106) m n = 3. 0 m n

Another example Waves travel 75 m/s on a certain stretched rope. The distance between adjacent crests is 5. 0 m. Find the frequency and the period. n f = v/l n f = 75 m/s ÷ 5. 0 m = 15 Hz = 15 s-1 n T = 1/15 = 0. 066666 s n

Longitudinal vs. Transverse Waves n Transverse: particles of the medium move perpendicular to the motion of the wave n Longitudinal: vibrations in same direction as wave

Longitudinal Wave n Can be thought of as alternating compressions (squeezing) and expansions or rarefactions (unsqueezing)

Longitudinal Wave

Sound Wave in Air n Compressions and rarefactions of air produced by a vibrating object

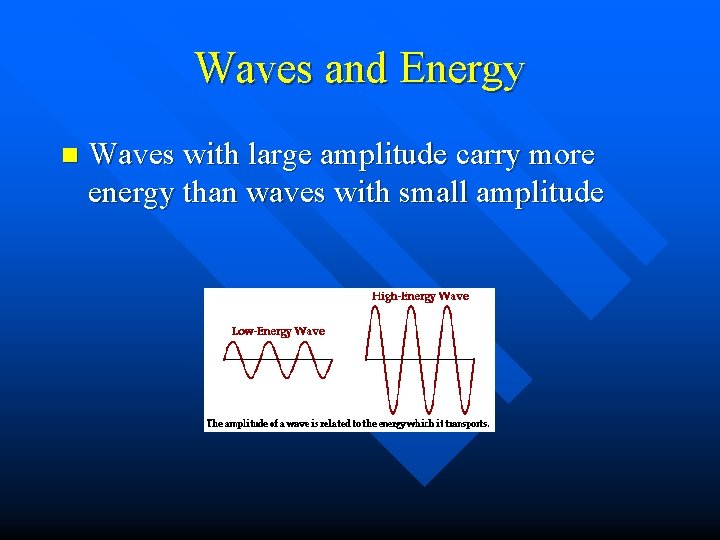
Waves and Energy n Waves with large amplitude carry more energy than waves with small amplitude

Resonance n Occurs when driving frequency is close to natural frequency (all objects have natural frequencies at which they vibrate) Tacoma Narrows bridge on the way to destruction– large amplitude oscillations in a windstorm

Interference Amplitudes of waves in the same place at the same time add algebraically (principle of superposition) n Constructive interference: n

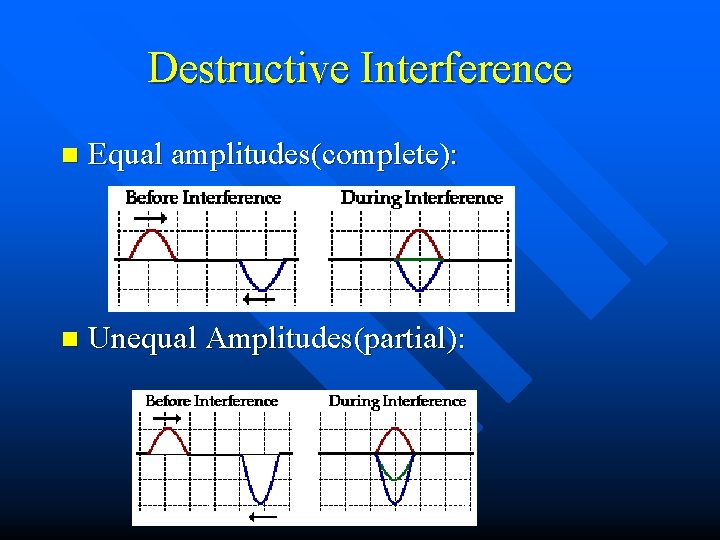
Destructive Interference n Equal amplitudes(complete): n Unequal Amplitudes(partial):

Reflection n Law of reflection: Angle of Incidence equals angle of Reflection

Hard Reflection of a Pulse n Reflected pulse is inverted

Soft Reflection of a Pulse n Reflected pulse not inverted

Soft (free-end) Reflection

Standing Waves Result from interference and reflection for the “right” frequency n Points of zero displacement - “nodes” (B) n Maximum displacement – antinodes (A) n

Formation of Standing Waves n Two waves moving in opposite directions

Examples of Standing Waves Transverse waves on a slinky n Strings of musical instrument n Organ pipes and wind instruments n Water waves due to tidal action n

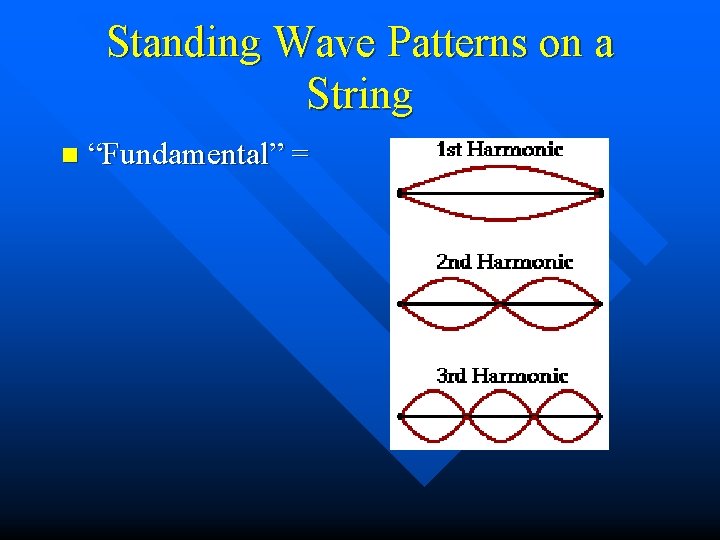
Standing Wave Patterns on a String n “Fundamental” =

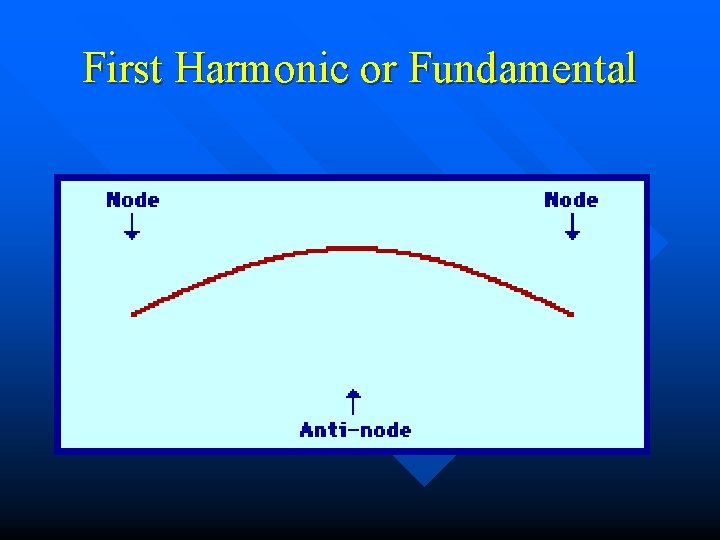
First Harmonic or Fundamental

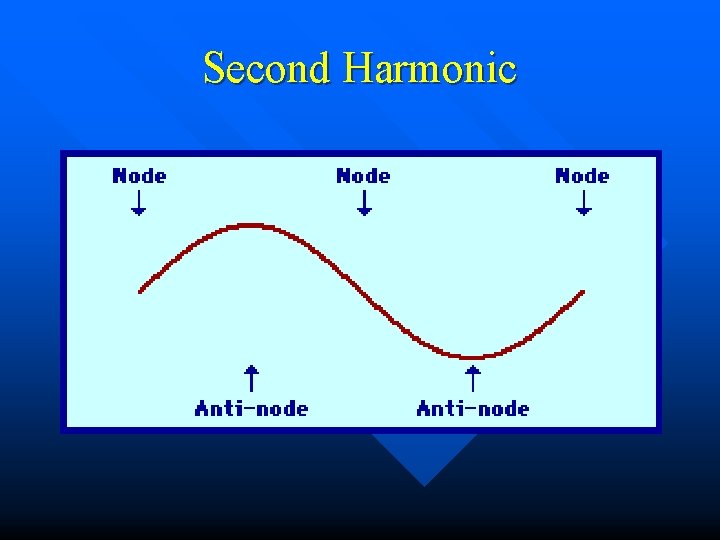
Second Harmonic

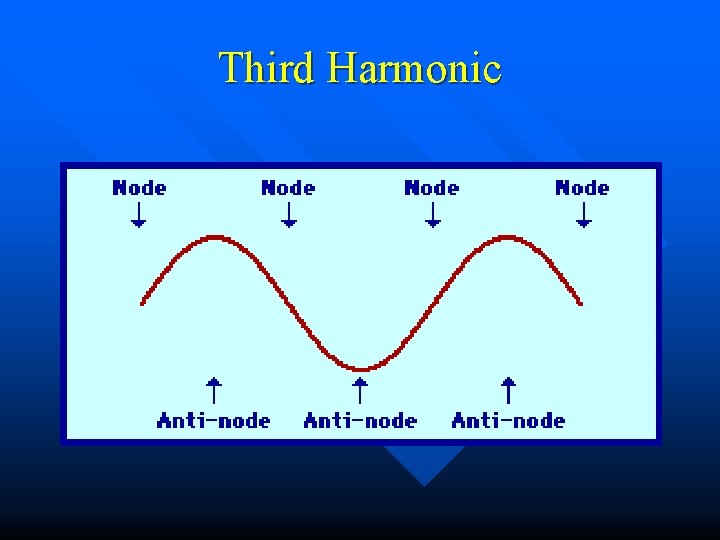
Third Harmonic

Wavelength vs. String length

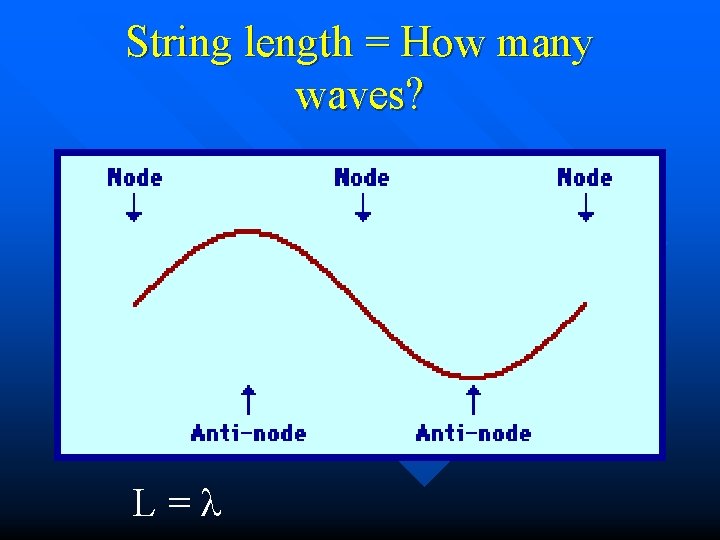
String length = How many waves? L=l

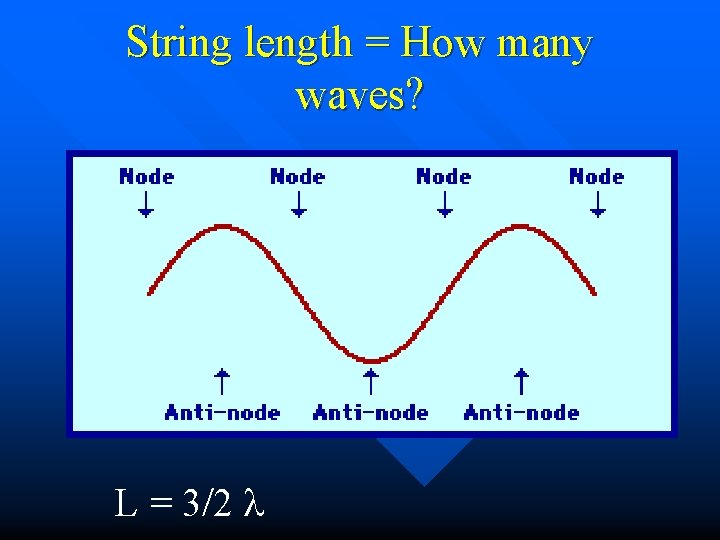
String length = How many waves? L = 3/2 l

Wavelength vs. String Length n Wavelengths of first 4 harmonics fl =v L

Frequencies are related by whole numbers Example n f 1 = 100 Hz fundamental n f 2 = 200 Hz 2 nd harmonic n f 3 = 300 Hz 3 rd harmonic n f 4 = 400 Hz 4 th harmonic n etc n Other frequencies exist but their amplitudes diminish quickly by destructive interference n

Wave velocity on a string Related only to properties of medium n Does not depend on frequency of wave n v 2 = T/m/l Tension divided by mass per unit length of string n

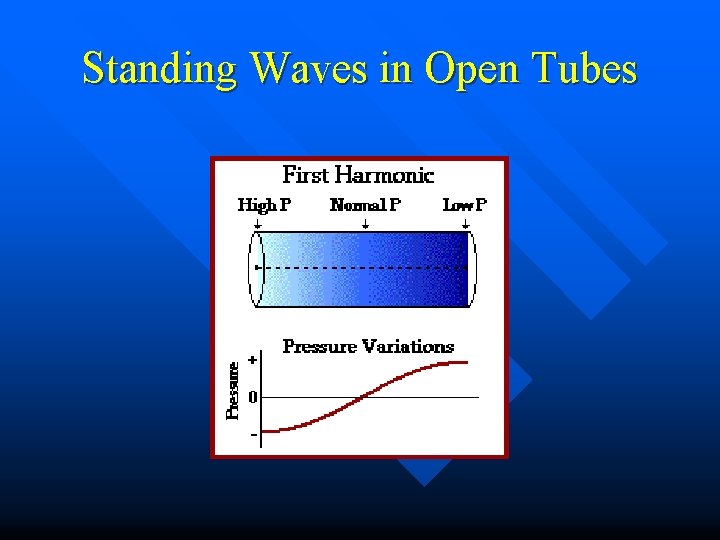
Standing Waves in Open Tubes

First Three Harmonics in Open Tube Amplitudes are largest at the open ends Amplitudes zero at the nodes

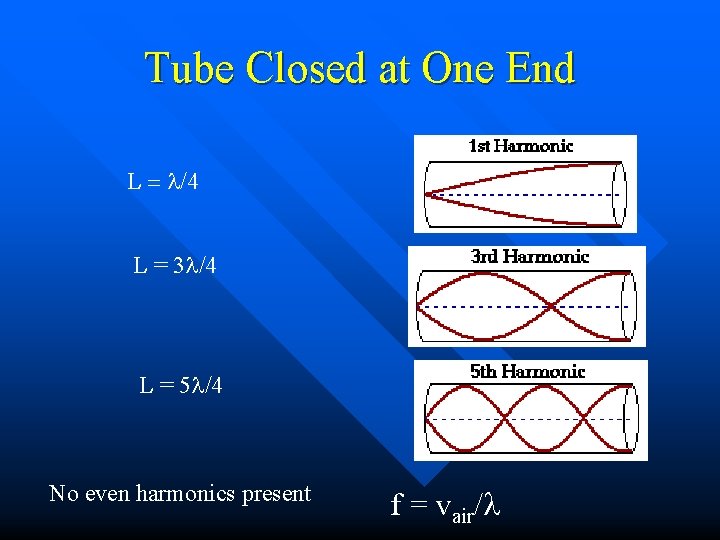
Tube Closed at One End L = l/4 L = 3 l/4 L = 5 l/4 No even harmonics present f = vair/l

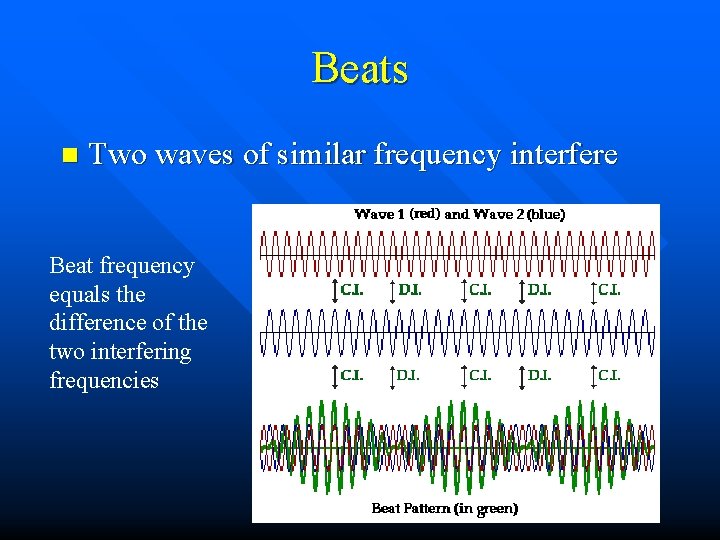
Beats n Two waves of similar frequency interfere Beat frequency equals the difference of the two interfering frequencies

Acknowledgements n Diagrams and animations courtesy of Tom Henderson, Glenbrook South High School, Illinois