Waves Part 2 resonance and more dimensions Objectives

Waves Part 2: resonance and more dimensions

Objectives • Evaluate combinations of waves from confined systems. • Explain the refraction of waves. • Explain the behavior of ocean waves near the shore.

Combinations of Waves

Standing Waves • Sum of waves of equal amplitude and wavelength traveling in opposite directions • Half-wavelength divides exactly into the available space • Wave pattern has locations of minimum and maximum variation (nodes and antinodes) • (standing longitudinal waves)

Resonance • Objects have characteristic frequencies at which standing waves are sustained • Lowest frequency = fundamental • Higher frequencies = overtones • Sustained motion is a combination of normal modes

Vibrational Modes: Clamped String Source: Griffith, The Physics of Everyday Phenomena, Figure 15. 13

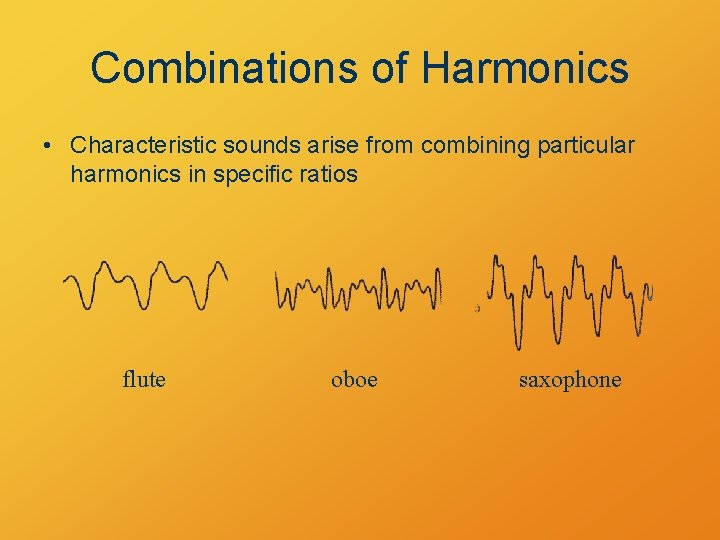
Combinations of Harmonics • Characteristic sounds arise from combining particular harmonics in specific ratios flute oboe saxophone

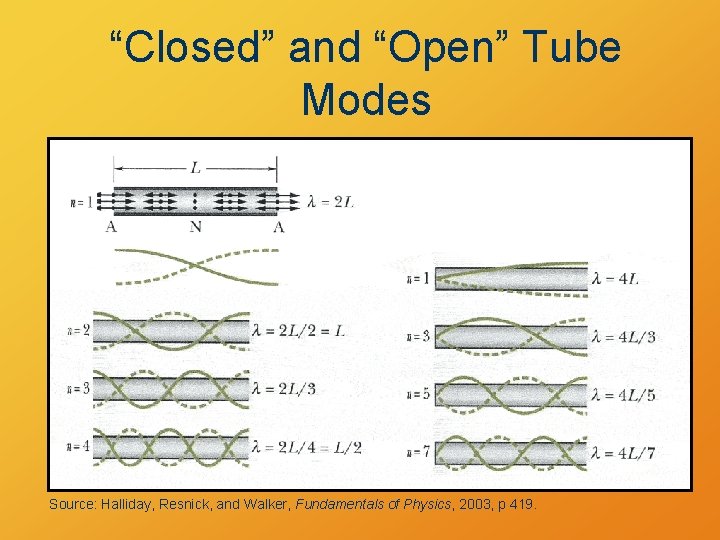
“Closed” and “Open” Tube Modes Source: Halliday, Resnick, and Walker, Fundamentals of Physics, 2003, p 419.

Poll Question Which has the lowest fundamental tone? A. B. C. D. A closed tube of length L. An open tube of length L. Both have the same fundamental tone. Not enough information.

Beats • Waves of similar frequency combine to give alternating times and places of constructive and destructive interference • Distinctive “waa-waa” sound with beat frequency equal to the difference in frequency of the component waves (Why? )

Beats • 2 -wave superposition simulation • Javascript ripple tank simulation • Sound files

Musical Tones • Octave higher = 2 the frequency • Octave + fifth: 3 the frequency • Even-tempered scale = compromise to facilitate transposition – 12 (half-) steps per octave – Half-step: 12 2 the frequency

Two-Dimensional Waves • • Ocean waves Earthquake surface waves Animation rectangular membrane Animation circular membrane

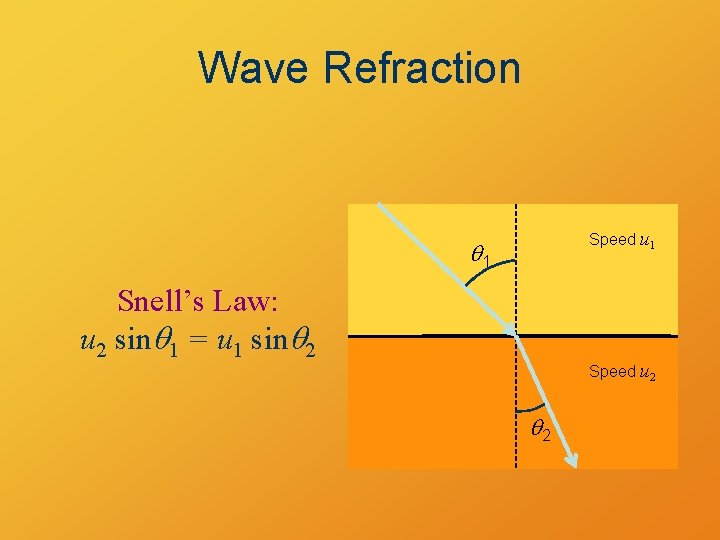
Wave Refraction Speed u 1 q 1 Snell’s Law: u 2 sinq 1 = u 1 sinq 2 Speed u 2 q 2

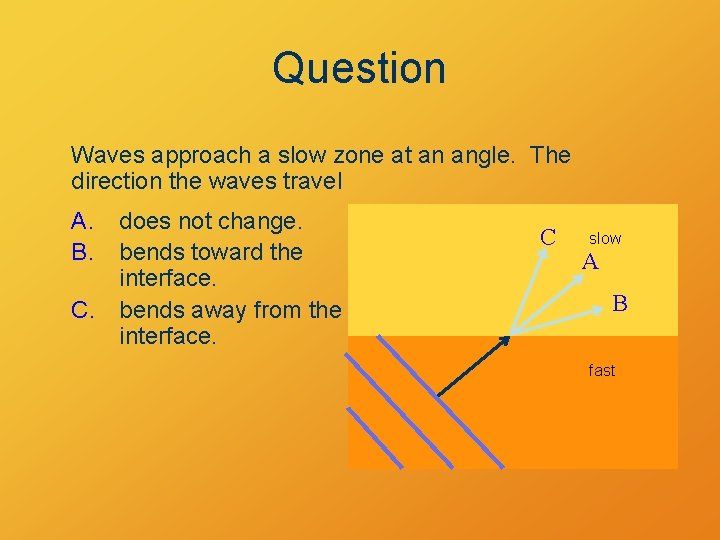
Question Waves approach a slow zone at an angle. The direction the waves travel A. B. does not change. bends toward the interface. C. bends away from the interface. C slow A B fast

Refraction Example u = 1/2 u = 3/4 u=1

Water Waves • Restoring force is gravity • Fastest in deep water, slow in shallow water • Breaking and refractive behavior in shallow water • Speed depends on wavelength • Very complicated behavior!

Question Ocean waves approaching a shore will A. bend so that the wave fronts make a greater angle with the shore. B. bend so that the wave fronts are more parallel to the shore. C. veer away from the shore. D. not change their direction.

Ocean Wave Refraction

Group Work 3. Sketch how the train of waves would move into the region of slow speed. fast slow

Breaking Wave

Shoaling and Breaking • • Waves slow in shallows by shore Wavelength shortens and amplitude rises Troughs move slower than crests Crests fall forward

Question When waves approach the shore, their increases and decreases. A. speed, mass B. force, mass C. wavelength, period D. amplitude, frequency E. amplitude, wavelength F. frequency, wavelength

Tsunami