Waves in cold fieldfree plasma General dispersionrelation for

Waves in cold field-free plasma General dispersion-relation for electrostatic and electromagnetic waves in a cold field-free plasma Assumptions i) No external fields ii) Cold plasma T=0, p=0 iii) Ions stationary. High frequency waves-> only the electrons can follow iii) Small amplitudes

General dispersion-relation for cold plasma waves • Equation of motion for electrons • Linearisation->neglect quadratic terms in the amplitude

Waves in cold plasma After linearisation the equation of motion becomes Next consider Ampere-Maxwells equation Linearisation -> Next take the time derivative and use Faradays law and the equation of motion above, then we have

Waves in cold plasma Rewriting the curl term using the BAC-CAB rule For the case of no space charge separation, this equation reduces to i. e. a wave equation, where we note the plasma frequency

Waves in cold plasma Now consider the possibility of space charge separation * To analyse this equation consider a time and space dependence as Eq* then becomes We may now have essentially two possible directions of the electric field. It may be parallel or perpendicular to the wave vector k

Waves in cold plasma First let’s consider the case when the electric field is parallel to the wave direction, then we have Case i) and therefore for an electric field different from zero we must have This means that we recover the plasma oscillations (not a wave) for which the electrons oscillate back and forth in the direction of the electric field

Dispersion-relation for plasma waves Next let’s consider the case when the electric field is perpendicular to the wave direction, let say that the electric field is in the x-direction and the wave propagates in the zdirection Case ii) For non-zero electric field we then find the dispersion-relation Transverse elctromagnetic wave in cold plasma Compare EM-waves in vacuum where

Group velocity The phase velocity of a wave is defined as From the dispersion relation we have in general The phase velocity is then So in general the phase velocity depends on the wavenumber k (or wavelength), meaning that different wavelengths propagate with different velocity. -> Dispersive waves. To find the propagation of a wave-packet, we therefore have to consider a sum(integral) of harmonic waves, a Fourier series or Fourier integral

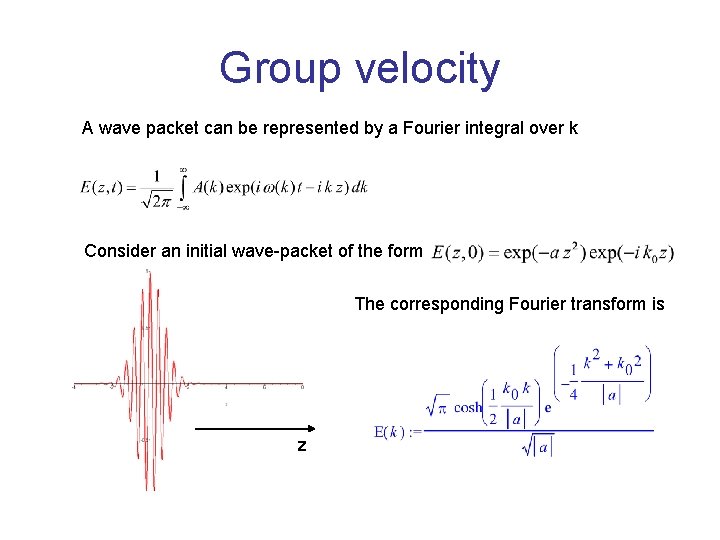
Group velocity A wave packet can be represented by a Fourier integral over k Consider an initial wave-packet of the form The corresponding Fourier transform is z

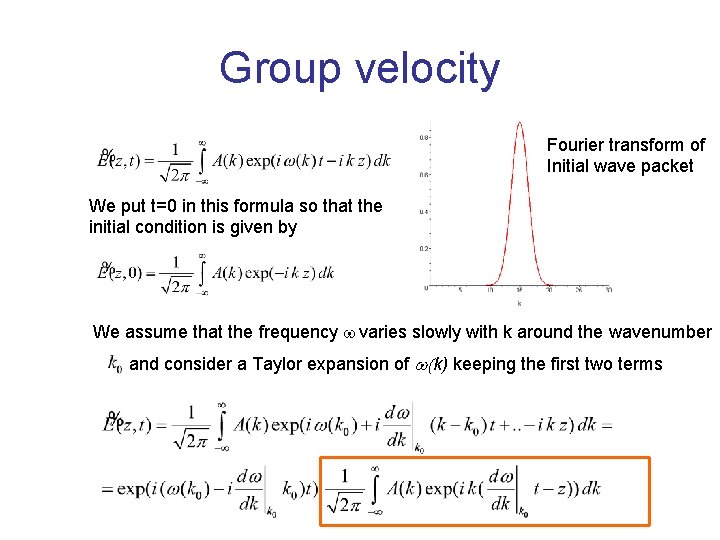
Group velocity Fourier transform of Initial wave packet We put t=0 in this formula so that the initial condition is given by We assume that the frequency w varies slowly with k around the wavenumber and consider a Taylor expansion of w(k) keeping the first two terms

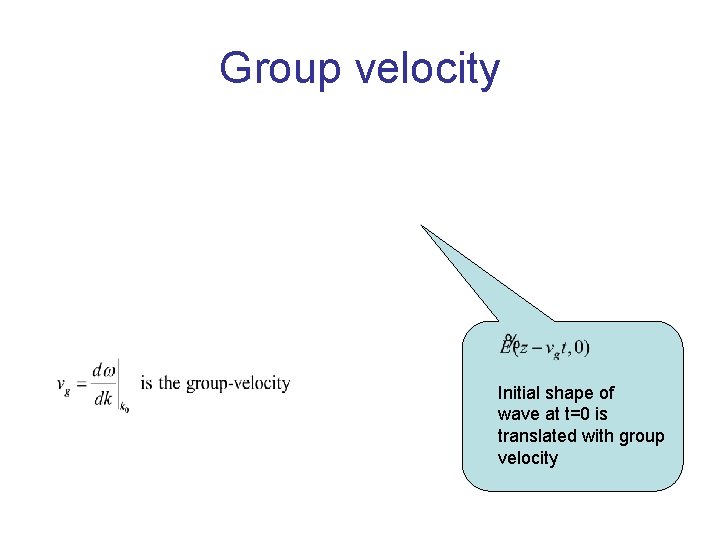
Group velocity Initial shape of wave at t=0 is translated with group velocity

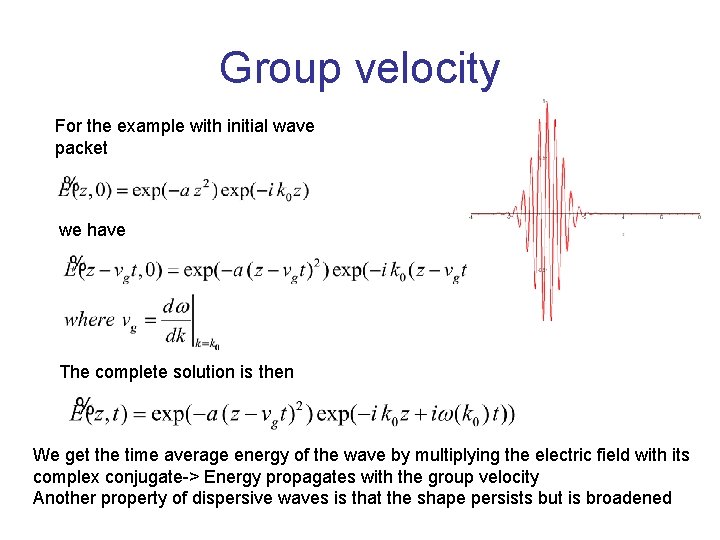
Group velocity For the example with initial wave packet we have The complete solution is then We get the time average energy of the wave by multiplying the electric field with its complex conjugate-> Energy propagates with the group velocity Another property of dispersive waves is that the shape persists but is broadened

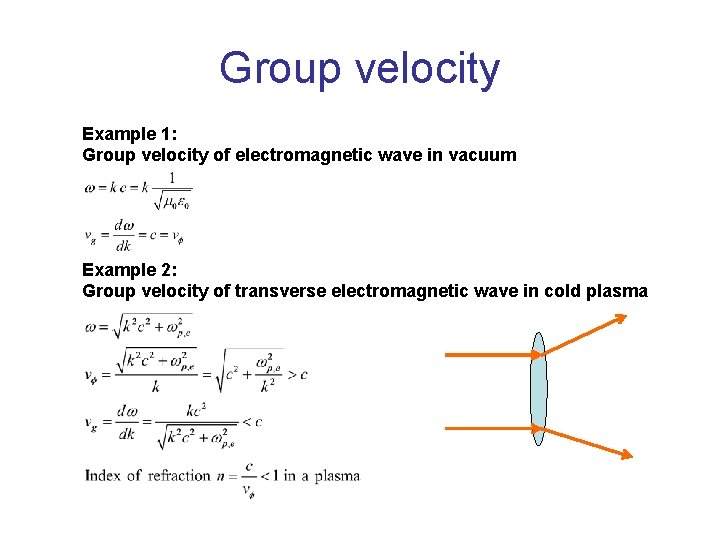
Group velocity Example 1: Group velocity of electromagnetic wave in vacuum Example 2: Group velocity of transverse electromagnetic wave in cold plasma

Dispersion-relation cold plama waves Suppose we have a wave with the form (1) From the dispersion-relation we get Together with (1) we get Now what happens if the frequency is lower than the plasma frequency

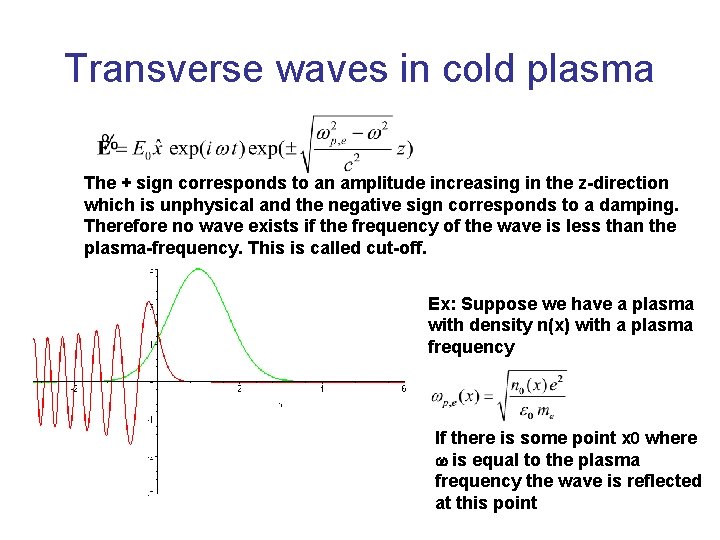
Transverse waves in cold plasma The + sign corresponds to an amplitude increasing in the z-direction which is unphysical and the negative sign corresponds to a damping. Therefore no wave exists if the frequency of the wave is less than the plasma-frequency. This is called cut-off. n 0(x) Ex: Suppose we have a plasma with density n(x) with a plasma frequency If there is some point x 0 where w is equal to the plasma frequency the wave is reflected at this point

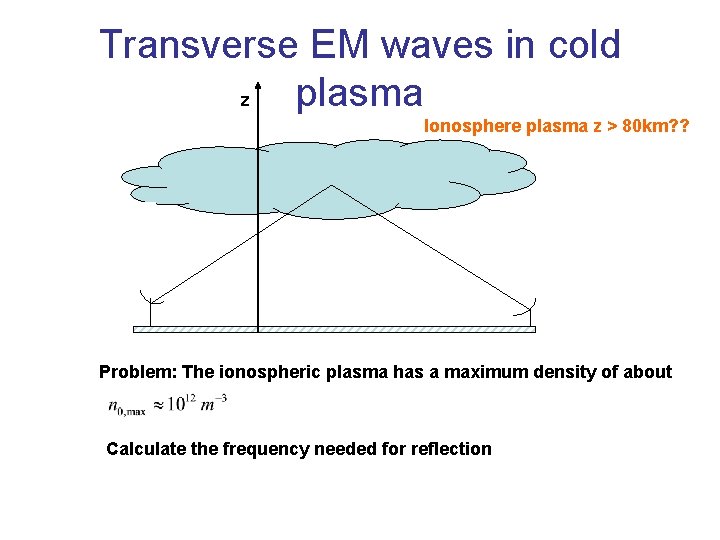
Transverse EM waves in cold plasma z Ionosphere plasma z > 80 km? ? Problem: The ionospheric plasma has a maximum density of about Calculate the frequency needed for reflection

Transverse EM waves in cold plasma Answer: The frequency must be greater than 9 MHz

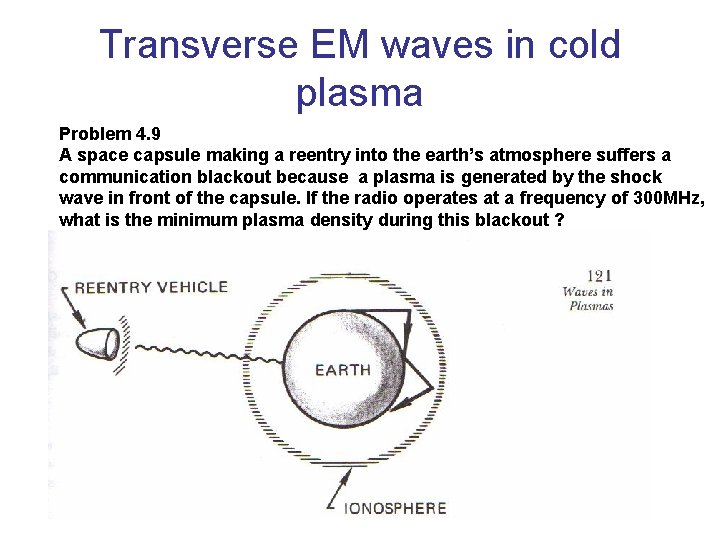
Transverse EM waves in cold plasma Problem 4. 9 A space capsule making a reentry into the earth’s atmosphere suffers a communication blackout because a plasma is generated by the shock wave in front of the capsule. If the radio operates at a frequency of 300 MHz, what is the minimum plasma density during this blackout ?

Transverse EM waves in cold plasma