Waves and Vibrations Adapted from Physics Mr Maloney

Waves and Vibrations Adapted from Physics: Mr. Maloney http: //web. mit. edu/nelsongroup/outreach/docs/waves. ppt 1

Waves are everywhere in nature ©Sound waves, ©visible light waves, ©radio waves, ©microwaves, ©water waves, ©sine waves, ©telephone cord waves, ©stadium waves, ©earthquake waves, ©waves on a string, ©slinky waves 2

What is a mechanical wave? ©a mechanical wave is a disturbance that travels through a medium from one location to another ©a mechanical wave is the motion of a disturbance ©mechanical waves differ from electromagnetic (EM) waves, because EM waves do not require a medium to travel 3

How can we model mechanical waves? ©Follow the path around the room to investigate the cause, types, and properties of mechanical waves ©Record notes, observations, and data on the front of your “journal” ©Answer the checkpoint questions on the back of your “journal” ©Stop what you are doing and answer the quick checks using your Plickers card 4

Slinky Wave ©Let’s use a slinky wave as an example ©When the slinky is stretched from end to end and is held at rest, it assumes a natural position known as the equilibrium or rest position ©To introduce a wave here we must first create a disturbance ©We must move a particle away from its rest position 5

Slinky Wave © One way to do this is to jerk the slinky forward © the beginning of the slinky moves away from its equilibrium position and then back © the disturbance continues down the slinky © this disturbance that moves down the slinky is called a pulse © if we keep “pulsing” the slinky back and forth, we could get a repeating disturbance 6

Slinky Wave © This disturbance would look something like this © This type of wave is called a LONGITUDINAL wave © The pulse is transferred through the medium of the slinky, but the slinky itself does not actually move © It is just disturbed from its rest position and then returns to it © So what really is being transferred? 7

Slinky Wave © Energy is being transferred © The metal of the slinky is the MEDIUM that transfers the energy pulse of the wave © The medium ends up in the same place as it started … it just gets disturbed and then returns to its rest position You used energy to create a disturbance on the end of the slinky. This energy was transferred the length of the slinky in the form of a wave. The particles of the medium were disturbed, but were not displaced (start and end point are the same) 8

Longitudinal Wave © Let’s take a look at this longitudinal wave. © The medium particles vibrate parallel to the motion of the pulse © Areas of the medium with high density (PRESSED together) are called compressions © Areas of the medium with low density (RARE to see FACTIONS of particles together) are called rarefactions 9

Longitudinal Wave © Sound waves are longitudinal waves © The membrane of a speaker moves to create the disturbance of air particles (the medium), and this disturbance continues to travel through the medium (air particles compress and then return to rest position) Draw It! Use dots to represent air particles and make a drawing of repeating compressions (high density) and rarefactions (low density) created by a vibrating speaker 10

Longitudinal Wave © Still have questions? Watch the video to learn more about longitudinal waves © Checkpoint Questions ©Explain how waves transfer energy without transferring matter. ©Explain the relationship between the direction of the disturbance, medium movement, wave movement, and energy transfer in a longitudinal wave. ©Compare and contrast compressions and rarefactions. ©Why can’t sound waves travel in outer space? 11

Transverse waves ©A second type of wave is a transverse wave ©We said in a longitudinal wave the pulse travels in a direction parallel to the disturbance ©In a transverse wave the pulse travels perpendicular to the disturbance 12

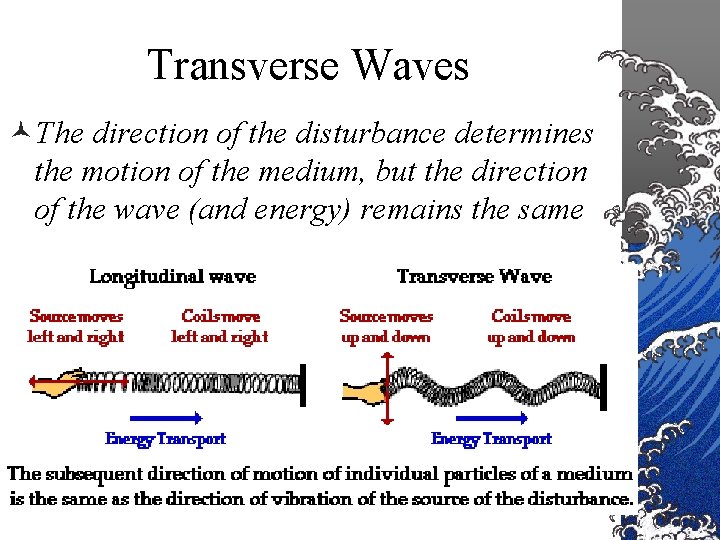
Transverse Waves ©The direction of the disturbance determines the motion of the medium, but the direction of the wave (and energy) remains the same 13

Transverse Waves ©You can produce transverse waves with the slinky (try it!) ©To break the disturbance down into parts, we are going to use the bead string ©We will be drawing the locations of the beads on your paper with different color highlights representing different phases of the disturbance ©Be sure to try the movements a few times to observe position and direction of each bead before drawing it 14

Transverse Waves ©Equilibrium or Rest Position – lay the bead string out along the “x-axis” of your paper and mark the position of the beads by placing a dash under each bead ©Crest – move the end of your string up the “y-axis” and stop at the “top” ©Mark the locations of your beads with a different color highlighter ©Trough – move the end of your string down the “y-axis” and stop at the “bottom” (go as far below the equilibrium as you went above) 15

Transverse Waves ©Mark the locations of your beads with a different color highlighter ©Add arrows to show if the beads moved up or down (use the previous position marks as a reference) ©Return to Rest Positon (Equilibrium ©Mark the locations of your beads with a different color highlighter ©Add arrows to show if the beads moved up or down (use the previous position marks 16 as a reference)

Transverse Waves ©The motion of the disturbance was perpendicular (transverse) ©One wave was created from the cycle of up to crest, down to trough, back to equilibrium ©One cycle produces one pulse ©If you keep doing it periodically over and over again, the motion creates periodic waves ©Periodic motion creates waves (pulses) that repeat at regular time intervals (periods) 17

Transverse Waves © Checkpoint Questions ©Explain how waves transfer energy without transferring matter. ©Explain the relationship between the direction of the disturbance, medium movement, wave movement, and energy transfer in a transverse wave. ©How can the different types of waves be described in terms of movement and energy? 18

Anatomy of a Wave ©Now we can begin to describe the anatomy of our waves ©We will use a transverse wave to describe this since it is easier to see the pieces 19

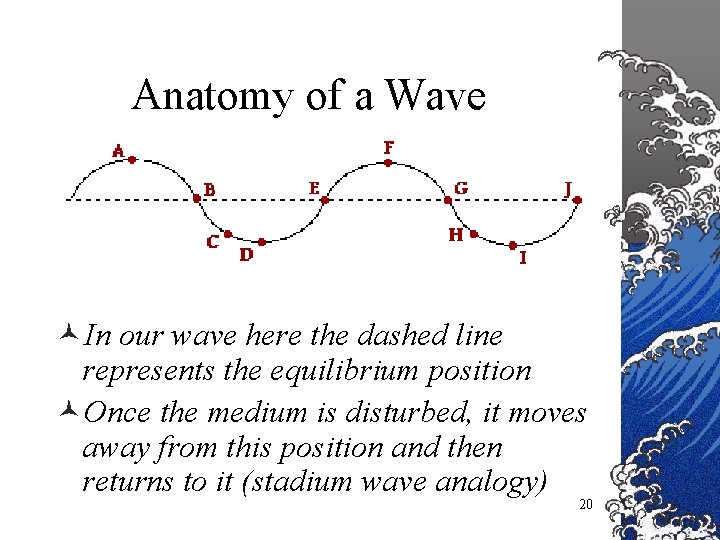
Anatomy of a Wave ©In our wave here the dashed line represents the equilibrium position ©Once the medium is disturbed, it moves away from this position and then returns to it (stadium wave analogy) 20

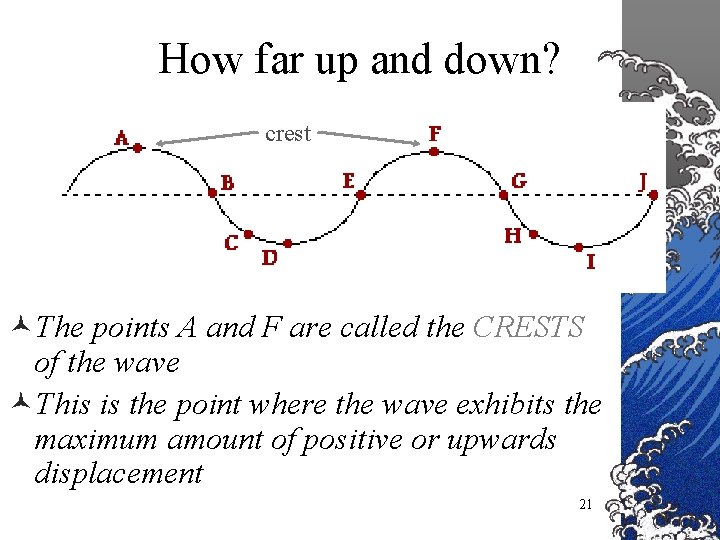
How far up and down? crest ©The points A and F are called the CRESTS of the wave ©This is the point where the wave exhibits the maximum amount of positive or upwards displacement 21

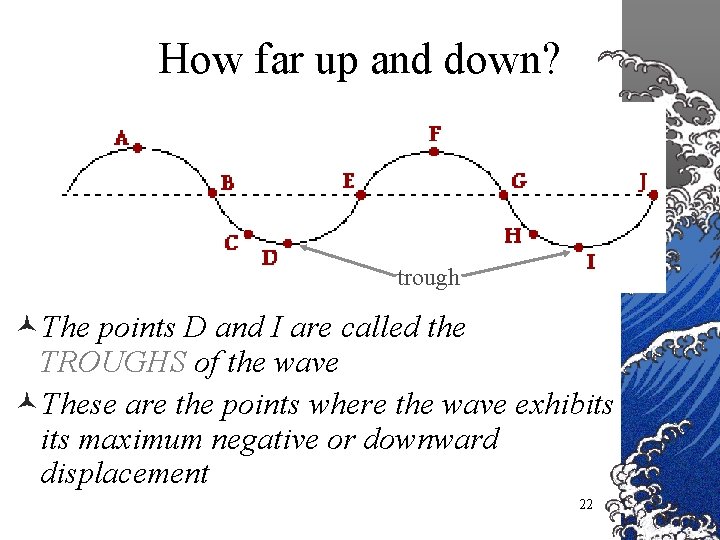
How far up and down? trough ©The points D and I are called the TROUGHS of the wave ©These are the points where the wave exhibits maximum negative or downward displacement 22

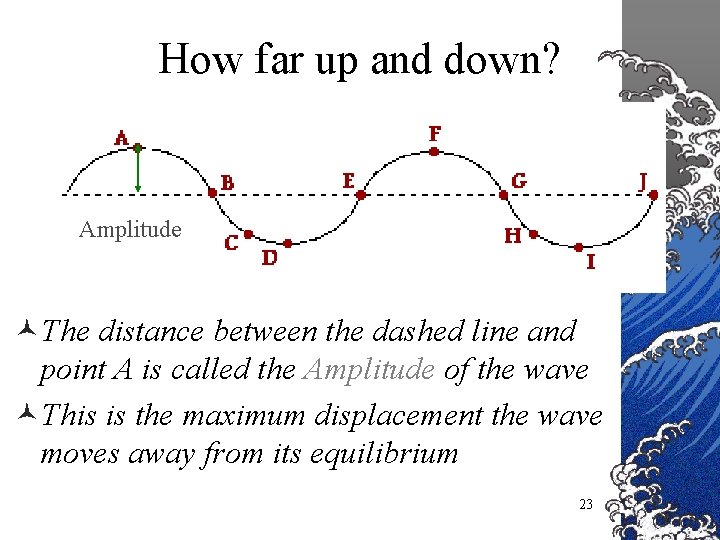
How far up and down? Amplitude ©The distance between the dashed line and point A is called the Amplitude of the wave ©This is the maximum displacement the wave moves away from its equilibrium 23

What length is it? wavelength © The distance between two consecutive similar points (moving in the same direction) is called the wavelength © This is the length of the wave pulse © Use the ruler verify the wavelength definition (start with crest to crest as shown, but investigate 24 what other points could be used as well)

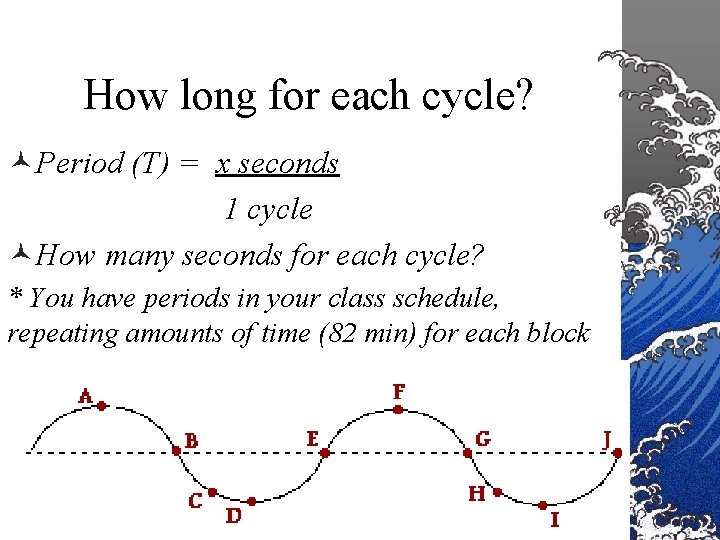
How long for each cycle? ©Period (T) = x seconds 1 cycle ©How many seconds for each cycle? * You have periods in your class schedule, repeating amounts of time (82 min) for each block 25

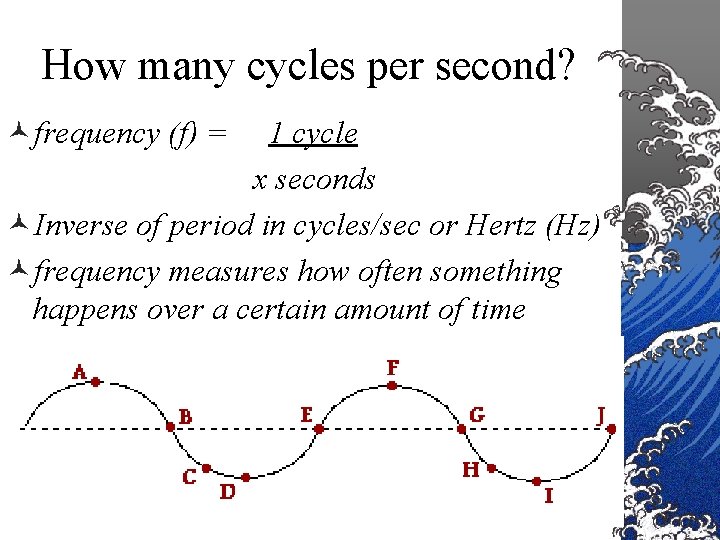
How many cycles per second? ©frequency (f) = 1 cycle x seconds ©Inverse of period in cycles/sec or Hertz (Hz) ©frequency measures how often something happens over a certain amount of time 26

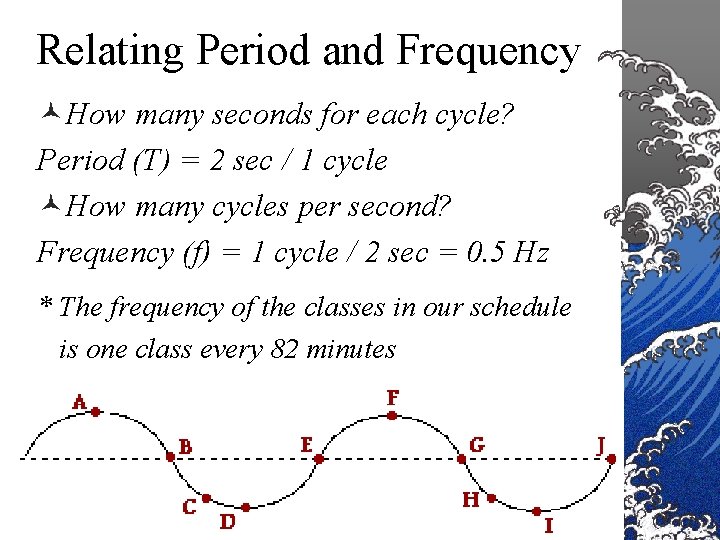
Relating Period and Frequency ©How many seconds for each cycle? Period (T) = 2 sec / 1 cycle ©How many cycles per second? Frequency (f) = 1 cycle / 2 sec = 0. 5 Hz * The frequency of the classes in our schedule is one class every 82 minutes 27

Anatomy of a Wave ©We know the cycle of the disturbance will determine the parts of the wave ©We know that things that repeat have a frequency and a period ©Still have questions? Watch the video to learn more about the anatomy of a wave 28

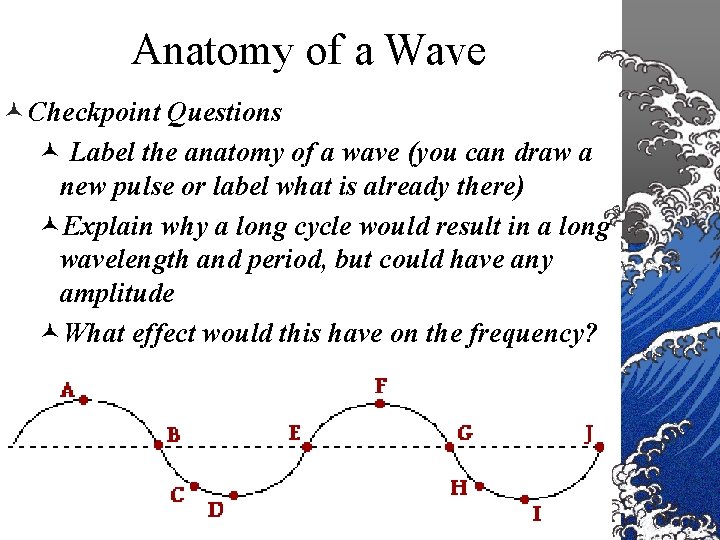
Anatomy of a Wave © Checkpoint Questions © Label the anatomy of a wave (you can draw a new pulse or label what is already there) ©Explain why a long cycle would result in a long wavelength and period, but could have any amplitude ©What effect would this have on the frequency? 29

Wave Speed ©We can use what we know to determine how fast a wave is moving ©What is the formula for velocity? ©velocity = distance / time ©What distance do we know about a wave ©wavelength ©and what time do we know about a wave ©period 30

Wave Speed ©so if we plug these in we get ©velocity = length of pulse / time for pulse v= /T v = velocity (m/s) l = wavelength (m) T = period (s) 31

Wave Speed ©v = / T but what does T equal? ©T = 1 / f ©So we can also write ©v = f ©velocity = frequency * wavelength ©This is known as the wave equation 32

Wave Speed © Checkpoint Questions © Explain the effect on velocity from… ©Increased wavelength ©Increased period ©Increased frequency ©Increased amplitude ©Recall the cycle you used to create a wave pulse. Justify which part of this cycle (and therefore which wave part) is most directly responsible for the amount of energy transferred by a wave. 33