Waves and Sound Remember Periodic Motion Motion which

�Waves and Sound

Remember Periodic Motion? • Motion which repeats in a regular cycle • Pendulum, vibrating spring, vibrating guitar string

Simple Harmonic Motion • Motion around a point of equilibrium • Force proportional to displacement of object from equilibrium

What is a wave? • Wave=disturbance that carries energy through matter or space • Note that the actual matter does not travel far but the energy can- the energy in this wave could have traveled from Alaska!

Classification of Waves Are: • Mechanical or Non-Mechanical • One (or More) Pulses or Periodic • Longitudinal or Transverse or Combined

Mechanical Waves • Require A Medium For Transmission – Medium = Mass / Atoms / Material • Transmitted Via Vibration Of Particles In The Medium Around A “Rest” Position • Examples – Sound – Water Wave

Non-Mechanical Waves • No Medium Is Required For Transmission • Can Be Transmitted Through Empty Space • Examples: – Visible Light – Infrared Or Ultraviolet Light – Radio/TV Waves Microwaves Any Electromagnetic Radiation

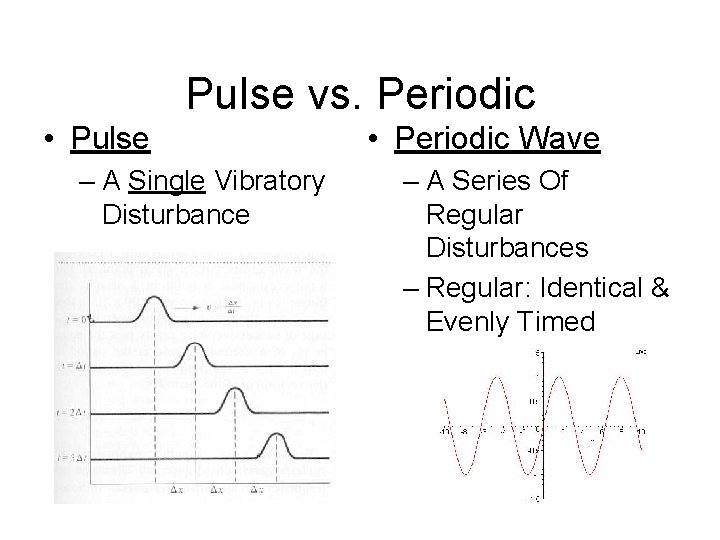
Pulse vs. Periodic • Pulse – A Single Vibratory Disturbance • Periodic Wave – A Series Of Regular Disturbances – Regular: Identical & Evenly Timed

Transverse waves • Disturbance is perpendicular to the motion of the wave • http: //www. youtube. com/watch? v=c. PKGa 2 Ds. Is 0

Longitudinal Waves • Disturbance is parallel to motion of wave • Ex- sound waves • Fluids usually only transmit longitudinal waves

Surface Waves/ Elliptical Waves • Underwater, waves are longitudinal but at the surface they have elements of both longitudinal and transverse • Motion of a particle on the surface is an ellipse

Torsional Waves • Twist around a central axis • Like Tacoma Narrows Bridge

Wave properties • • Equilibrium Crest Trough Amplitude • Phase • Wavelength

Amplitude • Maximum displacement of a particle in a wave from the equilibrium • Examples: brightness of a light, loudness of a sound

Wavelength • Distance between 2 corresponding locations • Usually measured from crest to crest or trough to trough • Symbol is

Amplitude and Wavelength • These waves have the same wavelength but different amplitudes • These waves have the same amplitude but different wavelengths

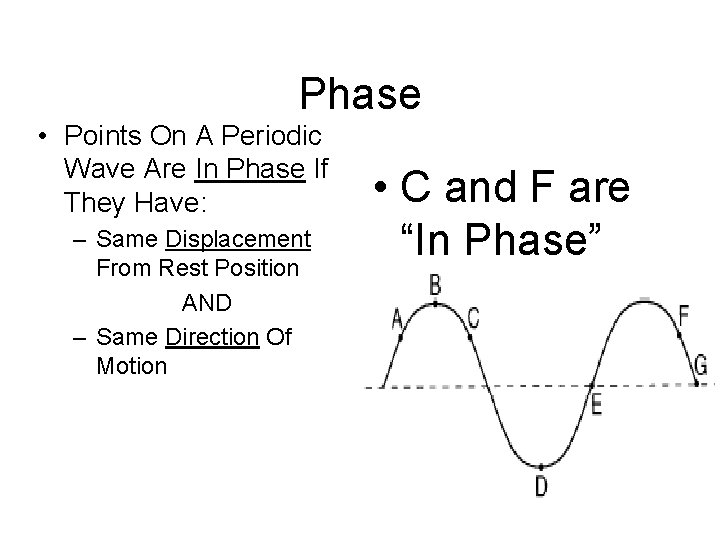
Phase • Points On A Periodic Wave Are In Phase If They Have: – Same Displacement From Rest Position AND – Same Direction Of Motion • C and F are “In Phase”

Phase • Points that are “in phase” act the same - they are a whole multiple of a wave apart • Since wavelength is one complete cycle, we usually refer to it as 360 • So in phase= n 360 • Points that are “out of phase” are not a whole multiple of 360 apart- they can be any # of degrees apart • We usually look at 90 , 180 , and 270 apart

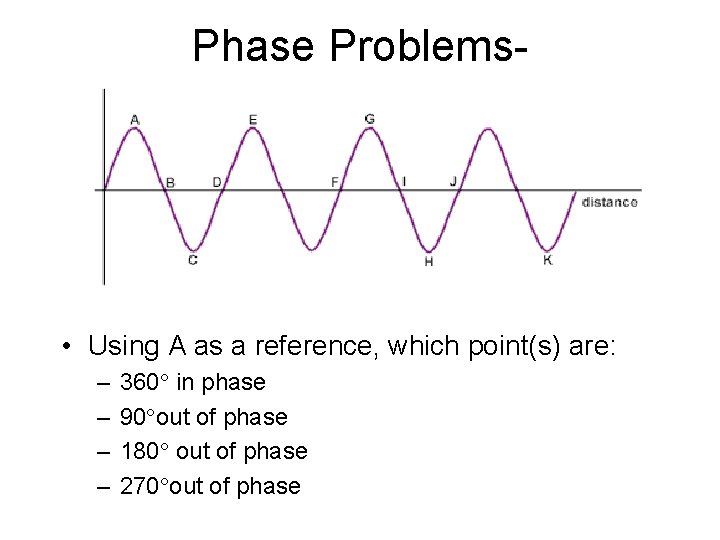
Phase Problems- • Using A as a reference, which point(s) are: – – 360 in phase 90 out of phase 180 out of phase 270 out of phase

Frequency • Number of vibrations per second • Symbol is f • Unit is Hz (1/s)

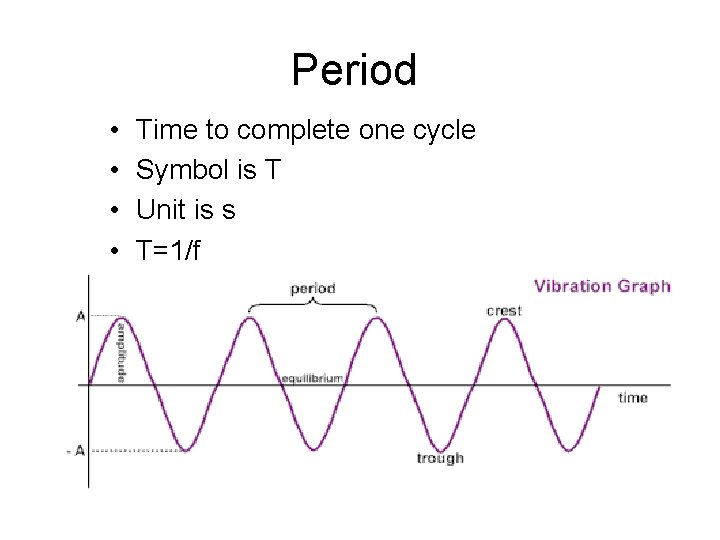
Period • • Time to complete one cycle Symbol is T Unit is s T=1/f

Speed • Speed of a wave= wavelength x frequency • v= f • Examples- we see the baseball hit the bat before we hear it b/c light wave travels faster than sound wave

Comparing Wave Speeds • Light: 3. 00 x 108 m/s • Sound: 3. 31 x 102 m/s • We See The Lightning Flash Before We Hear The Thunder. • We See The Bat Hit The Ball Before The Crack Is Heard

Speed of a Wave on a String • For faster waves: tighter string (more tension) or lighter string (less mass per length) • Mass/length is known as the linear mass density

Speed of wave problems • A ball of string is purchased at a local hardware store. According to the manufacturer, the package contains 100 yards (91. 5 meters) of string and has a mass of 12 oz (341 grams) • What is the string's linear mass density? • If the string's tensile strength is 90 N, what is the maximum speed a pulse could travel along the string?

solutions • Mass/length= 3. 73 x 10 -3 kg/meter • Speed=155. 3 m/sec

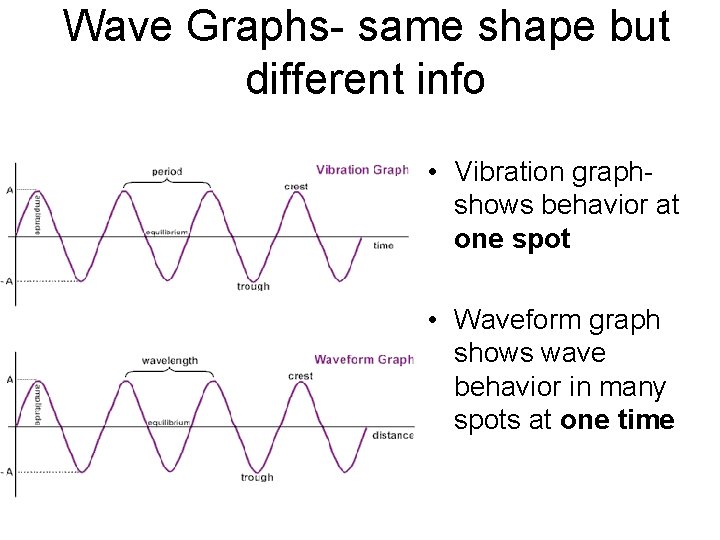
Wave Graphs- same shape but different info • Vibration graphshows behavior at one spot • Waveform graph shows wave behavior in many spots at one time

Problems • A periodic wave goes through twenty complete cycles of its motion in 4. 0 seconds • What is the frequency of the wave? • What is its period? • Determine the frequency of a wave whose period is 5. 0 seconds

Wavefront • The Locus Of Adjacent Points Which Are In Phase – Such As The Crest Of A Water Wave

Spherical Wavefront

Spherical Wavefront

Periodic Wave Phenomena • Superposition/Interference • Resonance • Doppler Effect • Diffraction • Reflection • Refraction

Waves at An Interface • Interface – A Boundary With A Different Medium • Part Of The Wave Is Reflected • Part Is Transmitted Through The Second Medium • Part Is Absorbed (Turns Into Heat) • Speed can change

Reflection At a rigid boundary, when wave hits with an upward force, the boundary medium will react with a downward force so reflected wave is INVERTED • If boundary is nonrigid (it can move) wave will reflect in same orientation

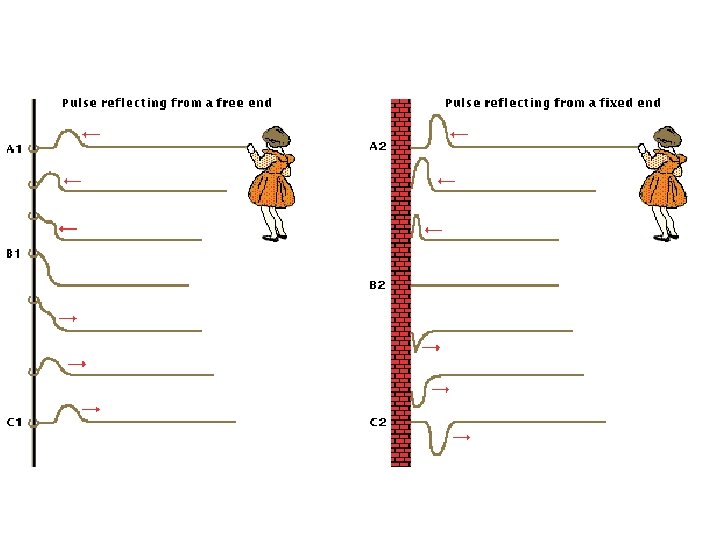
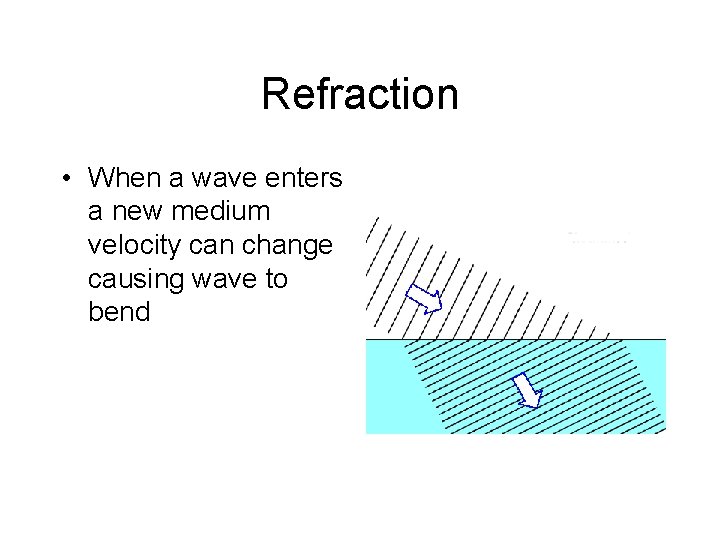
Refraction • When a wave enters a new medium velocity can change causing wave to bend

Doppler Effect • A Variation In Observed Frequency When There Is Relative Motion Between A Source And An Observer • Approaching: – Higher Frequency Observed • Receding – Lower Frequency Observed n Sound n n Pitch Changes Light n Color Changes

Doppler Effect Examples Siren Passing

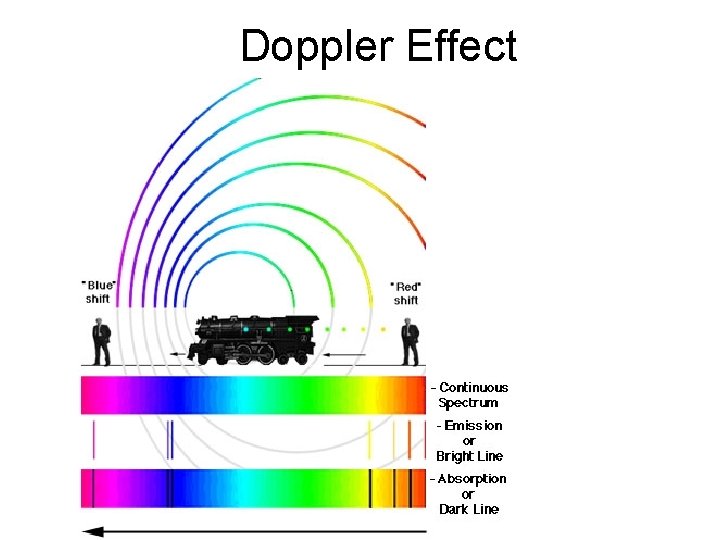
Doppler Effect

Calculations involving Doppler Effect • Let fs be the source frequency and fd be the detected frequency • If source moving towards you, frequency will increase so choose + or - accordingly – fd=(v+vd)/(v+vs) *fs • Thus, if moving away, frequency will be lower • If moving towards, frequency will be higher

Example: Doppler • A car is traveling 20 m/s away from a stationary observer. If the car’s horn emits a frequency of 600 Hz, what frequency will the observer hear? • Use v=340 m/s for the speed of sound

Solution • Since car is traveling away from observer, frequency will be lower • fd=(340+0)/(340+20) * 600 Hz= 567 Hz

Breaking the sound barrier • Speed of sound varies in different mediums • When something travels faster than the local speed of sound it “breaks the sound barrier”

Breaking the sound barrier Regions of constructive interference=SHOCK WAVES

Superposition of waves • When 2 waves meet, the displacement in the medium is the sum of the individual displacements • They then continue, unchanged by their meeting

Constructive Interference • Maximum Constructive Interference Occurs When The Phase Difference Is 0° “In Phase”

Destructive Interference • Maximum Destructive Interference Occurs When The Phase Difference Is 180 “Out of Phase”

Interference Patterns • Symmetrical Patterns Produced By Sources In Phase In The Same Medium

Interference Can Produce Colors

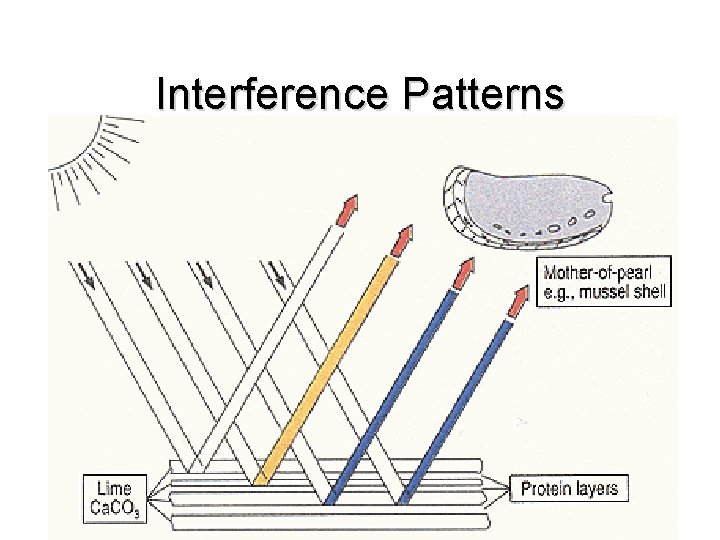
Interference Patterns

Interference Patterns • Maximum destructive interference produces nodes • Maximum constructive interference produces antinodes • http: //www. physicsclassroom. com/mmedia/waves/ipd. cfm

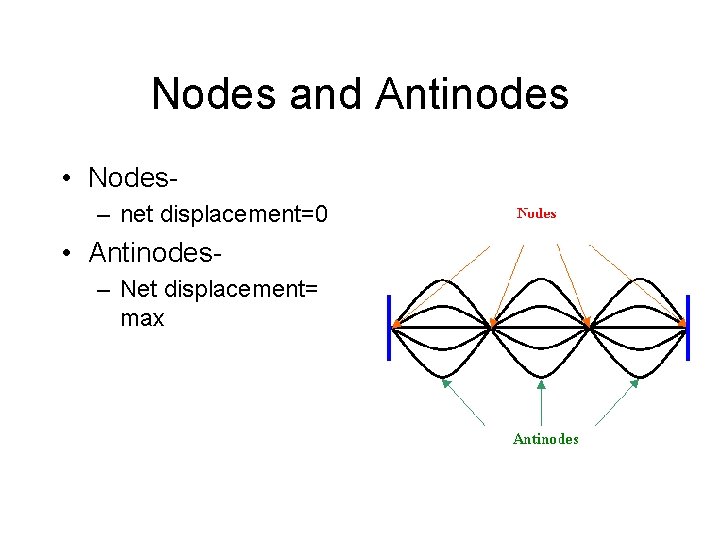
Nodes and Antinodes • Nodes– net displacement=0 • Antinodes– Net displacement= max

Nodes & Anti-Nodes • Nodes – Points of NO DISPLACEMENT • Anti-Nodes – Points of MAXIMUM DISPLACEMENT • Line of Nodes – “Smooth Area”

Standing Waves • Each object has a “natural frequency” at which it is “willing” to vibrate • If you force a vibration at this frequency, object will resonate or vibrate at increasing amplitude • Next shower, try to test this- sing different notes until you reach one that is significantly louder (increased amplitude) • We can make this using a wave reflecting off a boundary at the same frequency, amplitude, and wavelength

Resonance • If small, regular forces applied at just the right time it can increase the amplitude of vibration • Ex- trampoline, maybe Tacoma Narrows Bridge? • In a string, this depends on its length- always draw! • http: //www. ngsir. netfirms. com/englishhtm /Stat. Wave. htm

Nodes, Antinodes in Standing Waves • Nodes and antinodes alternate • Each node is 1/2 from the last • We use this to determine how standing waves form

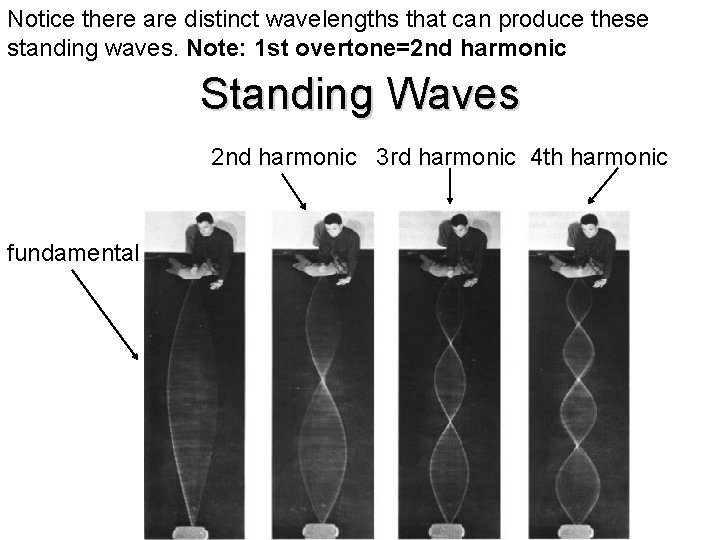
Notice there are distinct wavelengths that can produce these standing waves. Note: 1 st overtone=2 nd harmonic Standing Waves 2 nd harmonic 3 rd harmonic 4 th harmonic fundamental

Harmonics vs overtones • Let’s take a guitar string: the fundamental (also known as 1 st harmonic) is when there is λ/2 wavelengths

2 nd harmonic (1 st overtone) • The second harmonic occurs when you have twice the fundamental so 2(λ/2)=1 wavelength

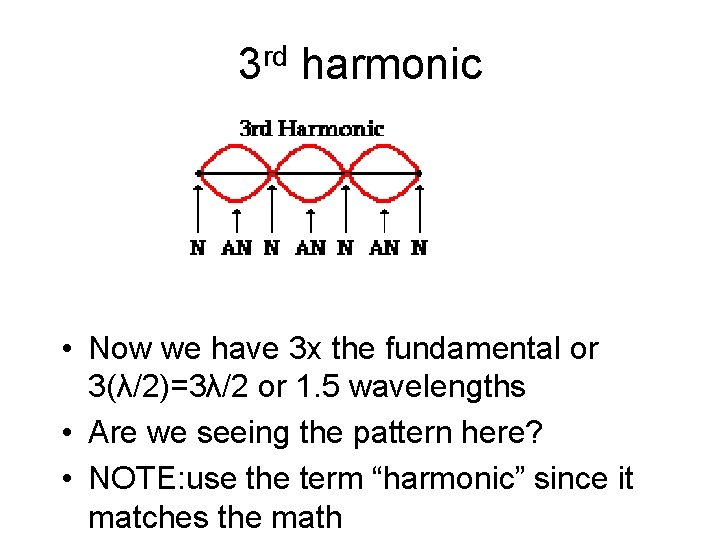
3 rd harmonic • Now we have 3 x the fundamental or 3(λ/2)=3λ/2 or 1. 5 wavelengths • Are we seeing the pattern here? • NOTE: use the term “harmonic” since it matches the math

Determining harmonic frequencies • Consider an 80 -cm long guitar string that has a fundamental frequency (1 st harmonic) of 400 Hz. • What is the wavelength of the 2 nd harmonic?

• wavelength is 160 cm or 1. 60 m. • Now what is the speed of the wave?

• speed = frequency • wavelength • speed = 400 Hz • 1. 6 mspeed = 640 m/s • Now, the speed of the other harmonics is the same- you can use their wavelengths to determine the frequency of each harmonic • What is the frequency of the 2 nd harmonic?

solution • Wavelength of 2 nd harmonic would be 0. 8 m • f=v/λ • f=640/0. 8=800 Hz • Now calculate frequency of 3 rd harmonic

Standing waves- strings • Strings are fixed on both ends • How does the fundamental frequency compare to the length of the string? • Draw the fundamental and 2 harmonics

Resonance in Strings- Probs • Two identical vibrating strings are 2. 0 meters long and uniform in density. One is fixed on both ends, the other is free on one end. • What is the wavelength of the fundamental frequency along the fixed-end string? • What is the wavelength of the fundamental frequency along the free-end string? • What is the wavelength of the first overtone along the free-end string? • What is the wavelength of the second overtone along the fixed-end string?

Resonance and Wave Speed • Now put it together with wave speed in a spring: • Suppose a string of length 100 meters has a mass of 300 grams: determine the fundamental frequency in this string when a 5 -kg mass is suspended from a 1 -meter vibrating section.

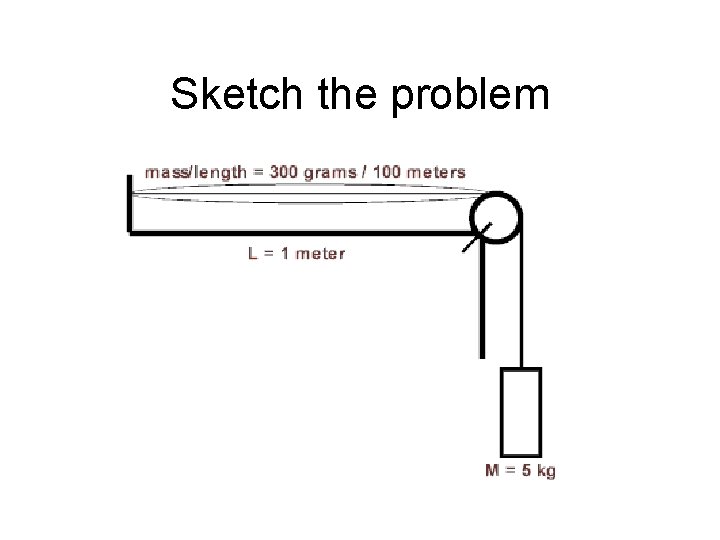
Sketch the problem

solution T = mg T = (5)(9. 81) = 49. 05 N • mass/length = 0. 3 / 100 = 3 x 10 -3 kg/m • for the fundamental, L = ½λ = 1 meter λ = 2 meters • vw = √[49. 05/(3 x 10 -3)] • vw = 127. 8 m/sec • vw = fλ • 127. 8 = f(2) • f = 63. 9 hz

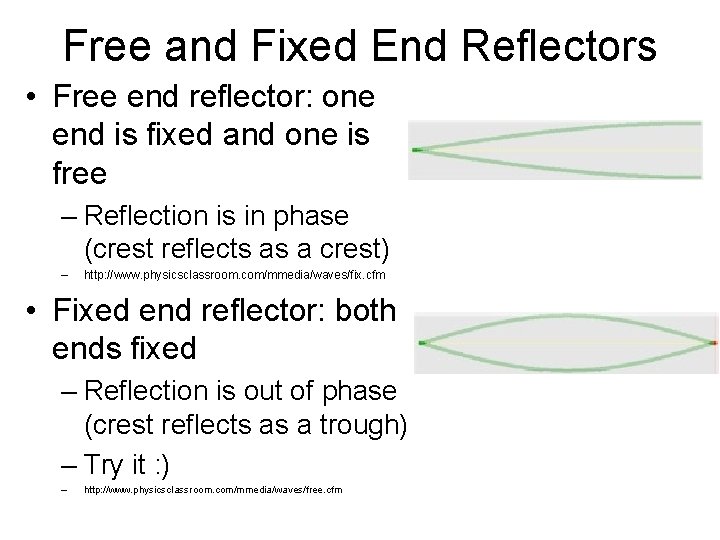
Free and Fixed End Reflectors • Free end reflector: one end is fixed and one is free – Reflection is in phase (crest reflects as a crest) – http: //www. physicsclassroom. com/mmedia/waves/fix. cfm • Fixed end reflector: both ends fixed – Reflection is out of phase (crest reflects as a trough) – Try it : ) – http: //www. physicsclassroom. com/mmedia/waves/free. cfm

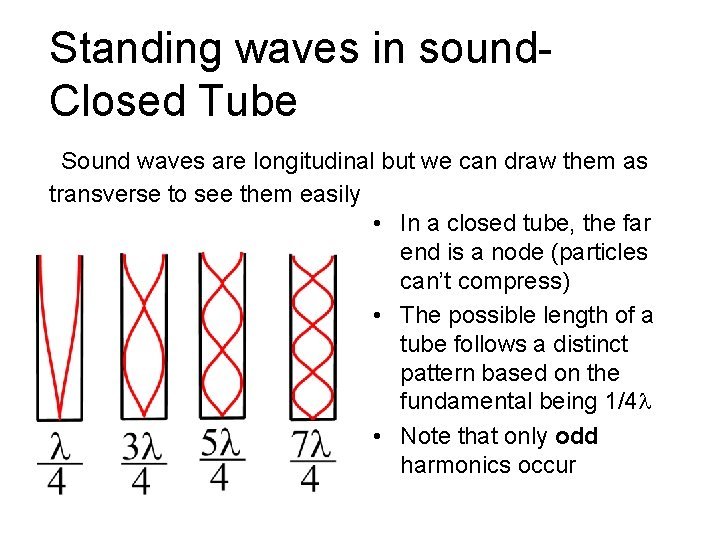
Standing waves in sound. Closed Tube Sound waves are longitudinal but we can draw them as transverse to see them easily • In a closed tube, the far end is a node (particles can’t compress) • The possible length of a tube follows a distinct pattern based on the fundamental being 1/4 • Note that only odd harmonics occur

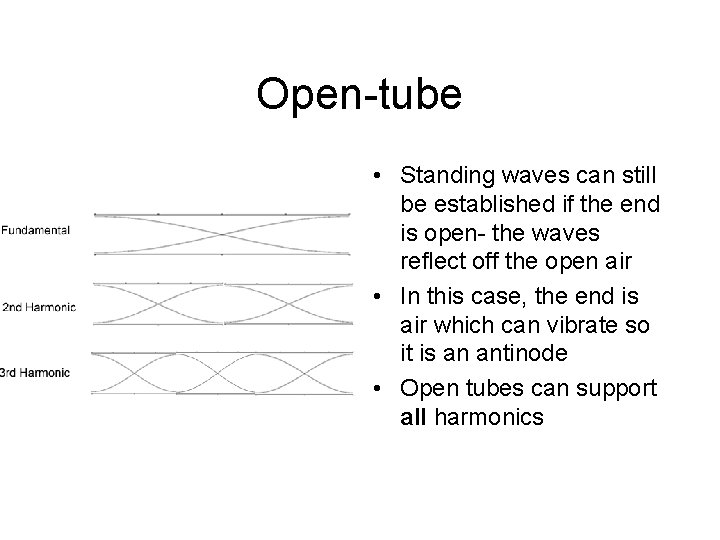
Open-tube • Standing waves can still be established if the end is open- the waves reflect off the open air • In this case, the end is air which can vibrate so it is an antinode • Open tubes can support all harmonics

Harmonics and music • String instruments often have multiple harmonics vibrating simultaneously - this produces the particular timbre of the instrument • http: //dev. physicslab. org /asp/applets/string/help. asp • The pentatonic scale-= these overtones and fundamental : • http: //www. youtube. com /watch? v=ne 6 t. B 2 Ki. Zuk

Sound Waves • Mechanical • Need a medium • No sound in space

Sound Waves • Longitudinal • Vibrations create pressure variations in medium • Compressions • Rarefactions • Feel your throat as you hum • http: //www. physicsclassroom. com/mmedia/waves/tfl. cfm

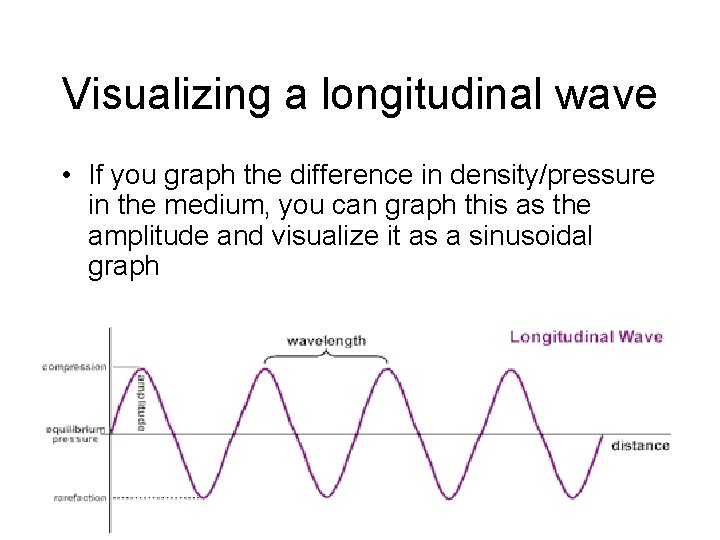
Visualizing a longitudinal wave • If you graph the difference in density/pressure in the medium, you can graph this as the amplitude and visualize it as a sinusoidal graph

Properties of sound waves • Share properties of waves • Speed v= f – Speed depends on medium and temperature • Reflection – Echo, sonar – Reflections of multiple or rough surfaces called reverberations • Interference – Dead spots(nodes) – amplification

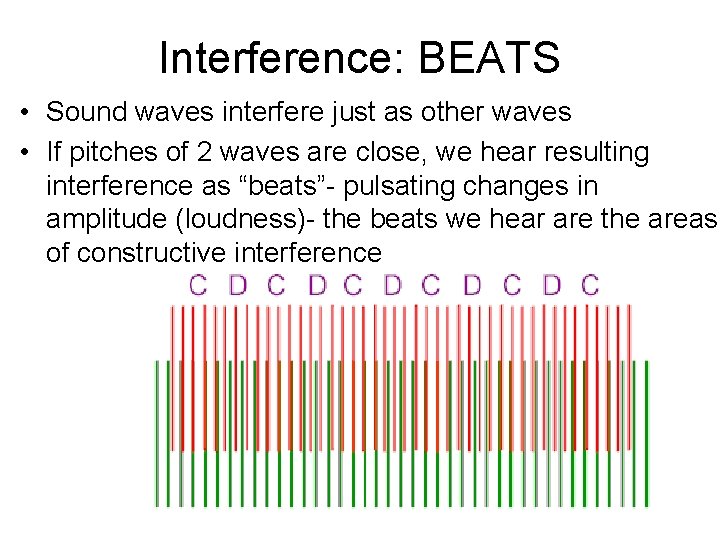
Interference: BEATS • Sound waves interfere just as other waves • If pitches of 2 waves are close, we hear resulting interference as “beats”- pulsating changes in amplitude (loudness)- the beats we hear are the areas of constructive interference

Beats Problems • Suppose you sound two tuning forks simultaneously: one fork has a frequency of 256 hz and the other has a frequency of 260 hz. – How many beats would be heard each second? – What is the pitch of these beats?

Beats • The frequency of the beats is the difference between the 2 original frequencies – beat frequency = |f 2 - f 1| • The pitch of the beats is the average of the 2 frequencies – beat pitch = ½(f 2+f 1)

Perception of Sound • Loudness = amplitude • Measured in decibel (d. B) • Exposure to loud sounds can cause your ear to lose sensitivity

Perception of Sound • Our perception of the loudness of a sound is not directly proportional to the pressureintensity is actually logarithmic so for each 10 decibel increase, the intensity goes up 10 X • Also depends on pitch, pure tone vs. combined tones

Speed of Sound • Depends on medium – Greater elasticity= faster – Metals conduct sound quickly • Depends on temp – Hot=fast • In same medium, all sound waves travel at same speed – When band plays- all sounds reach you at same speed regardless of pitch, amplitude, instrument

Speed of Sound in Air • In dry air, speed of sound is function of temp: • vw = 331 + 0. 6 T • As air becomes more humid, speed increases • If air temp not constant, can cause refraction – When this happens with light, we see a mirage

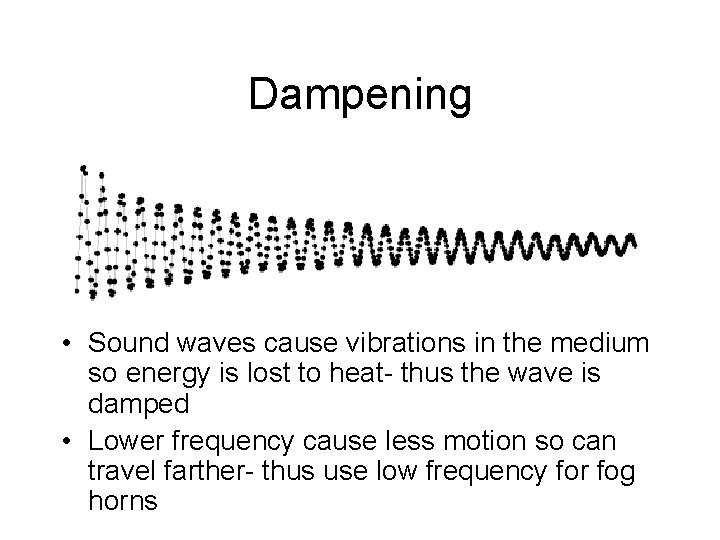
Dampening • Sound waves cause vibrations in the medium so energy is lost to heat- thus the wave is damped • Lower frequency cause less motion so can travel farther- thus use low frequency for fog horns

Physics of Music • Sound produced by vibrating object which causes pressure oscillations in air • Vibrating string • Vibrating reed(s) • Vibrating column of air