Wavelets Examples 1 Contents o Introduction o Haar

Wavelets Examples 王隆仁 1

Contents o Introduction o Haar Wavelets o General Order B-Spline Wavelets o Linear B-Spline Wavelets o Quadratic B-Spline Wavelets o Cubic B-Spline Wavelets o Daubechies Wavelets 2

I. Introduction o Wavelets are basis functions time. in continuous o A basis is a set of linearly independent functions that can be used to produce all admissible functions (1) : o The special feature of the wavelet basis is that all functions mother wavelet are constructed from a single. 3

o A typical wavelet is compressed and shifted times. Its formula is times o The remarkable property that is achieved by many wavelets is orthogonality. The wavelets are orthogonal when their “inner products” are zero : (2) o Orthogonality leads to a simple formula for each coefficient in the expansion for. 4

o Multiply the expansion displayed in equation (1) by and integrate : (3) All other terms in the sum disappear because of orthogonality. Equation (2) eliminates all integrals of times , except the one term that has j=J and k=K. That term produces. Then is the ratio of the two integrals in equation (3). That is, 5

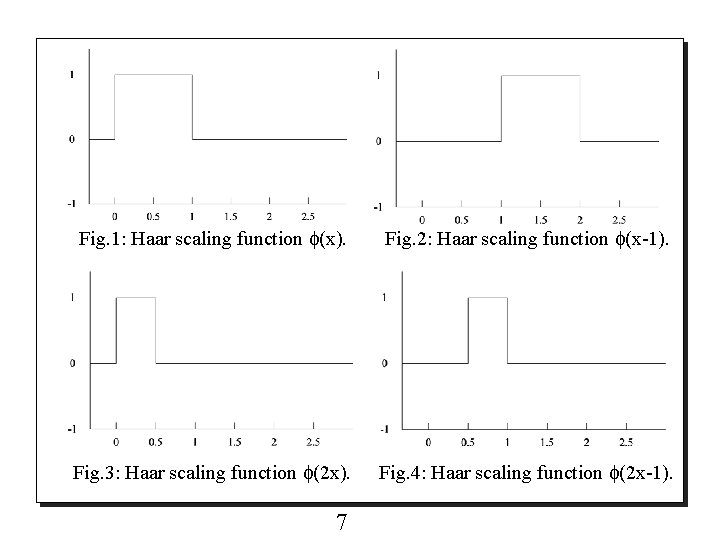
II. Haar Wavelets 2. 1 Scaling functions o Haar scaling function is defined by and is shown in Fig. 1. Some examples of its translated and scaled versions are shown in Fig. 2 -4. o The two-scale relation for Haar scaling function is 6

Fig. 1: Haar scaling function (x). Fig. 2: Haar scaling function (x-1). Fig. 3: Haar scaling function (2 x). Fig. 4: Haar scaling function (2 x-1). 7

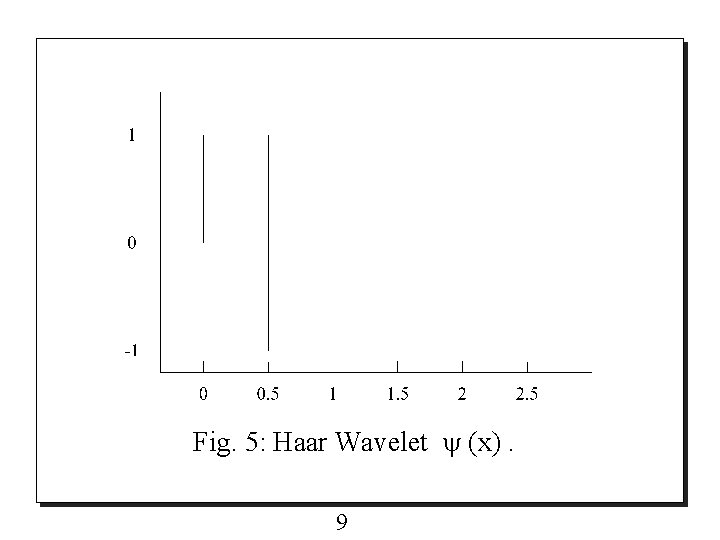
2. 2 Wavelets o The Haar wavelet (x) is given by and is shown in Fig. 5. o The two-scale relation for Haar wavelet is 8

Fig. 5: Haar Wavelet (x). 9

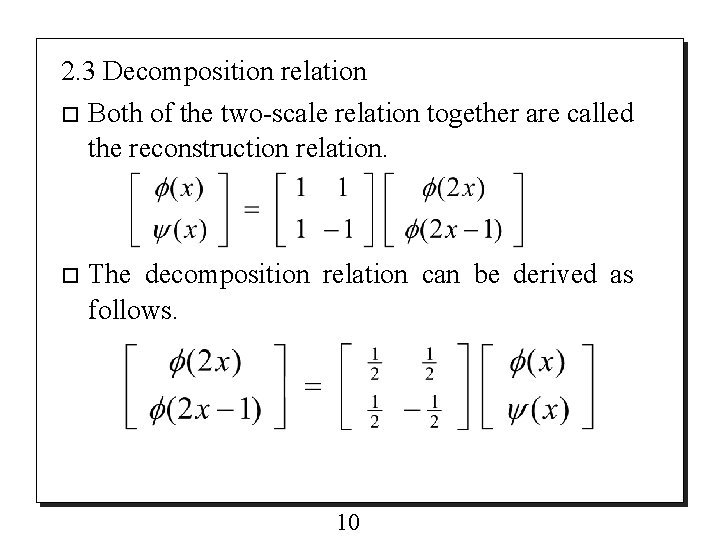
2. 3 Decomposition relation o Both of the two-scale relation together are called the reconstruction relation. o The decomposition relation can be derived as follows. 10

III. General Order B-Spline Wavelets 3. 1 Scaling functions o The m-th order B-Splines Nm is defined by (4) (5) Note that the 1 st order B-Spline N 1(x) is the Haar scaling function. 11

o The two-scale relation for B-spline scaling functions of general order m is where the two-scale sequence {pk} for B-spline scaling functions are given by : 12

3. 2 Wavelets o The two-scale relation for B-spline wavelets for general order m is given by where 13

3. 3 Decomposition relation o The decomposition relation for m-th order BSpline is where 14

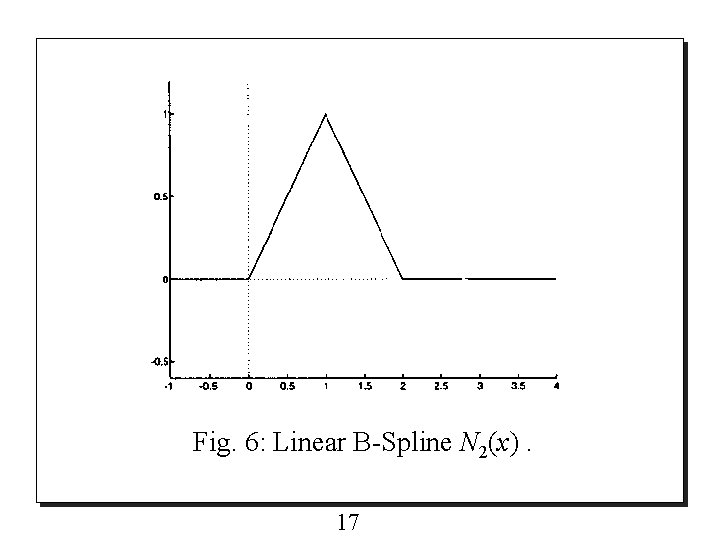
IV. Linear B-Spline Wavelets 4. 1 Scaling functions o Linear B-Spline N 2(x) is derived from the recurrence (4) and (5) as the case m=2 for general B-Splines as follows and is shown in Fig. 6. (6) 15

o Then the functions in V 1 subspace are expressed explicitly as follows and is shown in Fig. 7. (7) 16

Fig. 6: Linear B-Spline N 2(x). 17

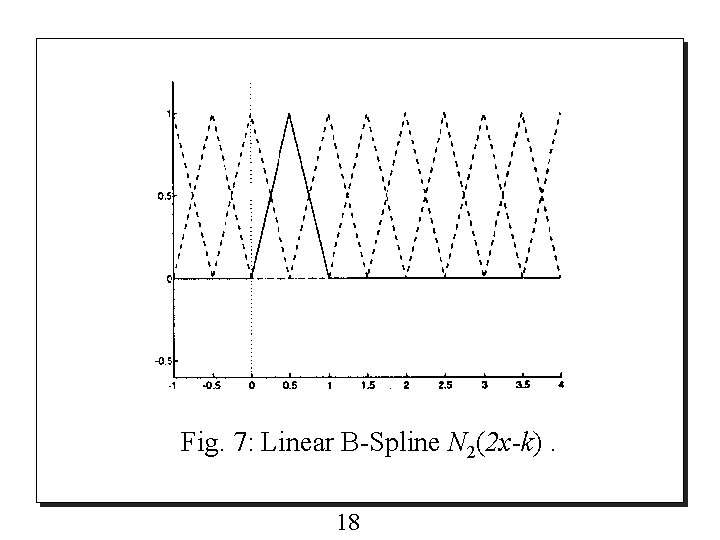
Fig. 7: Linear B-Spline N 2(2 x-k). 18

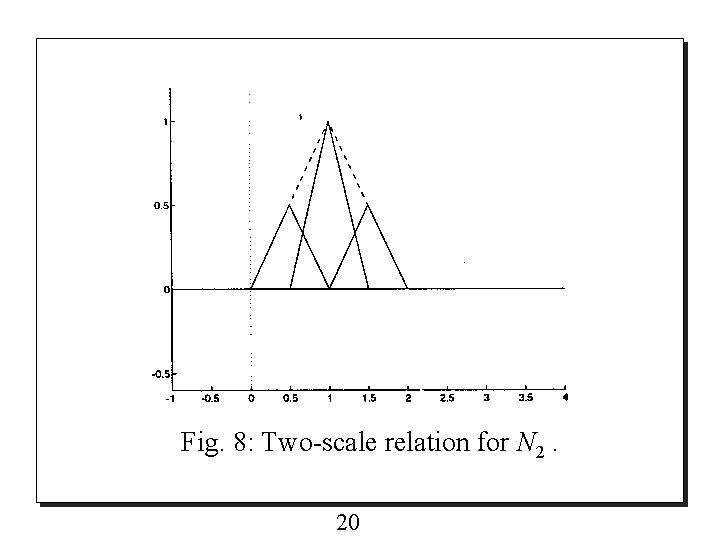
o Since the support of relation is in the form is [0, 2], its two-scale (8) o By substituting the expressions (6) and (7) for each 1/2 interval between [0, 2] into (8), the coefficients {pk} are obtained and the two scale relation for Linear B-Spline is shown in Fig. 8 and is given by 19

Fig. 8: Two-scale relation for N 2. 20

4. 2 Wavelets o The two-scale relation for Linear B-Spline wavelets for general order m=2 is where 21

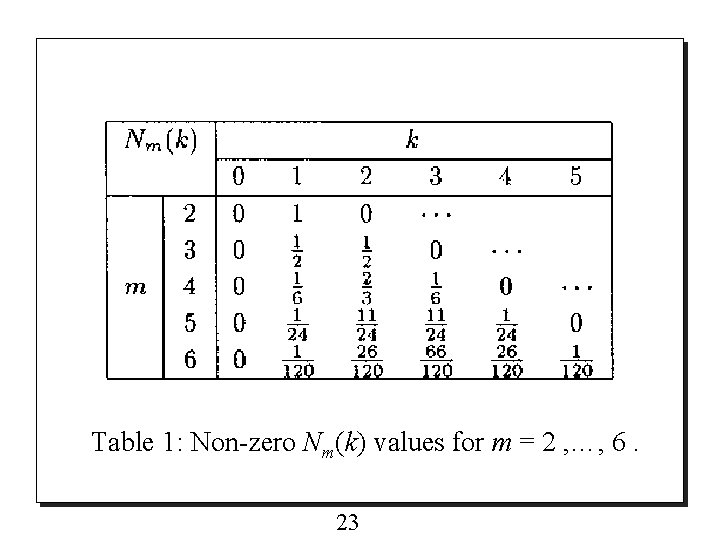
o The term N 4(k) is cubic B-spline and the recursion relation for general order B-spline is given by This relation is useful to compute Nm(k) at some integer values. Non-zero values of Nm(k) for some small m are summarized in Table 1. 22

Table 1: Non-zero Nm(k) values for m = 2 , …, 6. 23

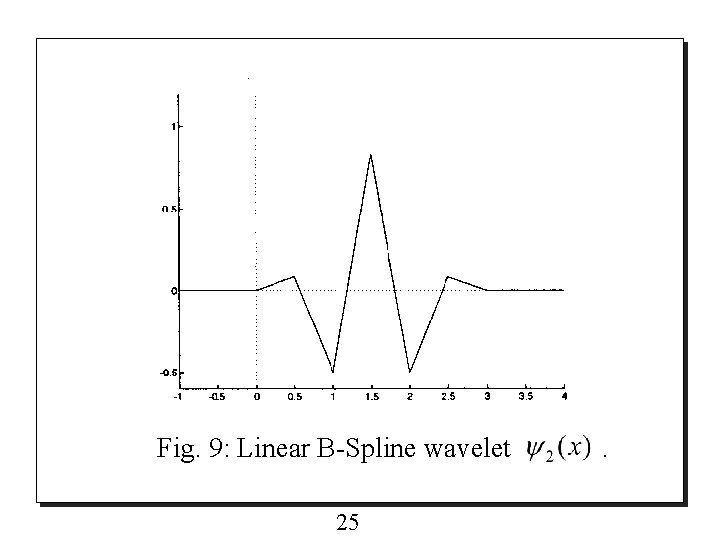
o Then the two-scale sequence {qk} for computed as follows: o Thus the Linear B-Spline wavelets is 24 is

Fig. 9: Linear B-Spline wavelet 25 .

4. 3 Decomposition relation o The decomposition sequences {ak} and {bk} are written for Linear B-Spline (m=2) as Noting that only three {pk} and five {qk} are non -zero, i. e. , and 26

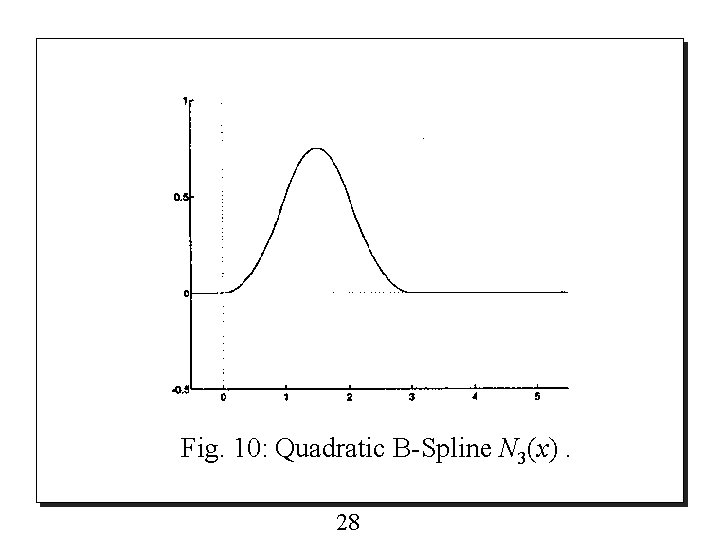
V. Quadratic B-Spline Wavelets 5. 1 Scaling functions o Quadratic B-spline N 3(x) is shown in Fig. 10 and given by 27

Fig. 10: Quadratic B-Spline N 3(x). 28

o Functions in V 1 space are expressed as 29

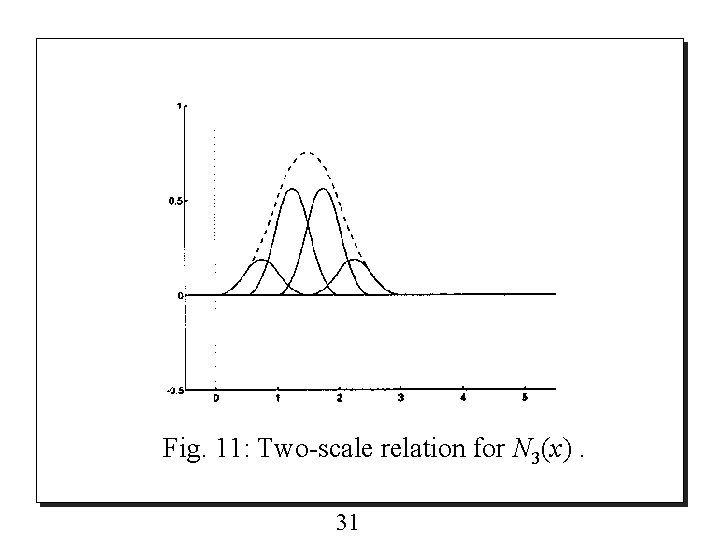
o The two-scale relation for quadratic B-Spline N 3(x) is shown in Fig. 11 and given as follow: 30

Fig. 11: Two-scale relation for N 3(x). 31

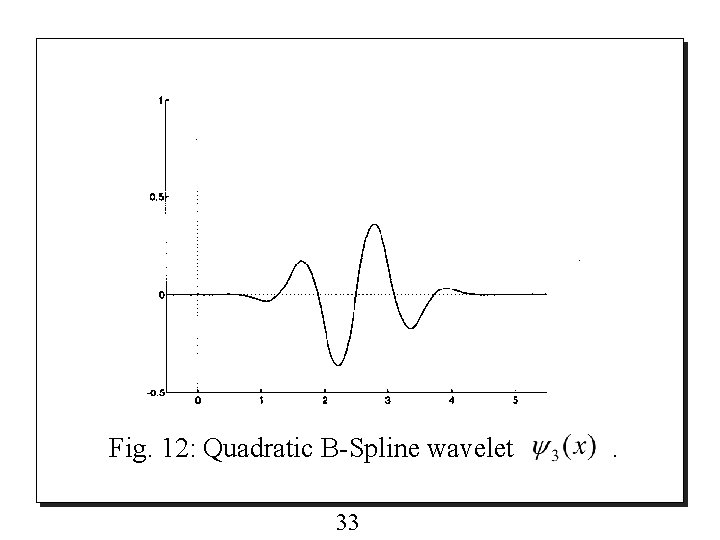
5. 2 Wavelets o The quadratic B-spline wavelet is shown in Fig. 12 and the two-scale relation is given by 32

Fig. 12: Quadratic B-Spline wavelet 33 .

5. 3 Decomposition relation o The decomposition sequences {ak} and {bk} are written for Quadratic B-Spline (m=3) as Noting that only four {pk} and eight {qk} are non -zero, i. e. , and 34

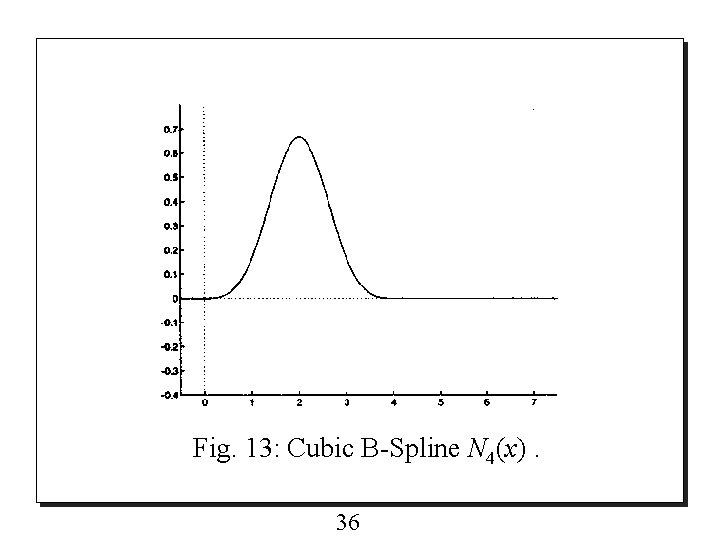
VI. Cubic B-Spline Wavelets 6. 1 Scaling functions o Cubic B-spline N 4(x) shown in Fig. 13 is given by 35

Fig. 13: Cubic B-Spline N 4(x). 36

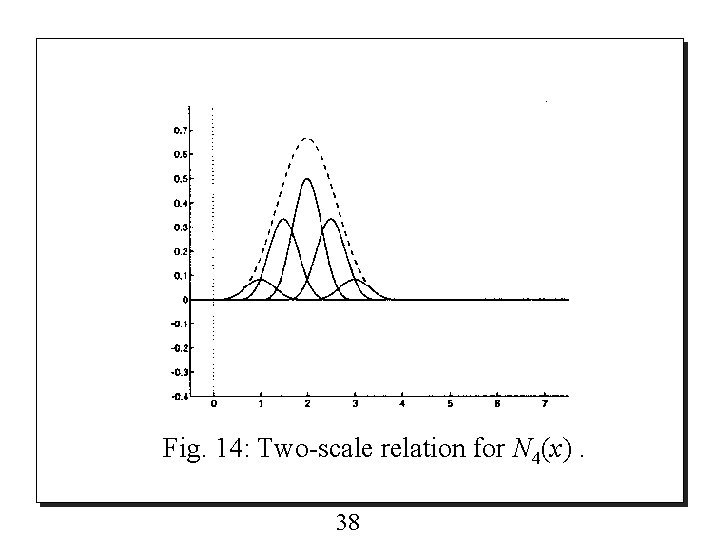
o The two-scale relation for cubic B-Spline N 4(x) is and is shown in Fig. 14. 37

Fig. 14: Two-scale relation for N 4(x). 38

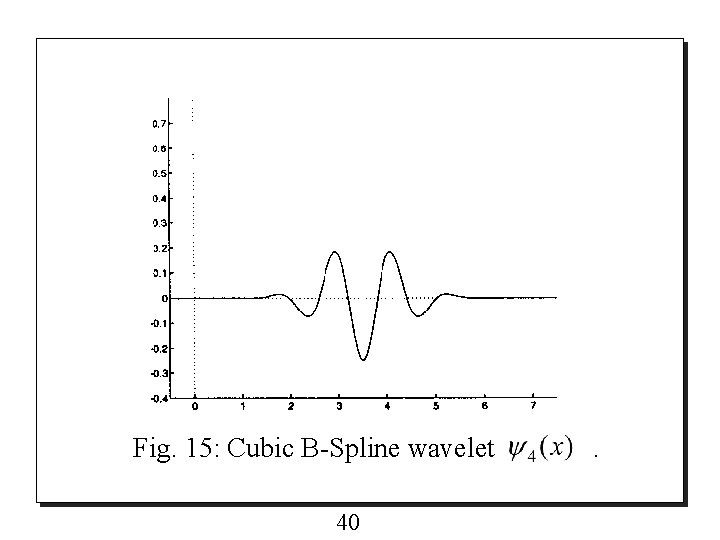
6. 2 Wavelets o The Cubic B-Spline wavelet is shown in Fig. 15. 6. 3 Decomposition relation o The decomposition sequences for Cubic BSpline are : 39

Fig. 15: Cubic B-Spline wavelet 40 .

VII. Daubechies Wavelets 7. 1 Scaling functions o Daubechies scaling function following two-scale relation : 41 is defined by the

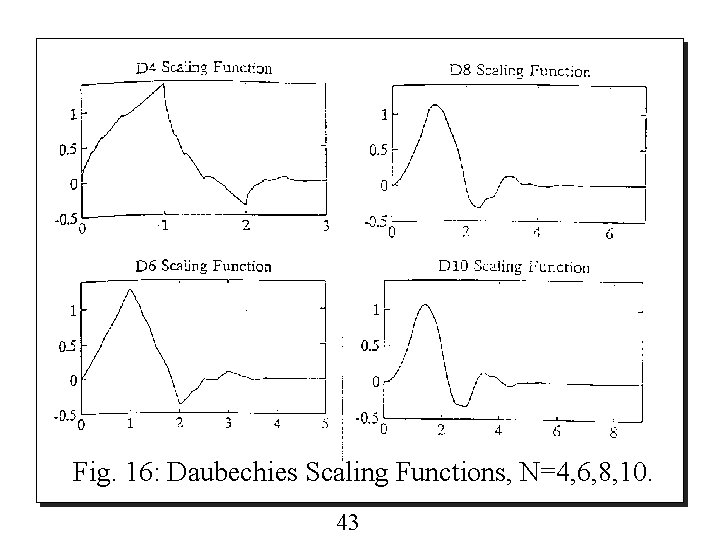
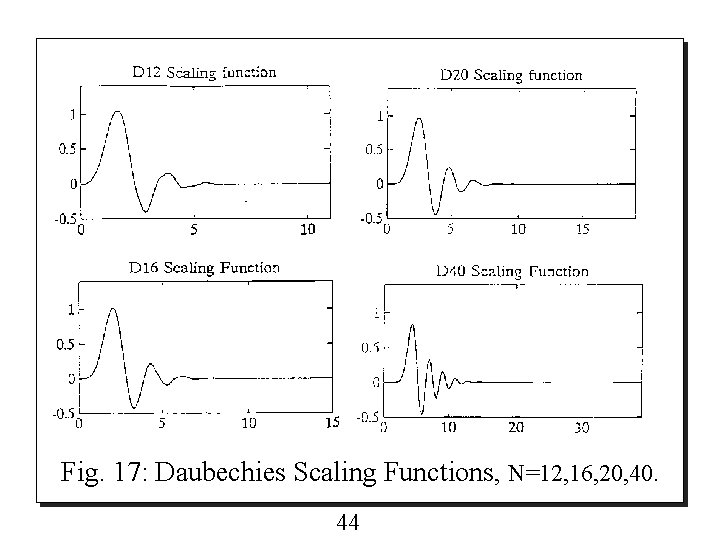
o That is, non-zero values of the two-scale sequence {pk} are : Note that the coefficients {pk} have properties p 0 + p 2 = p 1 + p 3 = 1. Figure 16 and 17 show the Daubechies scaling functions, N is the length of the coefficients. 42

Fig. 16: Daubechies Scaling Functions, N=4, 6, 8, 10. 43

Fig. 17: Daubechies Scaling Functions, N=12, 16, 20, 40. 44

7. 2 Wavelets o The two-scale relation for the Daubechies wavelets is in the following form : 45

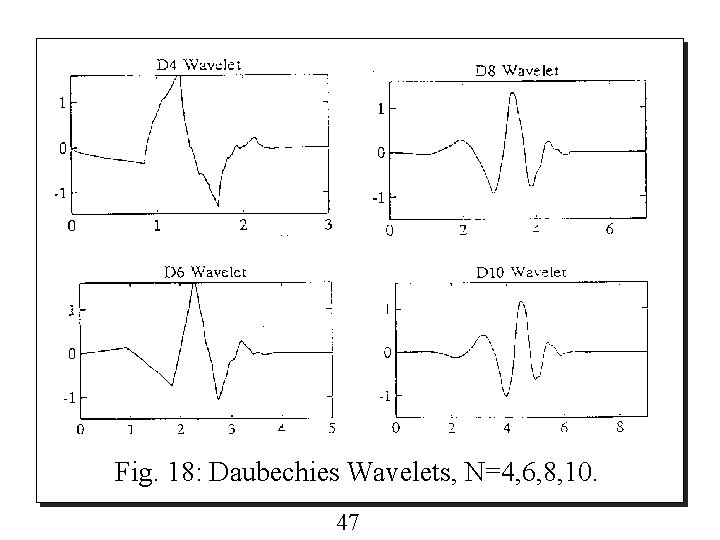
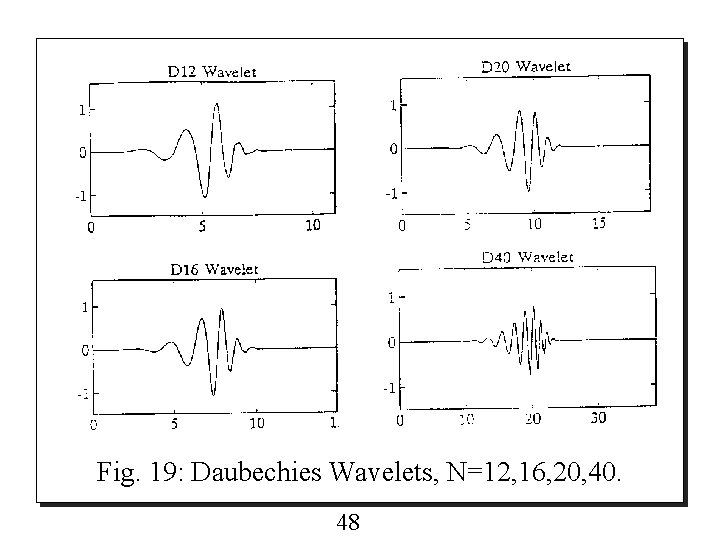
o Therefore the non-zero values of the two-scale sequence {qk} are : Figure 18 and 19 show the Daubechies wavelets, N is the length of the coefficients. 46

Fig. 18: Daubechies Wavelets, N=4, 6, 8, 10. 47

Fig. 19: Daubechies Wavelets, N=12, 16, 20, 40. 48