Wavelet domain image denoising via support vector regression

Wavelet domain image denoising via support vector regression Source: Electronics Letters, Volume: 40, Issue: 2004 PP : 1479 -1481 Authors: H. Cheng, J. W. Tian, J. Liu and Q. Z. Yu Presented by: C. Y. Gun Date: 4/7 2005 1

Outline Abstract Introduction( Mother Wavelet, Father Wavelet) Support vector regression Proposed theory and algorithm Experimental results and discussion 2

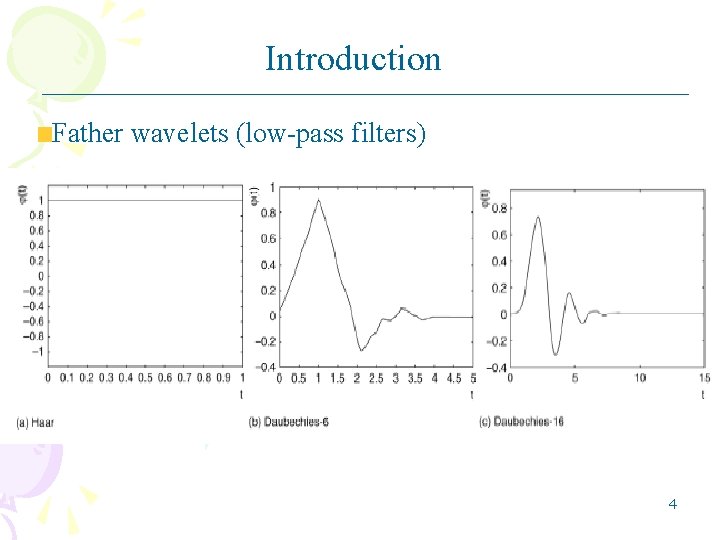
Introduction Families of Wavelets： Father wavelet ϕ(t) – generates scaling functions (low-pass filter) Mother wavelet ψ(t) –generates wavelet functions (high-pass filter) All other members of the wavelet family are scaling and translations of either the mother or the father wavelet 3

Introduction Father wavelets (low-pass filters) 4

Introduction Mother wavelets (high-pass filters) 5

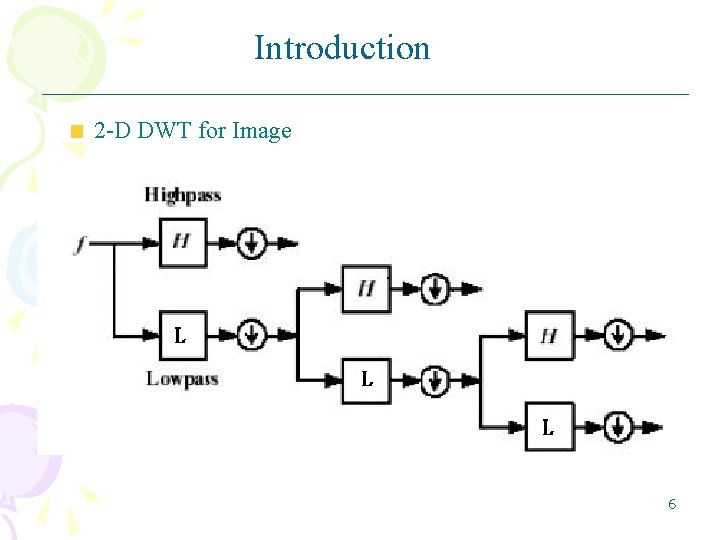
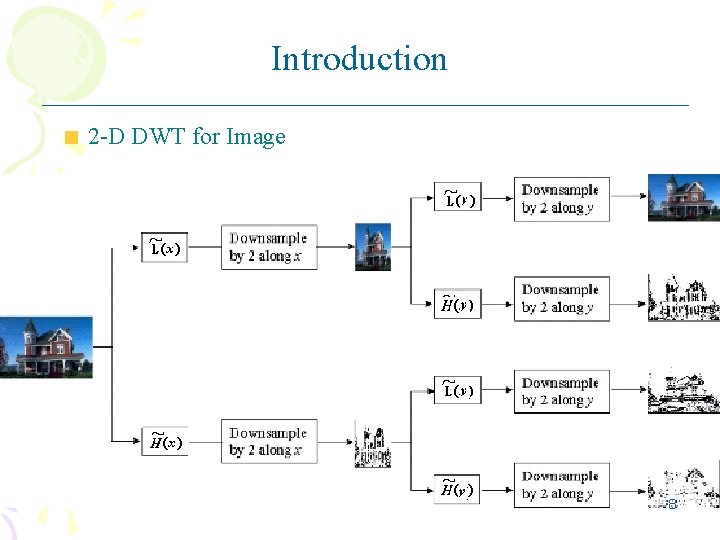
Introduction 2 -D DWT for Image 6

Introduction 2 -D DWT for Image 7

Introduction 2 -D DWT for Image 8

Support vector regression Standard linear regression equation The linear case is a special case of the nonlinear regression equation 9

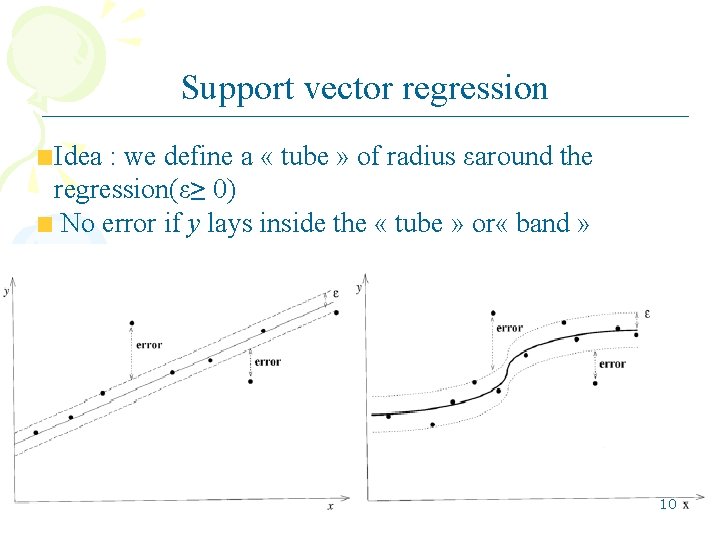
Support vector regression Idea : we define a « tube » of radius εaround the regression(ε≥ 0) No error if y lays inside the « tube » or « band » 10

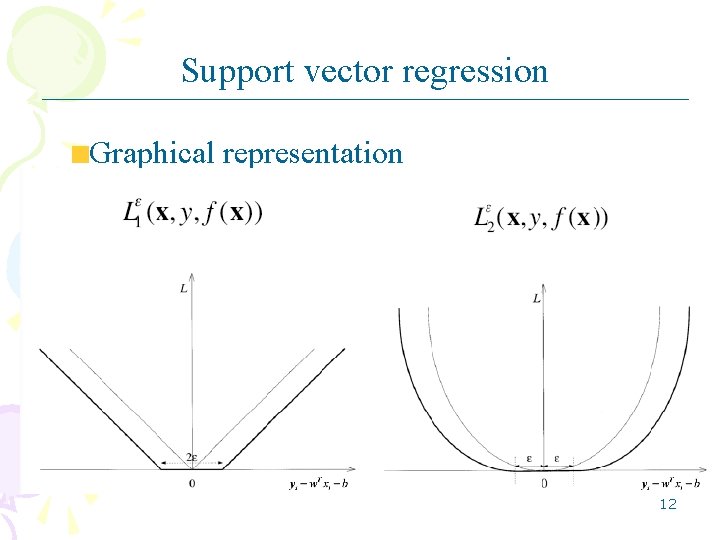
Support vector regression We therefore define an ε-insensitive loss function L 1 L 2 11

Support vector regression Graphical representation 12

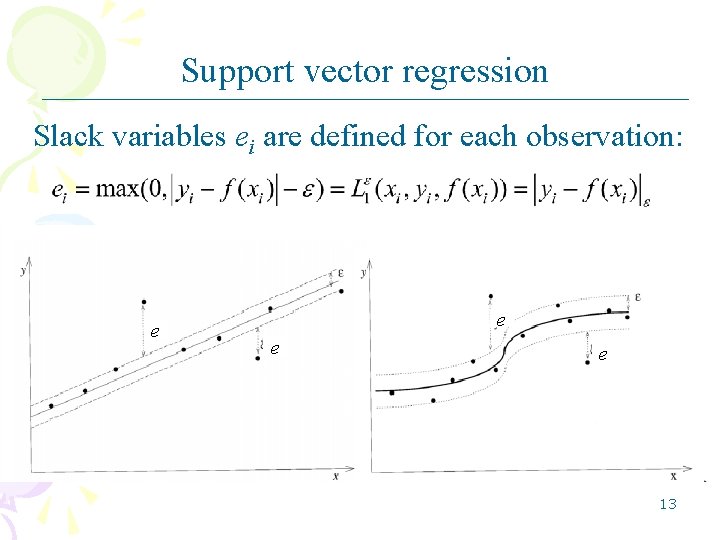
Support vector regression Slack variables ei are defined for each observation: e e 13

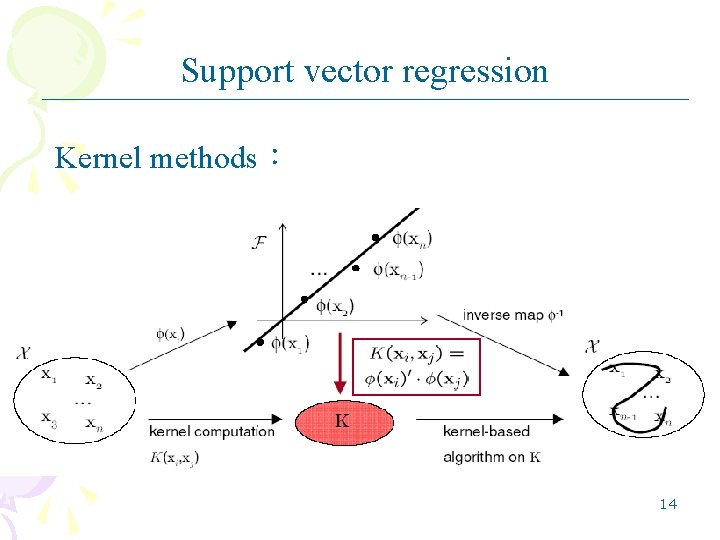
Support vector regression Kernel methods： 14

Support vector regression Basic kernels for vectorial data: – Linear kernel: (feature space is Q-dimensional if Q is the dim of ; Map is identity!) – RBF-kernel: (feature space is infinite dimensional) – Polynomial kernel of degree two: (feature space is d(d+1)/2 －dimensional if d is the dim of ) 15

LS－SVM Regression We define the following optimization problem: Or: 16

LS－SVM Regression From Least squares support vector machine classifiers …. (1) 17

LS－SVM Regression The Result LS-SVM model for function estimation is …. (2) 18

LS－SVM Regression 19

LS－SVM Regression (1) …. (3) 20

Proposed theory and algorithm Block matrix decompositions The main formula we need concerns the inverse of a block matrix =? ? 21

Proposed theory and algorithm = = where 22

Proposed theory and algorithm (3) 23

Proposed theory and algorithm 24

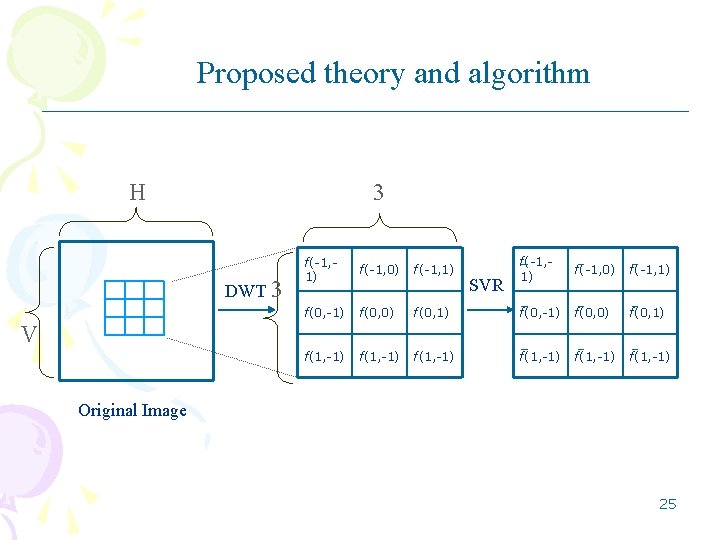
Proposed theory and algorithm H 3 DWT 3 f(-1, 1) f(-1, 0) f(-1, 1) f(0, -1) f(0, 0) f(0, 1) f(1, -1) f(-1, 0) f(-1, 1) f(0, -1) f(0, 0) f(1, -1) SVR V Original Image 25

Proposed theory and algorithm where fm is the modified wavelet coefficient, p=0. 3×max( f ). Max( f ) is the maximal value of the wavelet coefficient in that detail subband. 26

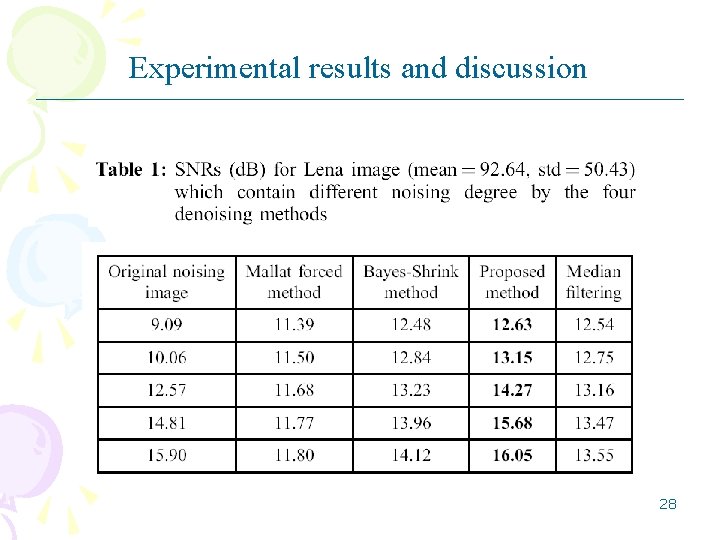
Experimental results and discussion 27

Experimental results and discussion 28

Reference • 1 Mallat, S. G. : ‘A theory for multiresolution signal decomposition: the wavelet representation’, IEEE Trans. Pattern Anal. Mach. Intell. , 1989, 11, (7), pp. 674– 693 • 2 Donoho, D. L. , and Johnstone, I. M. : ‘Ideal spatial adaptation via waveletshrinkage’, Biometrica, 1994, 81, pp. 425– 455 • 3 Chang, S. G. , Yu, B. , and Vetterli, M. : ‘Adaptive wavelet thresholding forimage denoising and compression’, IEEE Trans. Image Process. , 2000, 9, pp. 1532– 1546 • 4 Vapnik, V. : ‘The nature of statistical learning theory’ (Springer-Verlag, New York, 1995) • 5 Suykens, J. A. K. , and Vandewalle, J. : ‘Least squares support vectormachine classifiers’, Neural Process. Lett. , 1999, 9, (3), pp. 293– 300 29