Waveform inversion by oneway wavefield extrapolation Jeff Shragge

Waveform inversion by one-way wavefield extrapolation Jeff Shragge SEP-125 pp 77 -100 jeff@sep. stanford. edu

Motivation: Waveform Inversion Results Extrapolation Work Flow • 2004 BP synthetic velocity model jeff@sep. stanford. edu

Motivation: Waveform Inversion Results Extrapolation Work Flow • 2004 BP synthetic velocity model • Initial velocity model (ray tomography) jeff@sep. stanford. edu

Motivation: Waveform Inversion Results Extrapolation Work Flow • 2004 BP synthetic velocity model • (Blindly) Recovered velocity model (Pratt and Brenders) (different color scale) jeff@sep. stanford. edu

Motivation: Waveform Inversion Results Extrapolation Work Flow • 2 D Frequency domain waveform inversion – Transmission wavefield (e. g. diving and refracted arrivals) contain useful velocity model information – Set up inverse problem for minimizing differences between modeled and acquired transmission waveforms jeff@sep. stanford. edu

Motivation: Waveform Inversion Results Extrapolation Work Flow • 2 D Frequency domain waveform inversion – Transmission wavefield (e. g. diving and refracted arrivals) contain useful velocity model information – Set up inverse problem for minimizing differences between modeled and acquired transmission waveforms • BP synthetic results – Good: top salt delineation; near-surface lens recovery jeff@sep. stanford. edu

Motivation: Waveform Inversion Results Extrapolation Work Flow • 2 D Frequency domain waveform inversion – Transmission wavefield (e. g. diving and refracted arrivals) contain useful velocity model information – Set up inverse problem for minimizing differences between modeled and acquired transmission waveforms • BP synthetic results – Good: top salt delineation; near-surface lens recovery • Extension to 3 D data and model volumes? jeff@sep. stanford. edu
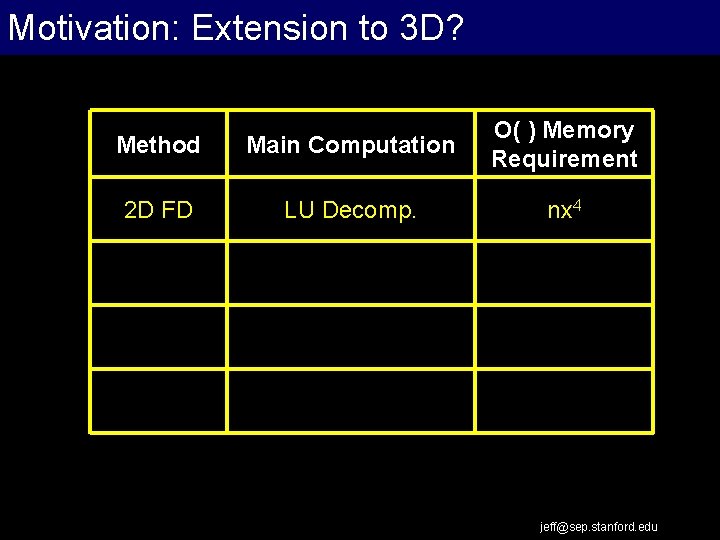
Motivation: Extension to 3 D? Extrapolation Work Flow Method Main Computation O( ) Memory Requirement 2 D FD LU Decomp. nx 4 jeff@sep. stanford. edu
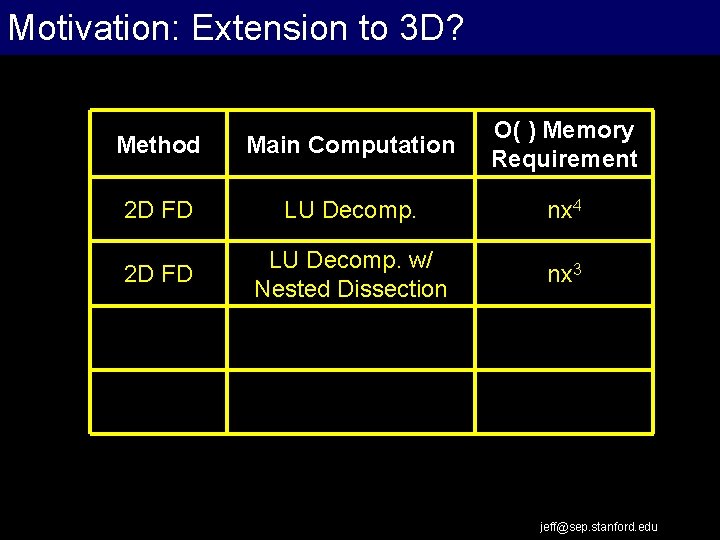
Motivation: Extension to 3 D? Extrapolation Work Flow Method Main Computation O( ) Memory Requirement 2 D FD LU Decomp. nx 4 2 D FD LU Decomp. w/ Nested Dissection nx 3 jeff@sep. stanford. edu
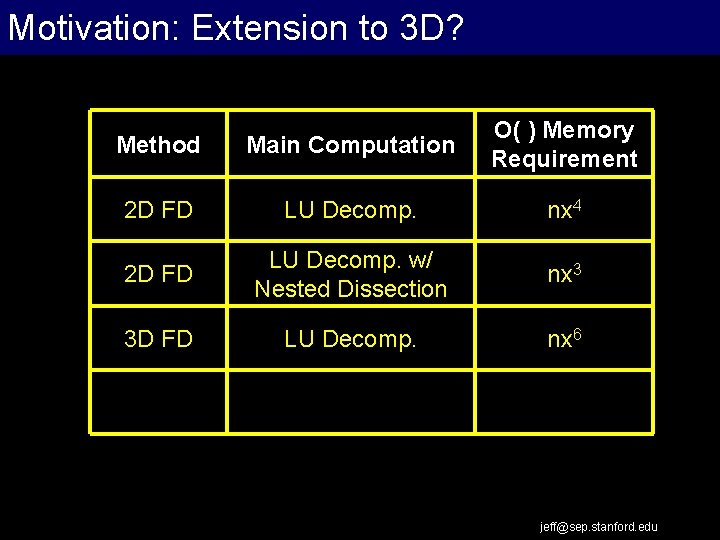
Motivation: Extension to 3 D? Extrapolation Work Flow Method Main Computation O( ) Memory Requirement 2 D FD LU Decomp. nx 4 2 D FD LU Decomp. w/ Nested Dissection nx 3 3 D FD LU Decomp. nx 6 jeff@sep. stanford. edu
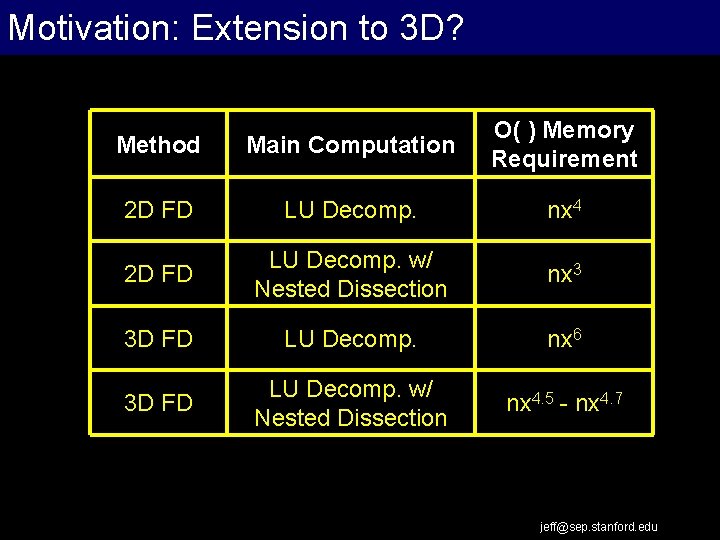
Motivation: Extension to 3 D? Extrapolation Work Flow Method Main Computation O( ) Memory Requirement 2 D FD LU Decomp. nx 4 2 D FD LU Decomp. w/ Nested Dissection nx 3 3 D FD LU Decomp. nx 6 3 D FD LU Decomp. w/ Nested Dissection nx 4. 5 - nx 4. 7 jeff@sep. stanford. edu

Motivation: Extension to 3 D? Extrapolation Work Flow • LU decomposition too expensive for 3 D problems • How do we implement waveform inversion on typical 3 D data volumes? – Reduce: Data volume? Model resolution? Physics? Inversion cost? • Alternative to FD forward modeling: – One-way wavefield extrapolation jeff@sep. stanford. edu

Motivation: Extension to 3 D? Extrapolation Work Flow • LU decomposition too expensive for 3 D problems • How do we implement waveform inversion on typical 3 D data volumes? – Reduce: Data volume? Model resolution? Physics? Inversion cost? • Alternative to FD forward modeling: – One-way wavefield extrapolation jeff@sep. stanford. edu

Motivation: Extension to 3 D? Extrapolation Work Flow • LU decomposition too expensive for 3 D problems • How do we implement waveform inversion on typical 3 D data volumes? – Reduce: Data volume? Model resolution? Physics? Inversion cost? • Alternative to FD forward modeling: – One-way wavefield extrapolation jeff@sep. stanford. edu
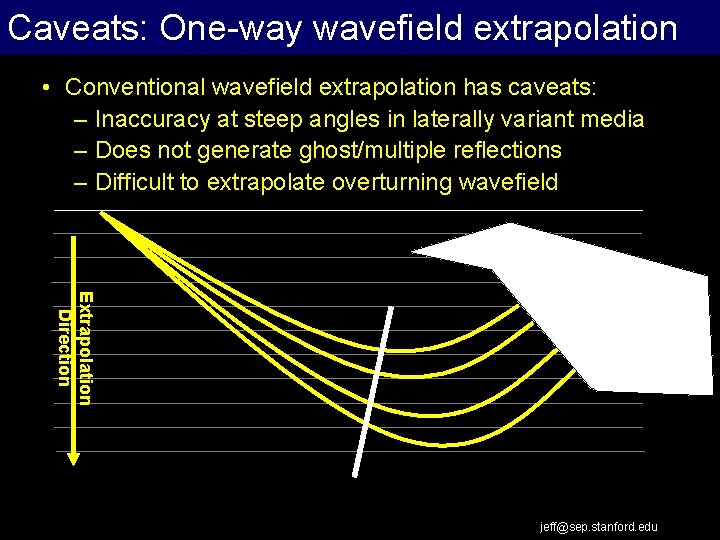
Caveats: One-way wavefield Extrapolation Work Flow extrapolation • Conventional wavefield extrapolation has caveats: – Inaccuracy at steep angles in laterally variant media – Does not generate ghost/multiple reflections – Difficult to extrapolate overturning wavefield Extrapolation Direction jeff@sep. stanford. edu
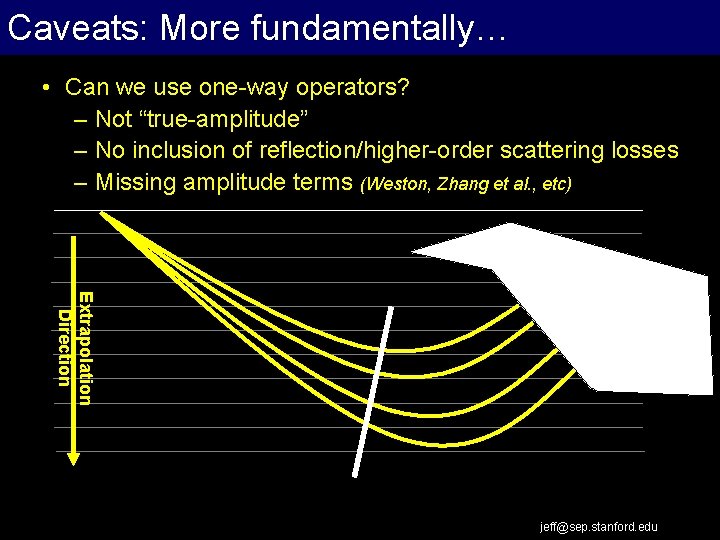
Caveats: More fundamentally… Extrapolation Work Flow • Can we use one-way operators? – Not “true-amplitude” – No inclusion of reflection/higher-order scattering losses – Missing amplitude terms (Weston, Zhang et al. , etc) Extrapolation Direction jeff@sep. stanford. edu

…but if you can. Work forward model accurately Extrapolation Flow Method Main Computation O( ) Memory Requirement 2 D FD LU Decomp. nx 4 2 D FD LU Decomp. w/ Nested Dissection nx 3 3 D FD LU Decomp. nx 6 3 D FD LU Decomp. w/ Nested Dissection nx 4. 5 - nx 4. 7 3 D WE Wavefield Extrapolation ns nx 3 (log 2 nx)2 * *Computational complexity (Biondi, 2006) jeff@sep. stanford. edu

Project: Turning-wave coordinate imaging Extrapolation Work Flow • Wavefield extrapolation on mesh oriented in turning-wave propagation direction – Turning-waves propagate at low angle to extrapolation axis • Riemannian wavefield extrapolation (RWE) (Sava and Fomel, 2005) jeff@sep. stanford. edu

Project: Turning-wave coordinate imaging Extrapolation Work Flow • Wavefield extrapolation on mesh oriented in turning-wave propagation direction – Turning-waves propagate at low angle to extrapolation axis • Riemannian wavefield extrapolation (RWE) (Sava and Fomel, 2005) jeff@sep. stanford. edu

Project: Turning-wave coordinate imaging Extrapolation Work Flow • Wavefield extrapolation on mesh oriented in turning-wave propagation direction – Turning-waves propagate at low angle to extrapolation axis • Riemannian wavefield extrapolation (RWE) (Sava and Fomel, 2005) jeff@sep. stanford. edu

Project Objectives Extrapolation Work Flow • Answer two questions: – ABSOLUTE: Is one-way wavefield extrapolation accurate enough for waveform inversion? – RELATIVE: Is the trade-off between lower accuracy physics and efficiency gains and lower memory requirements “good”? jeff@sep. stanford. edu

Project Objectives Extrapolation Work Flow • Answer two questions: – ABSOLUTE: Is one-way wavefield extrapolation accurate enough for waveform inversion? – RELATIVE: Is the trade-off between lower accuracy physics and efficiency gains and lower memory requirements “good”? jeff@sep. stanford. edu

Agenda • Review of waveform inversion • RWE forward modeling • 1 D Waveform inversion example jeff@sep. stanford. edu

Agenda • Review of waveform inversion • RWE forward modeling • 1 D Waveform inversion example jeff@sep. stanford. edu

Waveform Inversion • Goal: – Iteratively update velocity model in such a way that the mismatch between modeled and acquired transmission waveforms converges toward zero • Frequency domain approach (Pratt and Worthington, 1989) – Start with lowest frequency wavefield – Iteratively compute inverse problem solution until reach convergence – Repeat higher up sparsely sampled frequency spectrum jeff@sep. stanford. edu

Waveform Inversion • Goal: – Iteratively update velocity model in such a way that the mismatch between modeled and acquired transmission waveforms converges toward zero • Frequency domain approach (Pratt and Worthington, 1989) – Start with lowest frequency wavefield – Iteratively compute inverse problem solution until reach convergence – Repeat higher up sparsely sampled frequency spectrum jeff@sep. stanford. edu

Objective function • L 2 minimization of objective function jeff@sep. stanford. edu

Objective function • L 2 minimization of objective function • Compute negative gradient (greatest descent direction) • where - model parameters (non-linear) jeff@sep. stanford. edu

Gradient Calculation • Calculate gradient vector according to jeff@sep. stanford. edu
Mirrored half-space example jeff@sep. stanford. edu
Expected Ray-paths jeff@sep. stanford. edu
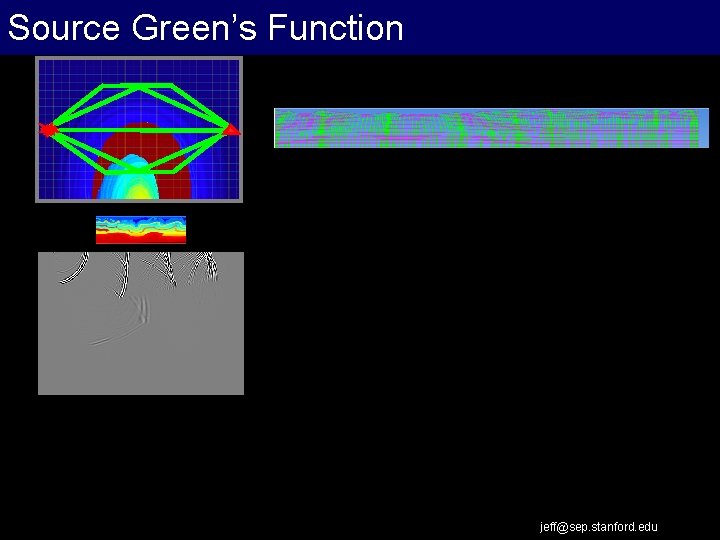
Source Green’s Function jeff@sep. stanford. edu
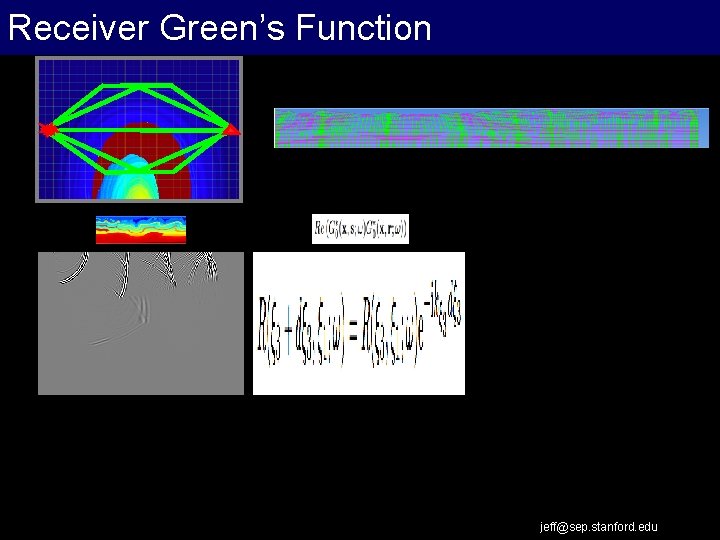
Receiver Green’s Function jeff@sep. stanford. edu
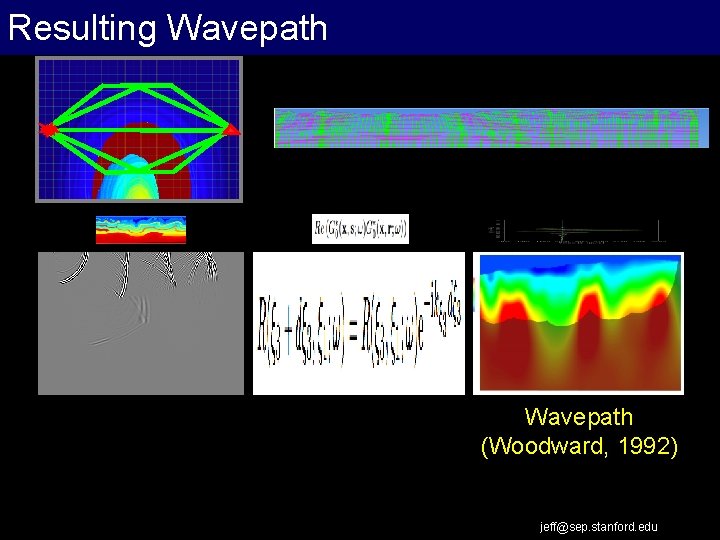
Resulting Wavepath (Woodward, 1992) jeff@sep. stanford. edu
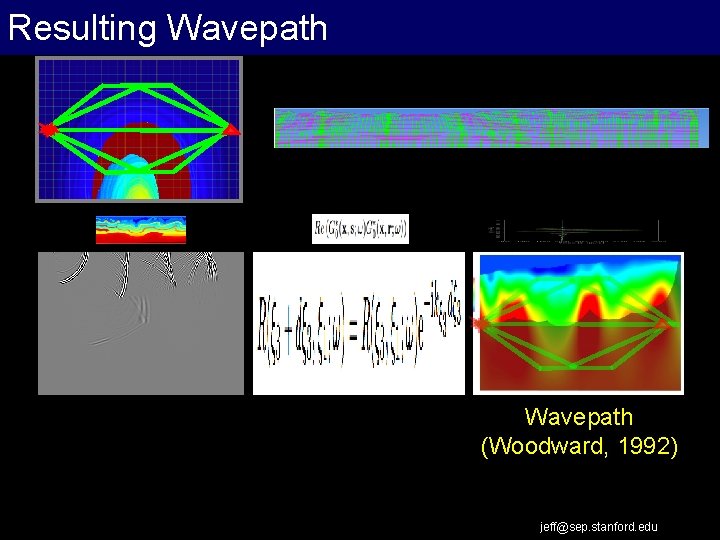
Resulting Wavepath (Woodward, 1992) jeff@sep. stanford. edu
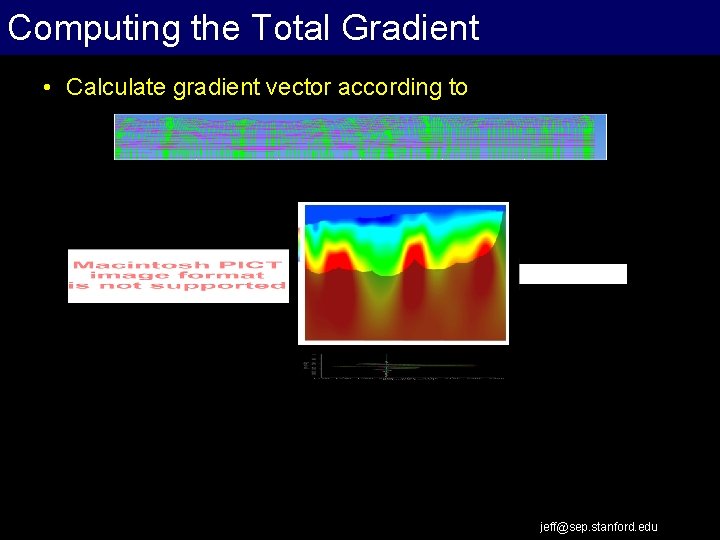
Computing the Total Gradient • Calculate gradient vector according to jeff@sep. stanford. edu

Agenda • Review of waveform inversion • RWE forward modeling • 1 D Waveform inversion example jeff@sep. stanford. edu

Turning-wave imaging Extrapolationcoordinate Work Flow • Wavefield extrapolation on mesh oriented in turning-wave propagation direction – Turning-waves propagate at low angle to extrapolation axis • Riemannian wavefield extrapolation (RWE) (Sava and Fomel, 2005) jeff@sep. stanford. edu

Example: SMAART JV Pluto 1. 5 jeff@sep. stanford. edu
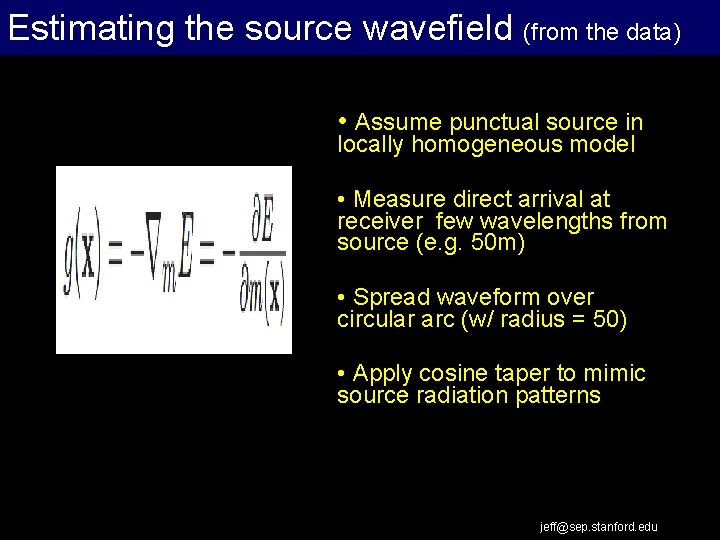
Estimating the source wavefield (from the data) • Assume punctual source in locally homogeneous model • Measure direct arrival at receiver few wavelengths from source (e. g. 50 m) • Spread waveform over circular arc (w/ radius = 50) • Apply cosine taper to mimic source radiation patterns jeff@sep. stanford. edu
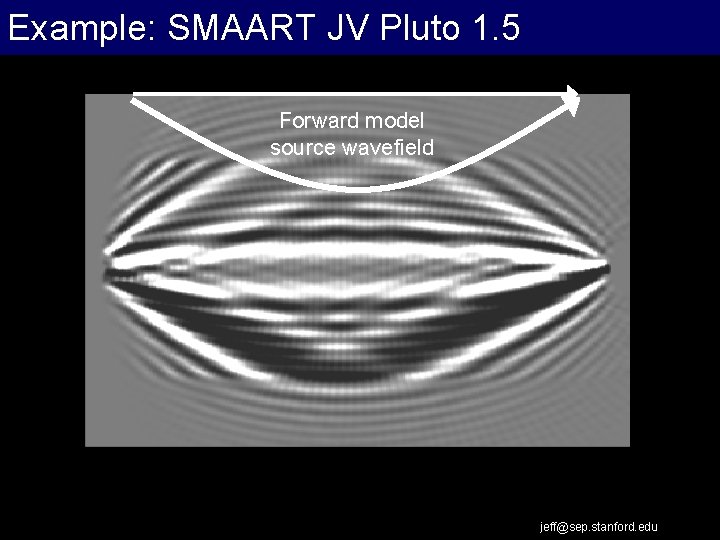
Example: SMAART JV Pluto 1. 5 Forward model source wavefield jeff@sep. stanford. edu
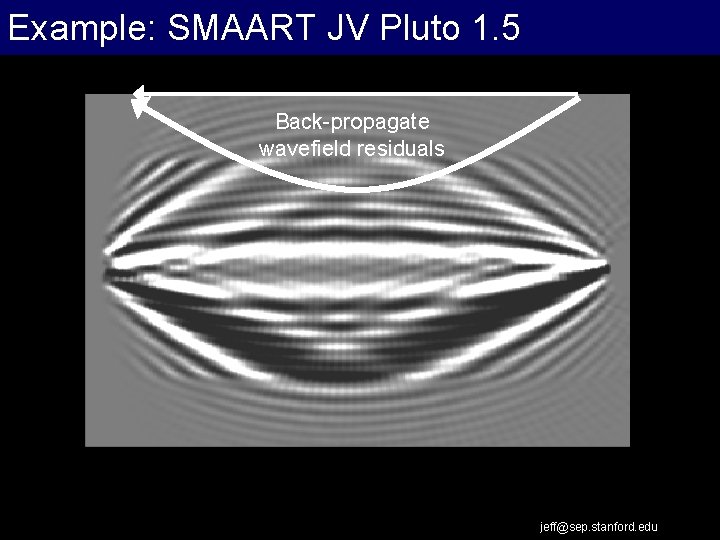
Example: SMAART JV Pluto 1. 5 Back-propagate wavefield residuals jeff@sep. stanford. edu
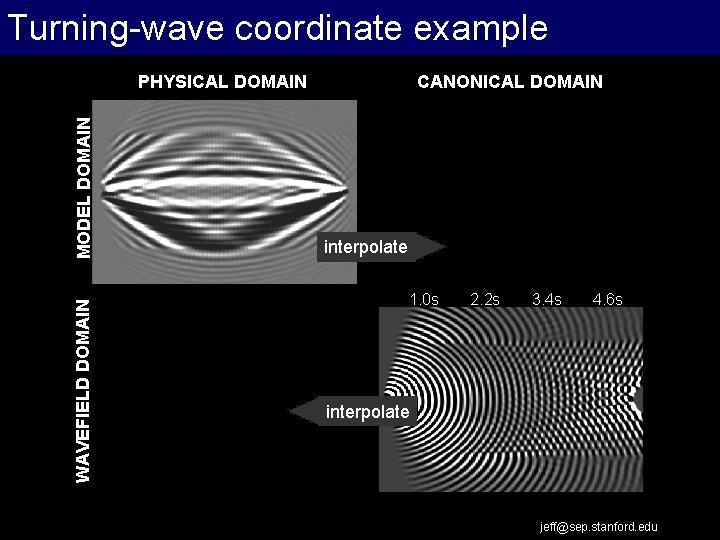
Turning-wave coordinate example WAVEFIELD DOMAIN MODEL DOMAIN PHYSICAL DOMAIN CANONICAL DOMAIN interpolate 1. 0 s 2. 2 s 3. 4 s 4. 6 s interpolate jeff@sep. stanford. edu
Wavefield Propagation Movie jeff@sep. stanford. edu
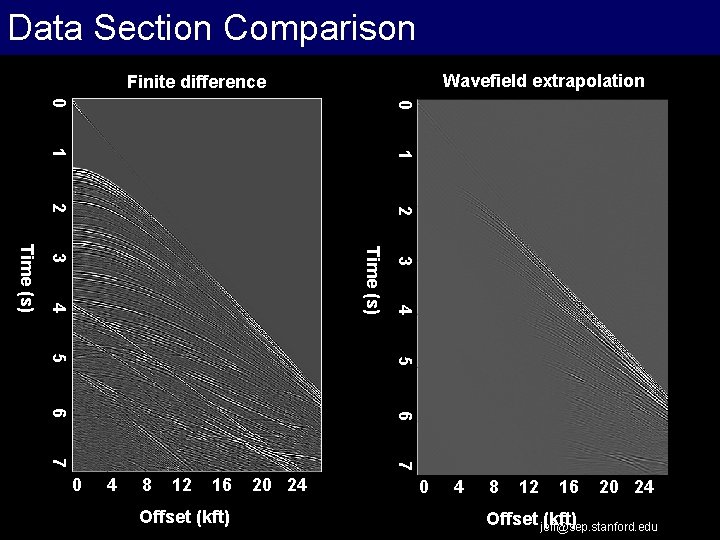
Data Section Comparison Wavefield extrapolation Finite difference 0 0 1 1 2 2 3 4 4 Time (s) 3 Time (s) 5 5 6 6 7 7 0 4 8 12 16 Offset (kft) 20 24 0 4 8 12 16 20 24 Offset jeff@sep. stanford. edu (kft)
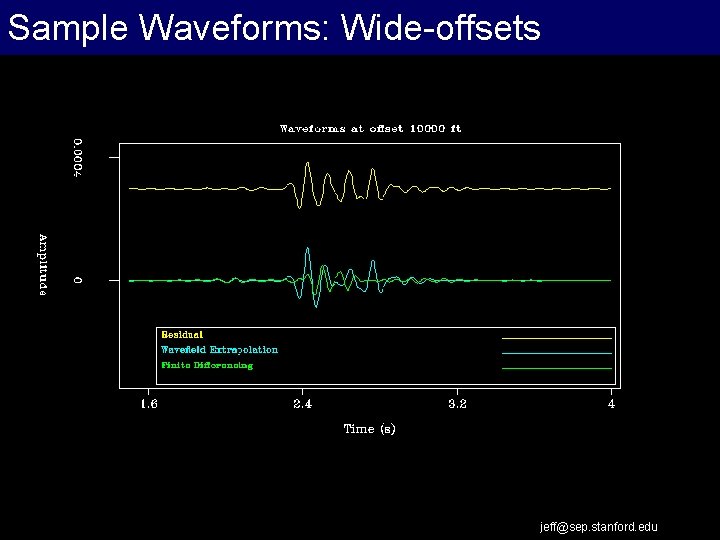
Sample Waveforms: Wide-offsets jeff@sep. stanford. edu
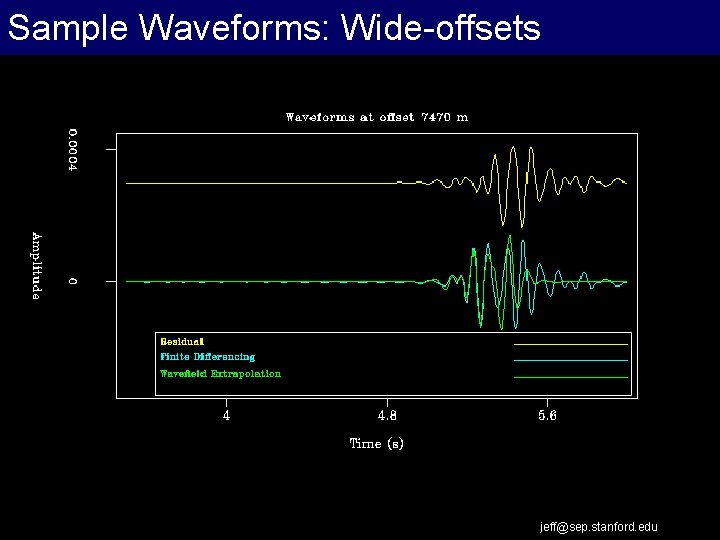
Sample Waveforms: Wide-offsets jeff@sep. stanford. edu

Sample Waveforms: Wide-offsets jeff@sep. stanford. edu
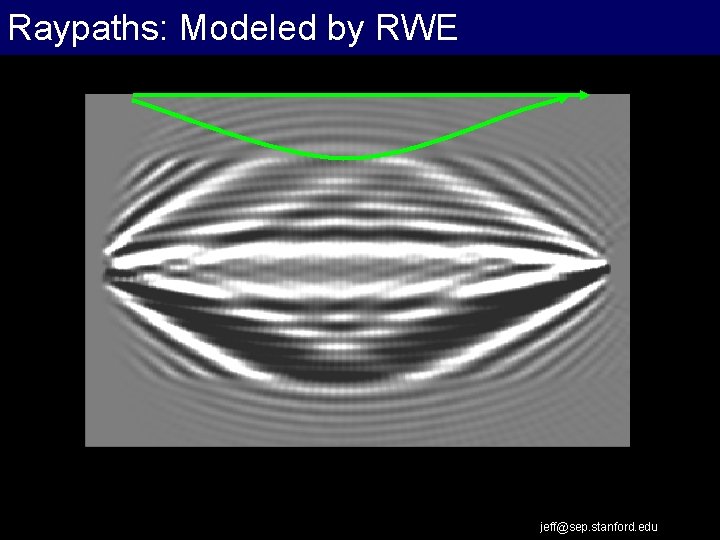
Raypaths: Modeled by RWE jeff@sep. stanford. edu
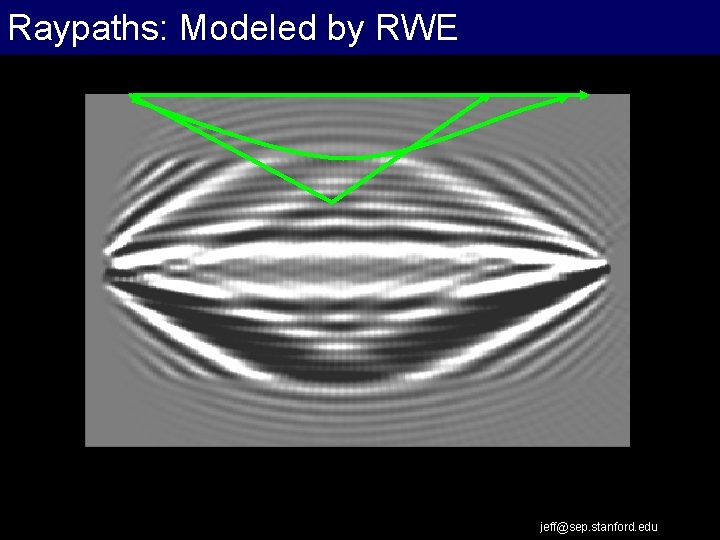
Raypaths: Modeled by RWE jeff@sep. stanford. edu
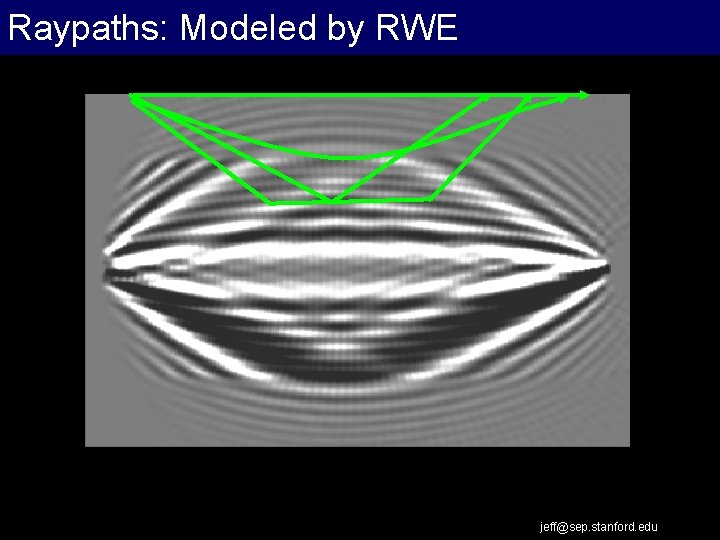
Raypaths: Modeled by RWE jeff@sep. stanford. edu
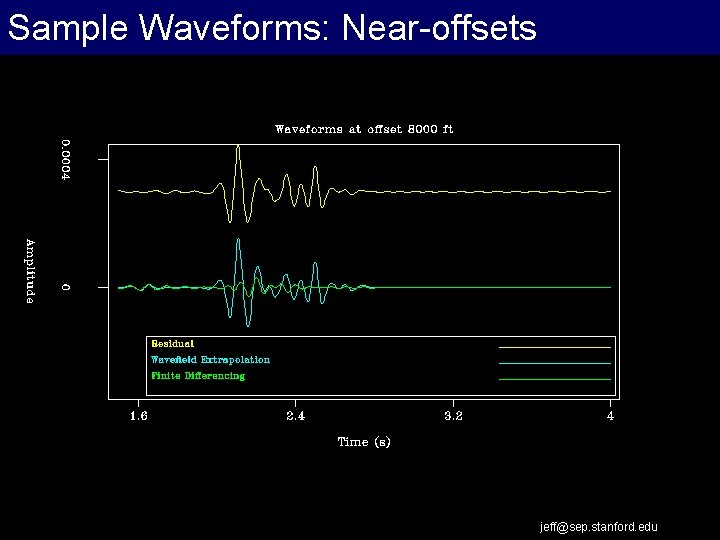
Sample Waveforms: Near-offsets jeff@sep. stanford. edu
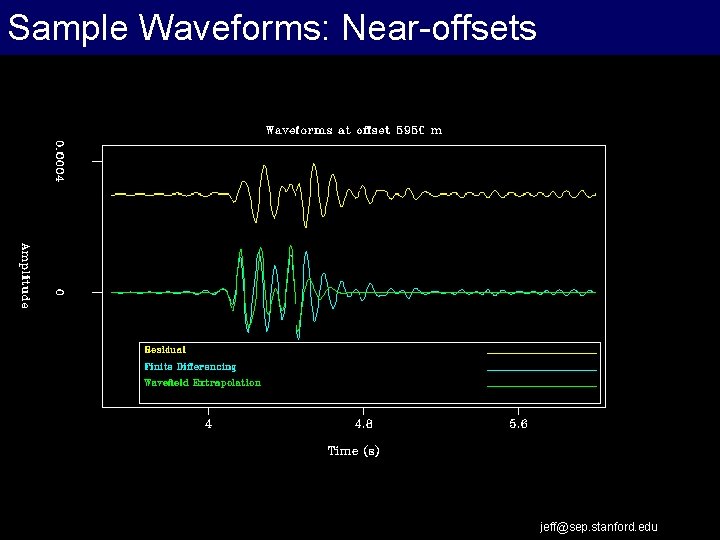
Sample Waveforms: Near-offsets jeff@sep. stanford. edu

Sample Waveforms: Near-offsets jeff@sep. stanford. edu

Raypaths: Not Modeled by RWE jeff@sep. stanford. edu
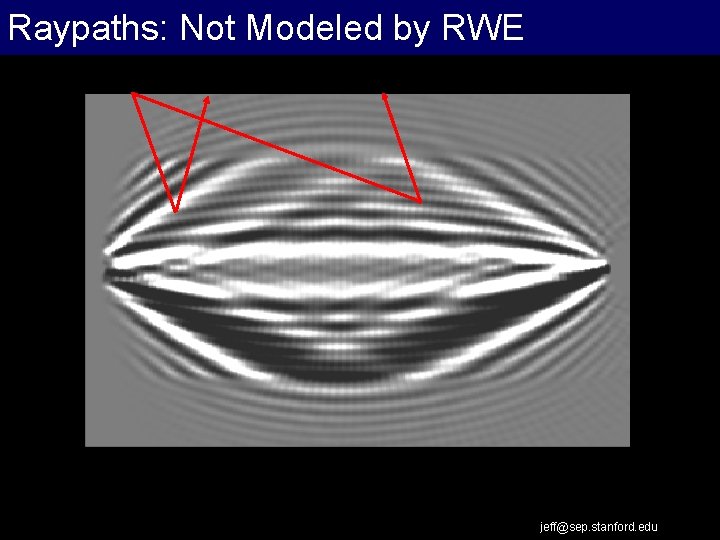
Raypaths: Not Modeled by RWE jeff@sep. stanford. edu
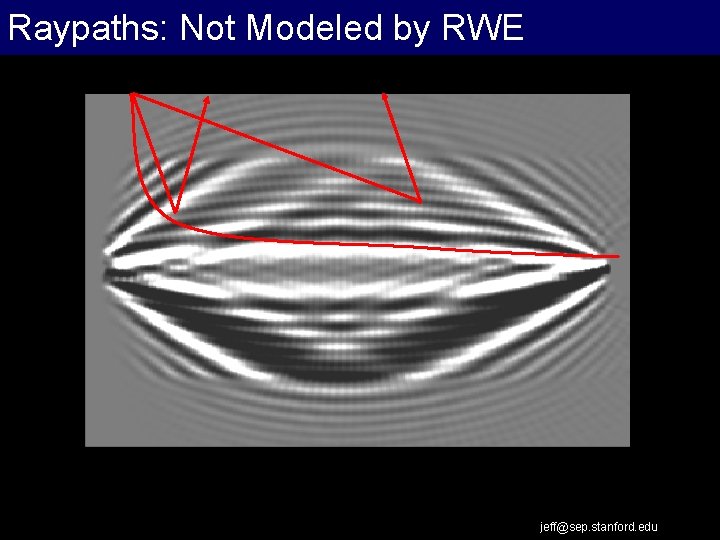
Raypaths: Not Modeled by RWE jeff@sep. stanford. edu

Agenda • Review of waveform inversion • RWE forward modeling • 1 D waveform inversion example jeff@sep. stanford. edu

1 -D Waveform Inversion Test • Velocity perturbation – 10% (+0. 2 km/s) – Depth: 1. 0 km – Width 0. 2 km • Inversion goal: – Recover velocity perturbation assuming v 0=2 km/s jeff@sep. stanford. edu
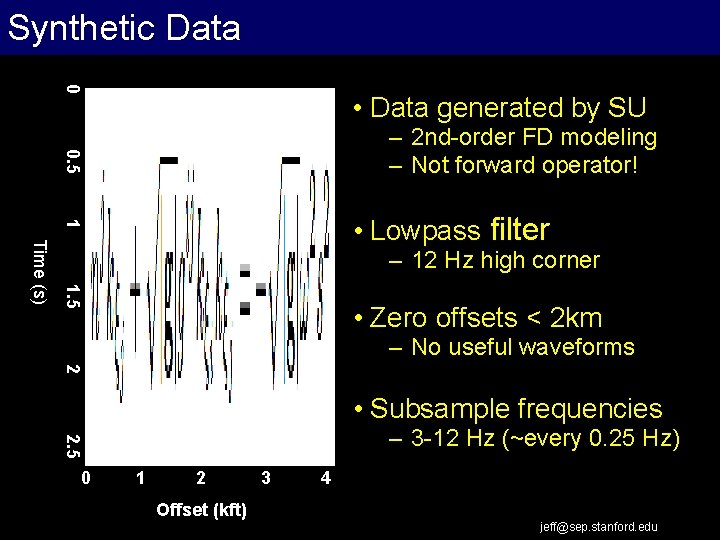
Synthetic Data 0 • Data generated by SU 0. 5 – 2 nd-order FD modeling – Not forward operator! 1 • Lowpass filter 1. 5 Time (s) – 12 Hz high corner • Zero offsets < 2 km – No useful waveforms 2 • Subsample frequencies 2. 5 – 3 -12 Hz (~every 0. 25 Hz) 0 1 2 3 4 Offset (kft) jeff@sep. stanford. edu

Inversion Results (5 non-linear iterations) Final Estimated Perturbation • Recovered perturbation – Nearly centered – About correct amplitude • Significant side-lobes – Missing low spatial frequencies • Similar result to 1 D test of Sirgue and Pratt (2005) jeff@sep. stanford. edu

Summary: • Alternate forward model for waveform inversion • One-way wavefield extrapolation (RWE) – “Turning-wave” mesh oriented in propagation direction • RWE and FD waveforms – match fairly well at wider offsets • 1 D Synthetic waveform inversion – Recovered 10% velocity perturbation jeff@sep. stanford. edu

Summary: Project Objectives Extrapolation Work Flow • Answer two questions: – ABSOLUTE: Is one-way wavefield extrapolation accurate enough for waveform inversion? • initial tests are positive • candidate for 3 D waveform inversion? • motivation for “true-amplitude” one-way operators – RELATIVE: Is the trade-off between lower accuracy physics and efficiency gains and lower memory requirements “good”? • too early to tell jeff@sep. stanford. edu

Acknowledgments • Schlumberger Cambridge Research • Drew Brenders • Colin Thomson • Clement Kostov jeff@sep. stanford. edu

Waveform inversion by one-way wavefield extrapolation Jeff Shragge SEP-125 pp 77 -100 jeff@sep. stanford. edu

Inversion Results (5 non-linear iterations) Cumulative Estimate • Recovered perturbation – Nearly centered – About correct amplitude • Significant side-lobes – Inadequately sampled frequency spectrum • Similar result to 1 D test of Sirgue and Pratt (2005) jeff@sep. stanford. edu

Geometric: Migration from Topography CANONICAL DOMAIN MODEL DOMAIN PHYSICAL DOMAIN IMAGE DOMAIN interpolate (Shragge and Sava, 2005)� jeff@sep. stanford. edu

RWE: Requirements Two requirements: i) Propagating wavefields in generalized coordinate systems RIEMANNIAN WAVEFIELD EXTRAPOLATION ii) Creating the specific topographic coordinate system MESH GENERATION jeff@sep. stanford. edu
Problem 1: (Semi)-orthogonality jeff@sep. stanford. edu

Problem 1: (Semi)-orthogonality jeff@sep. stanford. edu
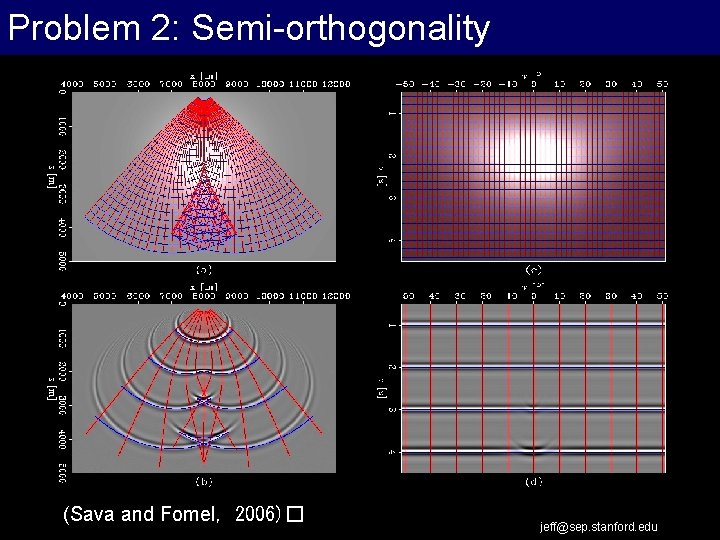
Problem 2: Semi-orthogonality (Sava and Fomel, 2006)� jeff@sep. stanford. edu
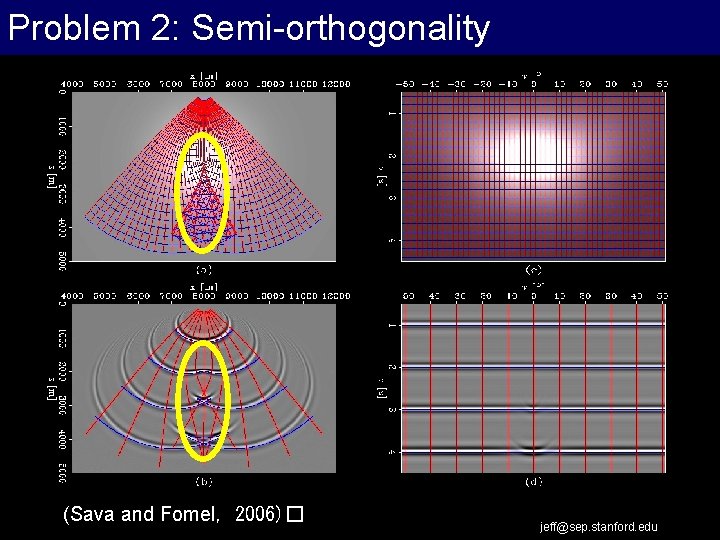
Problem 2: Semi-orthogonality (Sava and Fomel, 2006)� jeff@sep. stanford. edu

Proposed Solution • Generalize wavefield extrapolation to nonorthogonal coordinate systems • Concentrate on improving mesh design: – Well-formed meshes • e. g. non-triplicating, minimal clustering – Smoother coefficient fields • Smooth fields fewer reference parameter sets jeff@sep. stanford. edu

RWE: Helmholtz equation Coordinate system Laplacian (associated) metric tensor Sava and Fomel (2005) jeff@sep. stanford. edu
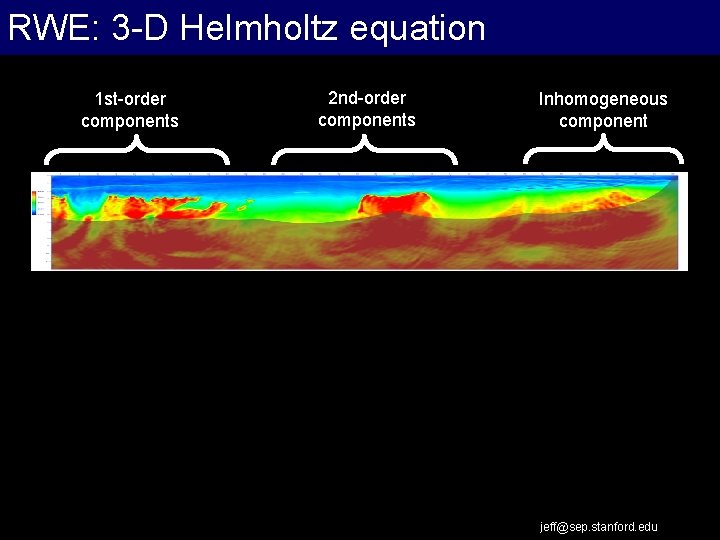
RWE: 3 -D Helmholtz equation 1 st-order components 2 nd-order components Inhomogeneous component jeff@sep. stanford. edu
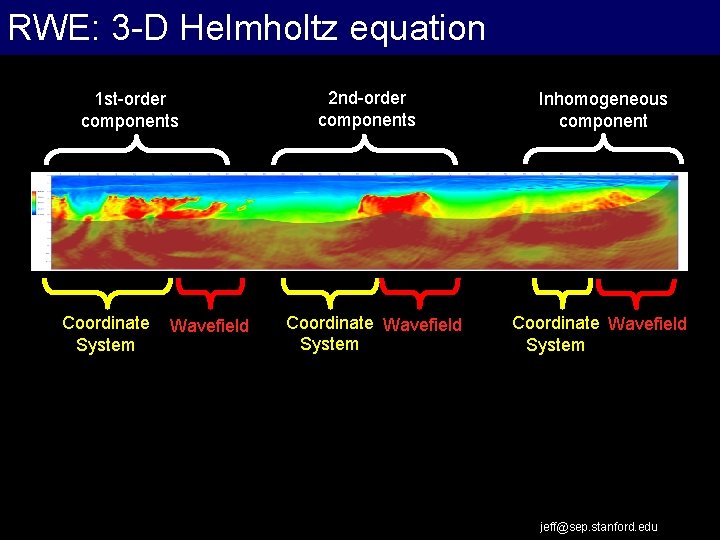
RWE: 3 -D Helmholtz equation 1 st-order components Coordinate System Wavefield 2 nd-order components Coordinate Wavefield System Inhomogeneous component Coordinate Wavefield System jeff@sep. stanford. edu
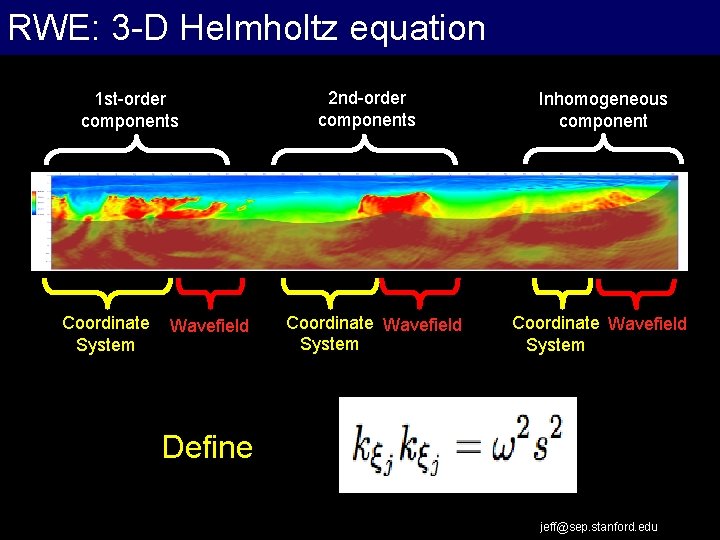
RWE: 3 -D Helmholtz equation 1 st-order components Coordinate System Wavefield 2 nd-order components Coordinate Wavefield System Inhomogeneous component Coordinate Wavefield System Define jeff@sep. stanford. edu
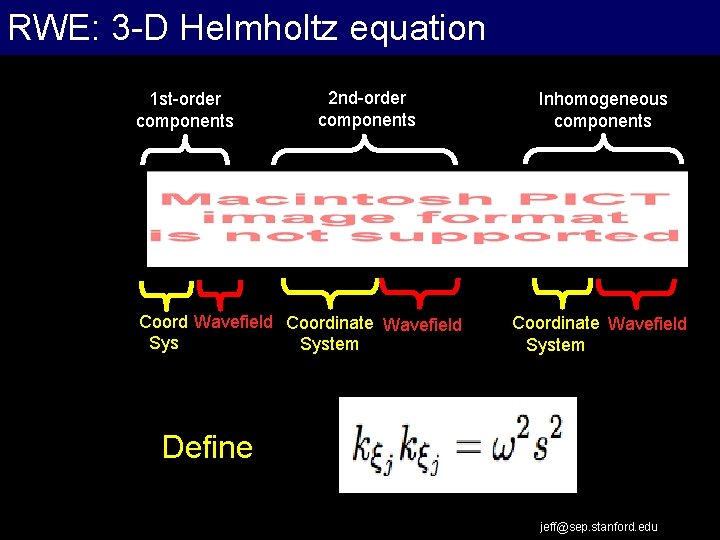
RWE: 3 -D Helmholtz equation 1 st-order components 2 nd-order components Coord Wavefield Coordinate Wavefield System Inhomogeneous components Coordinate Wavefield System Define jeff@sep. stanford. edu

RWE: Dispersion relation Define jeff@sep. stanford. edu

Cartesian Riemannian RWE: Dispersion relation nj =0, j = 1, 3 gij =1, i = j gij =0, i j jeff@sep. stanford. edu

RWE: 3 -D Extrapolation wavenumber • Define extrapolation direction – i. e. i=3 • “Complete the square” – isolate extrapolation wavenumber jeff@sep. stanford. edu

RWE: 3 -D Extrapolation wavenumber • Define extrapolation direction – i. e. i=3 • “Complete the square” – isolate extrapolation wavenumber jeff@sep. stanford. edu

RWE: 3 -D Extrapolation wavenumber • Further approximations reduce coefficient numbers – Kinematic, weak non-orthogonality • Need good characterization of vector fields – N-D Lloyd’s algorithm (Clapp, Tomorrow 8: 35 -8: 50) jeff@sep. stanford. edu

3 D RWE Summary - I Issue Fully orthogonal Semi-orthogonal Non-orthogonal # of coefficients 7 8 10 # of coefficients “kinematic” approx 4 5 7 coefficient smoothness smooth the velocity model smoother by design # reference coefficients more potential fewer jeff@sep. stanford. edu

3 D RWE Summary - II Issue Fully orthogonal Semi-orthogonal Non-orthogonal non-triplicating smooth the velocity model by design SSF + ? higher-order extrapolator SSF + FFD/PSC memory (4 -7)*nx*ny*nz (5 -8)*nx*ny*nz (7 -10)*nx*ny*nz SSF Kernal cost FFDs +1. x*SSF FFDs + 1. x*SSF jeff@sep. stanford. edu

Example: Green’s Function Extrapolation Work Flow Estimation CANONICAL DOMAIN WAVEFIELD DOMAIN MODEL DOMAIN PHYSICAL DOMAIN (Sava and Fomel, 2006)� interpolate jeff@sep. stanford. edu

Forward Model (Sirgue and Pratt, 2004) • Solutions to the acoustic Helmholtz equation • Compare calculated wavefield to observed data: – Generate monochromatic residual wavefield • Implement Born approximation implicitly – Strong velocity model errors cycle-skipping jeff@sep. stanford. edu
- Slides: 87