Waveform Design For Active Sensing Systems A Computational

Waveform Design For Active Sensing Systems – A Computational Approach 1

Outline • Introduction • Waveform design – Correlation § Single sequence § Sequence set § Correlation lower bound • Waveform design – Correlation & Doppler • Concluding remarks 2

Outline • Introduction • Waveform design – Correlation constraint § Single sequence § Sequence set § Correlation lower bound • Waveform design – Correlation & Doppler • Concluding remarks 3

Active Sensing System The goal is to determine properties of targets or propagation medium by transmitting waveforms and analyzing returned ones • Radar, Sonar, Medical imaging, Wireless Channel Estimation 4

Christian Hülsmeyer Telemobiloscope designed in 1904 Reginald Fessenden First acoustic communication and echo ranging experiment in 1914 5

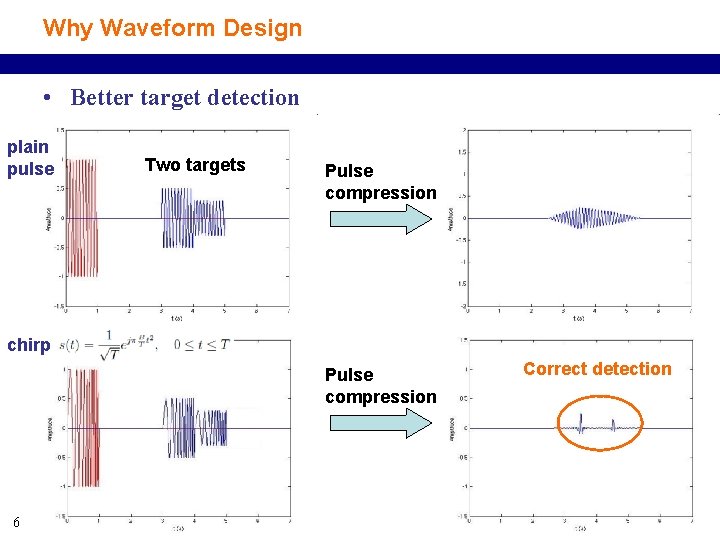
Why Waveform Design • Better target detection plain pulse Two targets Pulse compression chirp Pulse compression 6 Correct detection

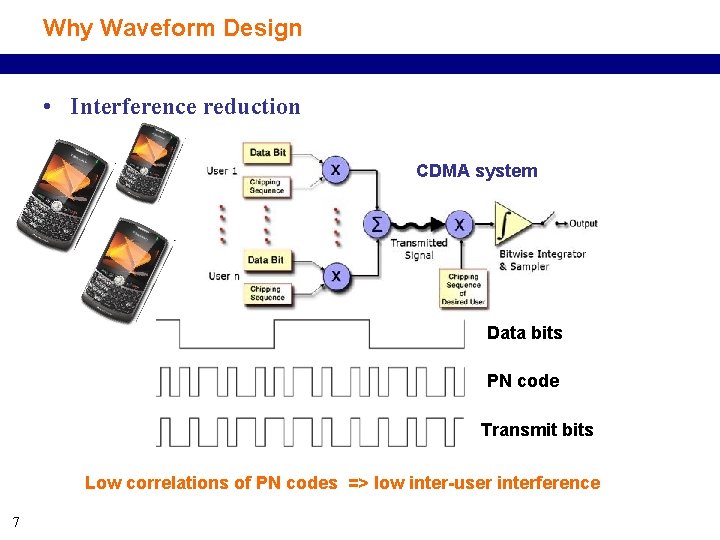
Why Waveform Design • Interference reduction CDMA system Data bits PN code Transmit bits Low correlations of PN codes => low inter-user interference 7

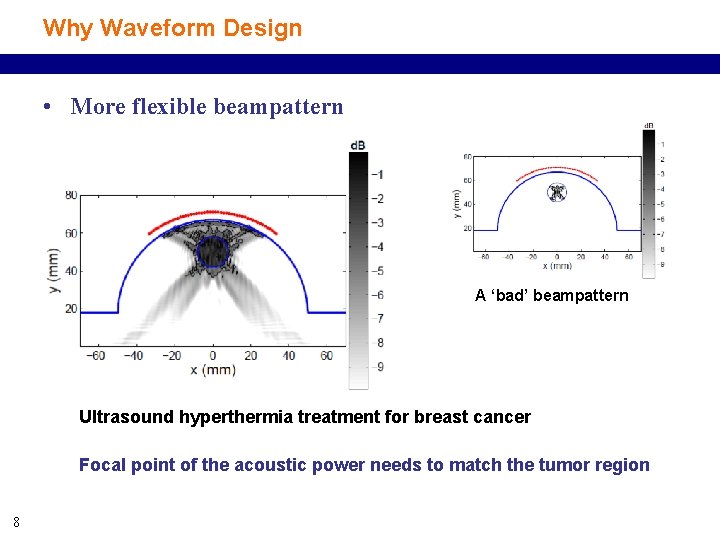
Why Waveform Design • More flexible beampattern A ‘bad’ beampattern Ultrasound hyperthermia treatment for breast cancer Focal point of the acoustic power needs to match the tumor region 8

Outline • Introduction • Waveform design – Correlation § Single sequence § Sequence set § Correlation lower bound • Waveform design – Correlation & Doppler • Concluding remarks 9

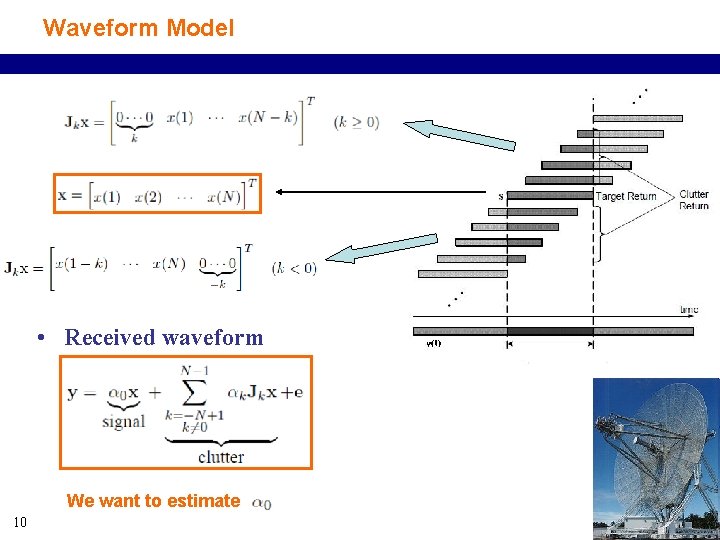
Waveform Model • Received waveform We want to estimate 10

Design Criterion • Matched filter estimate Auto-correlation of {x(n)} correlation sidelobes We aim to minimize correlation sidelobes to reduce interference Unit-modulus constraint 11

Existing Waveforms • Binary § Barker code Auto-correlation of Barker-7 Best binary code in terms of low correlation. But lengths <= 13 12

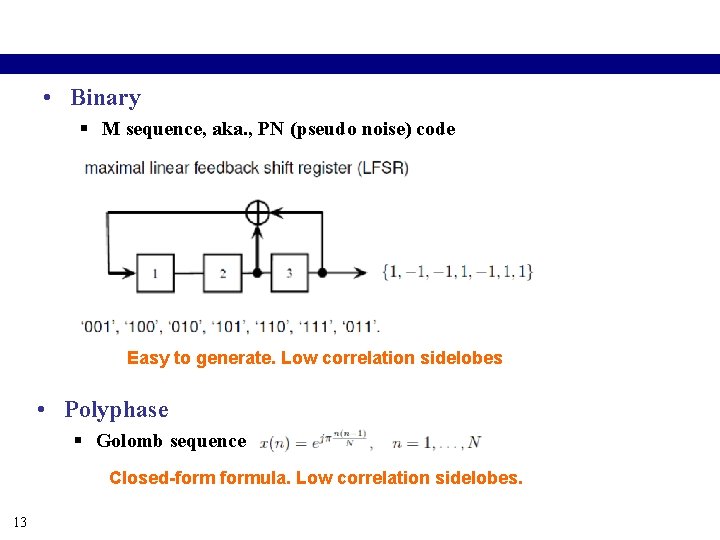
• Binary § M sequence, aka. , PN (pseudo noise) code Easy to generate. Low correlation sidelobes • Polyphase § Golomb sequence Closed-formula. Low correlation sidelobes. 13

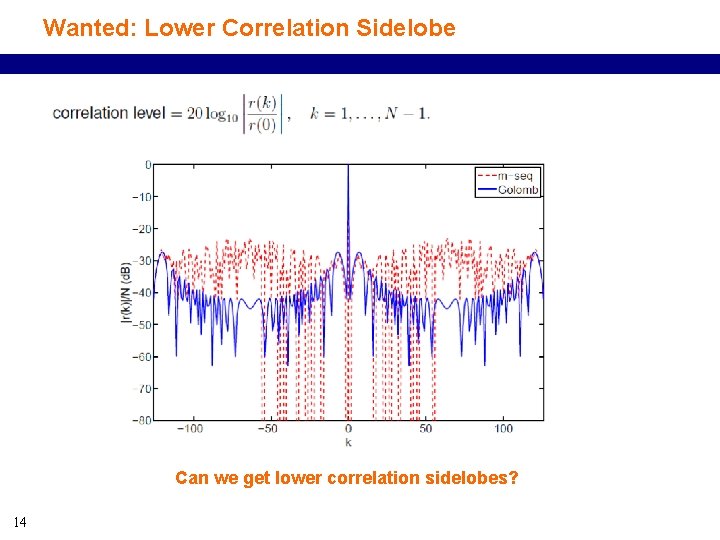
Wanted: Lower Correlation Sidelobe Can we get lower correlation sidelobes? 14

Unit-modulus Constraint • Arbitrary phases in [0, 2π] Q An AWG (arbitrary waveform generator), B&K Precision I More degrees of freedom => better control of correlation sidelobes We aim to develop computational algorithms, which generate unit-modular sequences with lower correlation sidelobes 15

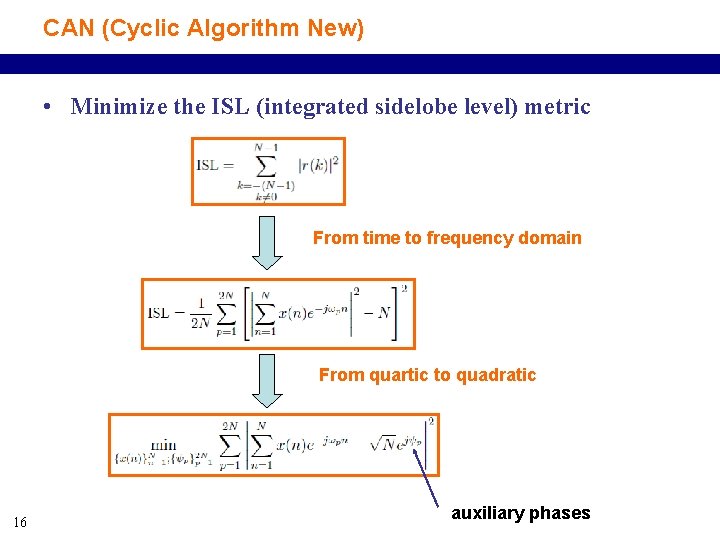
CAN (Cyclic Algorithm New) • Minimize the ISL (integrated sidelobe level) metric From time to frequency domain From quartic to quadratic 16 auxiliary phases

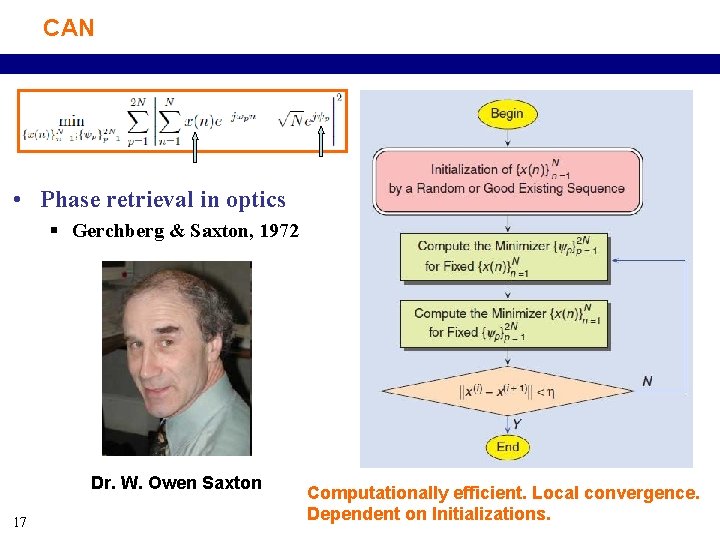
CAN • Phase retrieval in optics § Gerchberg & Saxton, 1972 Dr. W. Owen Saxton 17 Computationally efficient. Local convergence. Dependent on Initializations.

Example – Merit Factor • Random-phase sequence, M-sequence, Golomb vs. CAN(G) Merit Factor CAN gives the largest Merit Factor, i. e. , the smallest correlation sidelobes 18

Example – Correlation Level M-seq & Golomb Random-phase & CAN gives the lowest correlation sidelobes 19

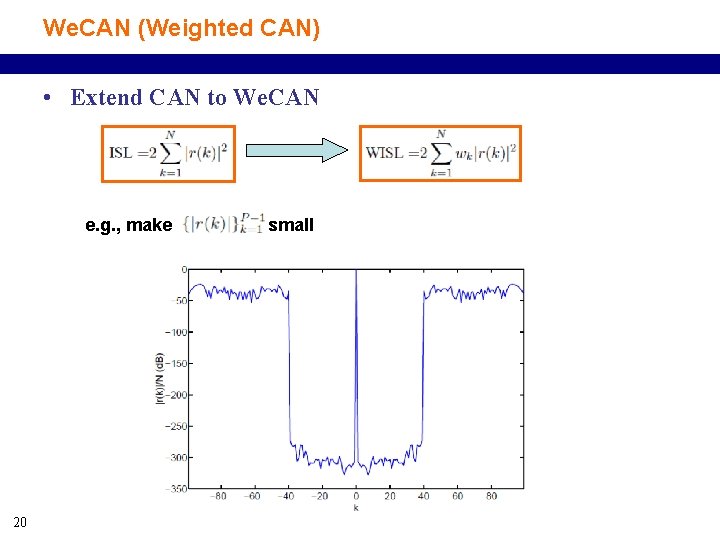
We. CAN (Weighted CAN) • Extend CAN to We. CAN e. g. , make 20 small

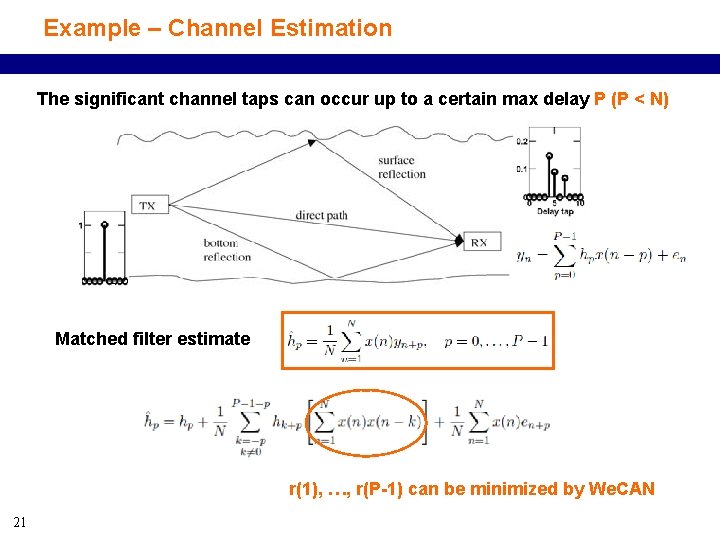
Example – Channel Estimation The significant channel taps can occur up to a certain max delay P (P < N) Matched filter estimate r(1), …, r(P-1) can be minimized by We. CAN 21

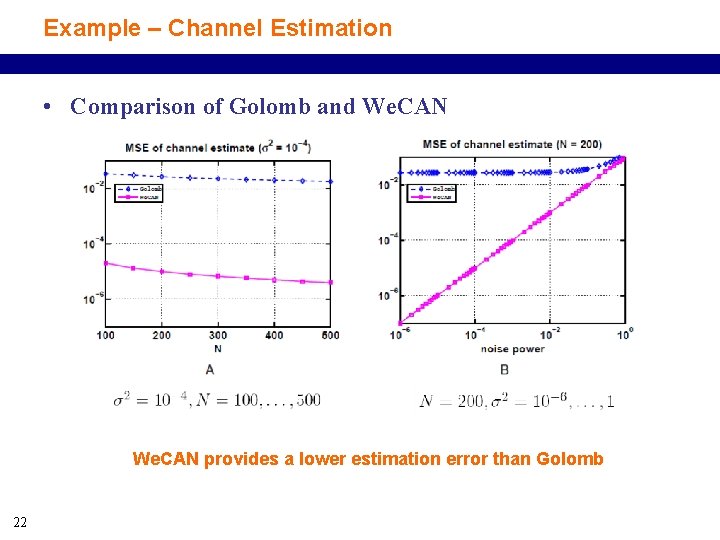
Example – Channel Estimation • Comparison of Golomb and We. CAN provides a lower estimation error than Golomb 22

Outline • Introduction • Waveform design – Correlation § Single sequence § Sequence set § Correlation lower bound • Waveform design – Correlation & Doppler • Concluding remarks 23

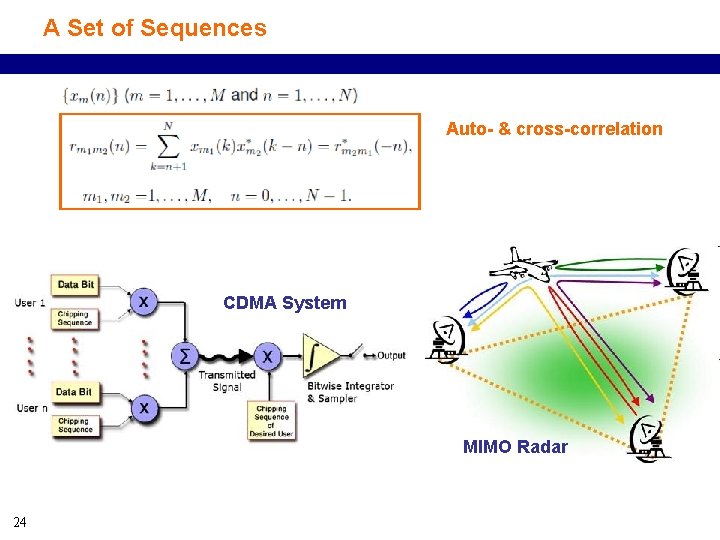
A Set of Sequences Auto- & cross-correlation CDMA System MIMO Radar 24

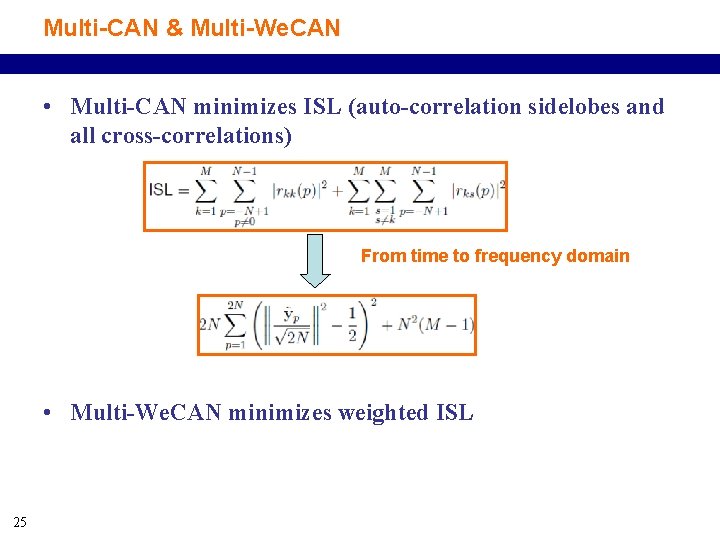
Multi-CAN & Multi-We. CAN • Multi-CAN minimizes ISL (auto-correlation sidelobes and all cross-correlations) From time to frequency domain • Multi-We. CAN minimizes weighted ISL 25

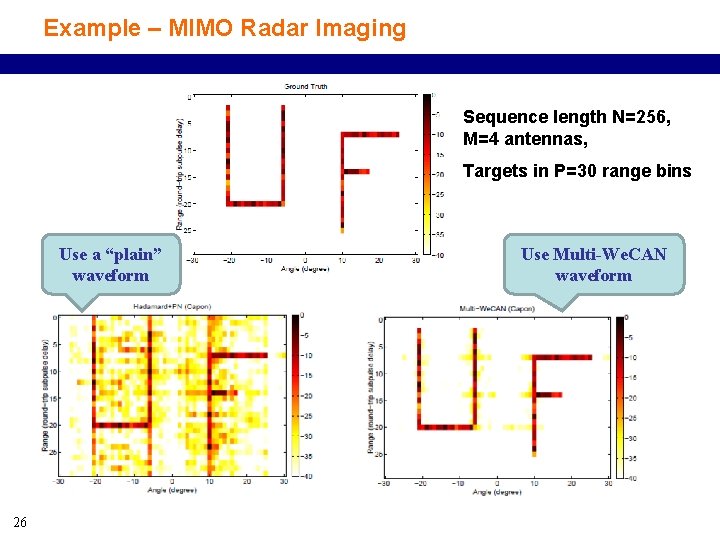
Example – MIMO Radar Imaging Sequence length N=256, M=4 antennas, Targets in P=30 range bins Use a “plain” waveform 26 Use Multi-We. CAN waveform

Outline • Introduction • Waveform design – Correlation § Single sequence § Sequence set § Correlation lower bound • Waveform design – Correlation & Doppler • Concluding remarks 27

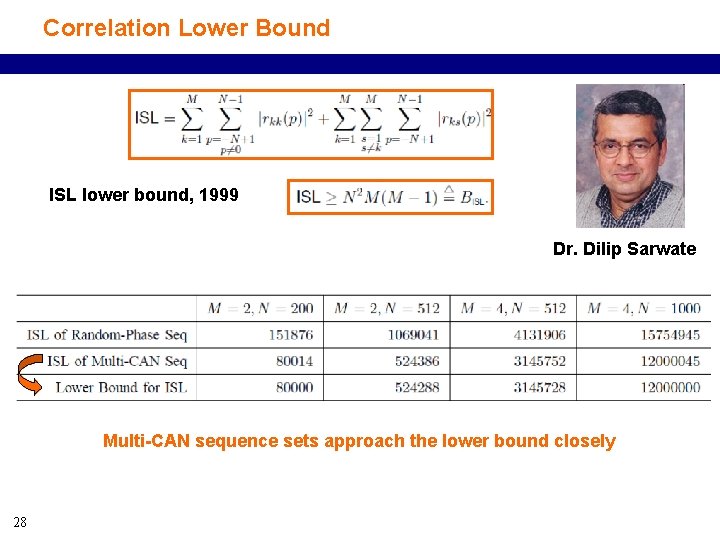
Correlation Lower Bound ISL lower bound, 1999 Dr. Dilip Sarwate Multi-CAN sequence sets approach the lower bound closely 28

Outline • Introduction • Waveform design – Correlation § Single sequence § Sequence set § Correlation lower bound • Waveform design – Correlation & Doppler • Concluding remarks 29

Correlation + Doppler effect • Ambiguity function (AF) Time delay & Doppler shifts AF is a two-dimensional extension of the auto-correlation function 30

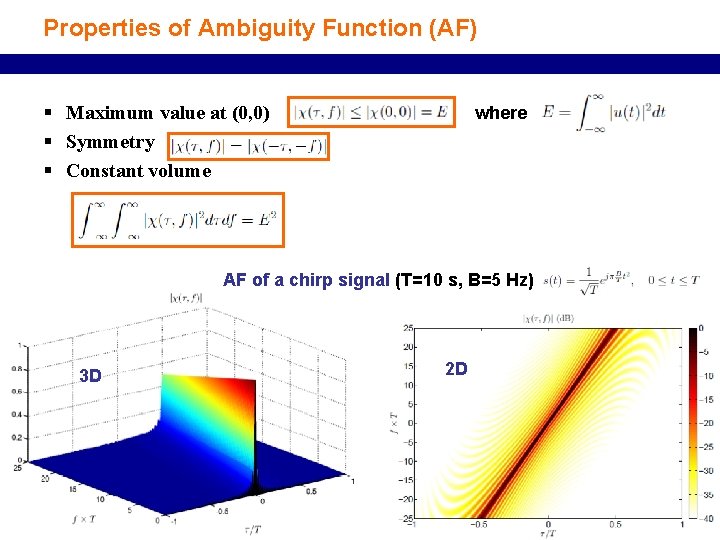
Properties of Ambiguity Function (AF) § Maximum value at (0, 0) § Symmetry § Constant volume where AF of a chirp signal (T=10 s, B=5 Hz) 3 D 31 2 D

Ambiguity Function (AF) • Desired AF shape § Doppler-tolerant (a high ridge) § Doppler-sensitive (thumbtack) “Probability and Information Theory, with Applications to Radar”, 1953 A heartfelt statement… Dr. Philip Woodward “The reader may feel some disappointment, not unshared by the writer, that the basic question of what to transmit remains substantially unanswered. ” But we can still analyze… 32

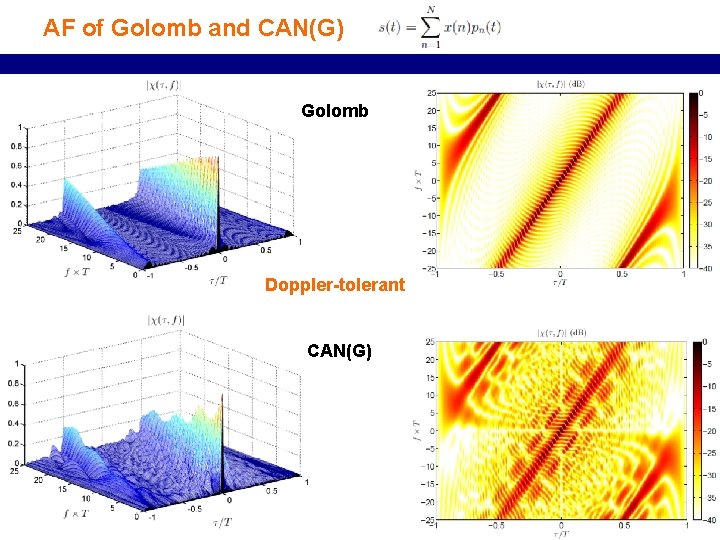
AF of Golomb and CAN(G) Golomb Doppler-tolerant CAN(G) 33

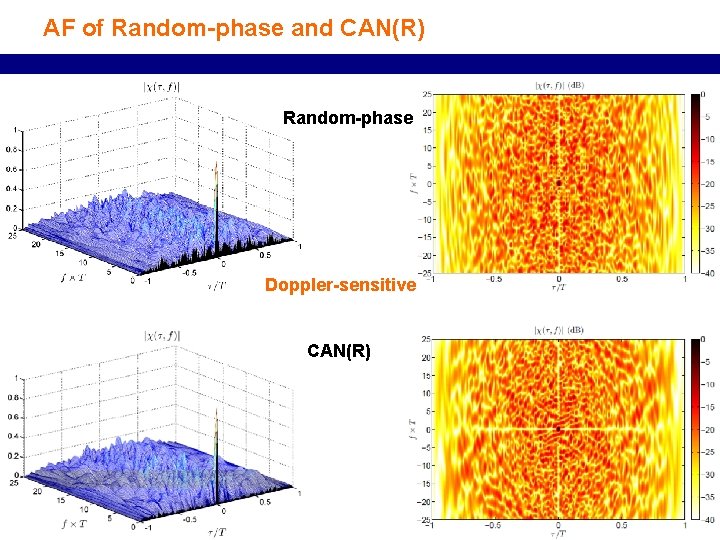
AF of Random-phase and CAN(R) Random-phase Doppler-sensitive CAN(R) 34

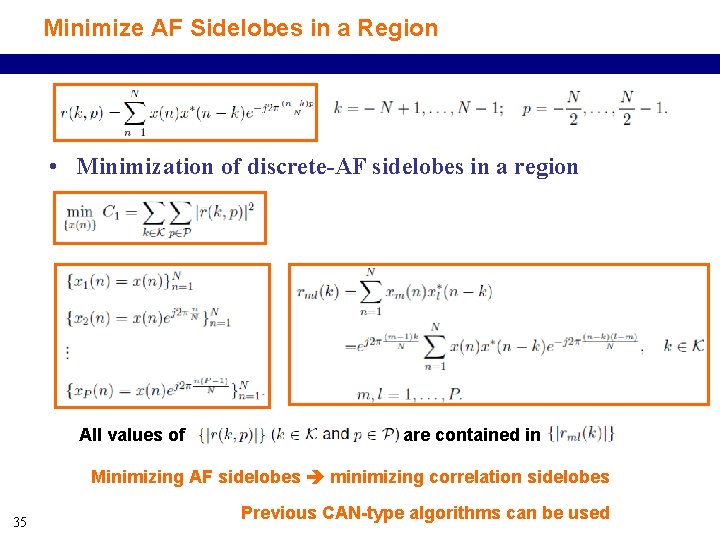
Minimize AF Sidelobes in a Region • Minimization of discrete-AF sidelobes in a region All values of are contained in Minimizing AF sidelobes minimizing correlation sidelobes 35 Previous CAN-type algorithms can be used

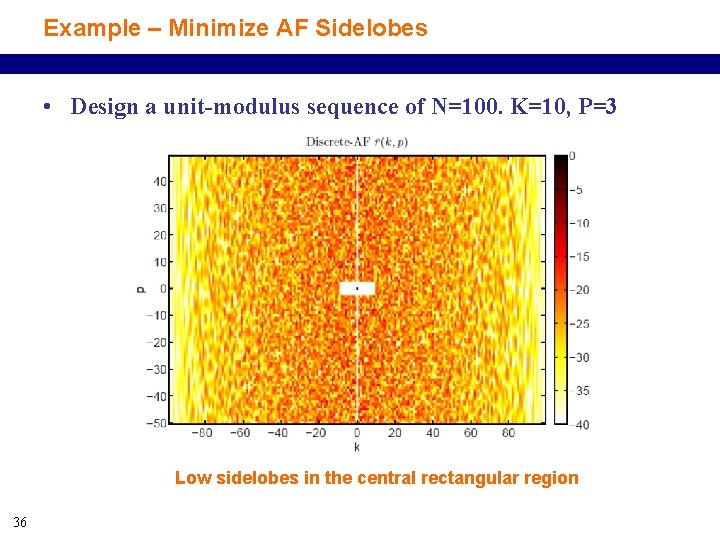
Example – Minimize AF Sidelobes • Design a unit-modulus sequence of N=100. K=10, P=3 Low sidelobes in the central rectangular region 36

Outline • Introduction • Waveform design – Correlation § Single sequence § Sequence set § Correlation lower bound • Waveform design – Correlation & Doppler • (Waveform design – other constraints) • Concluding remarks 37

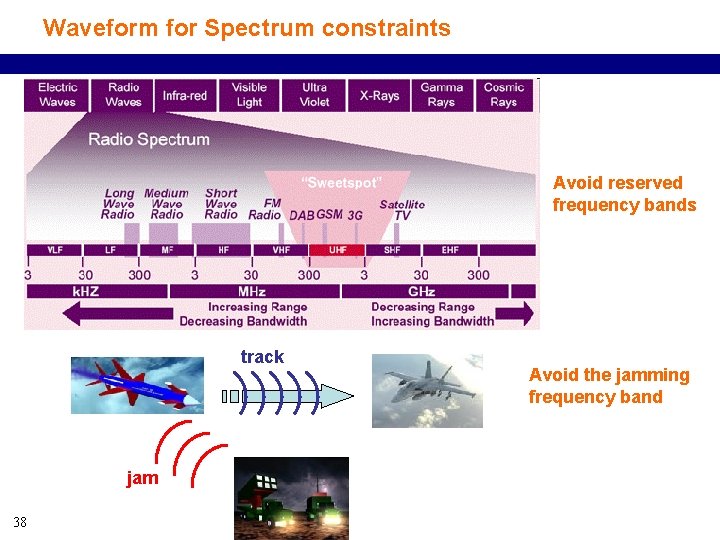
Waveform for Spectrum constraints Avoid reserved frequency bands track jam 38 Avoid the jamming frequency band

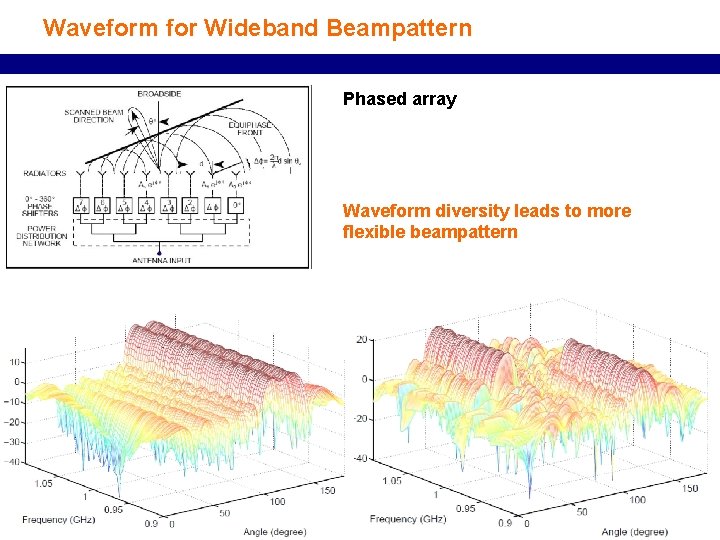
Waveform for Wideband Beampattern Phased array Waveform diversity leads to more flexible beampattern 39

Outline • Introduction • Waveform design – Correlation § Single sequence § Sequence set § Correlation lower bound • Waveform design – Correlation & Doppler • Concluding remarks 40

Concluding Remarks • Importance of waveform design for active sensing § Range compression, CDMA, channel estimation, beampattern • New computational algorithms of waveform design § Correlation, correlation + Doppler, correlation + spectrum § Unit-modulus (arbitrary phases => more degrees of freedom) § Better performance than existing waveforms 41

Thanks much 42