Wave superposition interference and reflection 1 Adding waves

Wave superposition, interference, and reflection 1

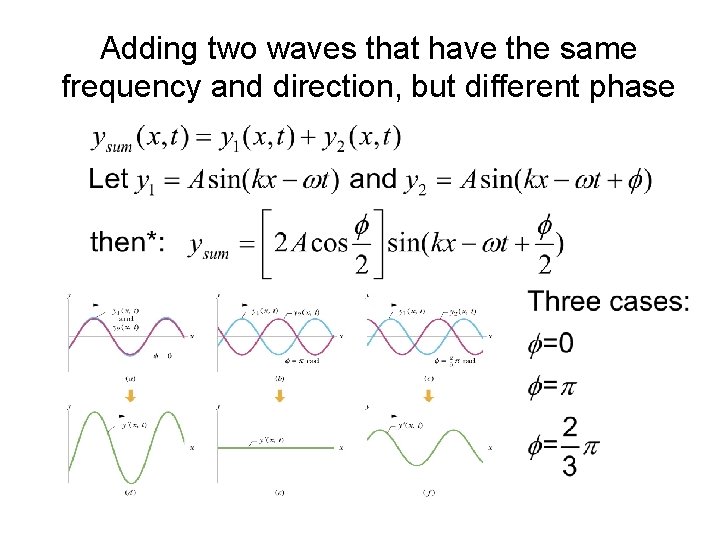
Adding waves: superposition When two waves are incident on the same place at the same time, their amplitudes can usually just be added. In the next few slides we will look at some special cases: (both with two waves at the same frequency and with the same amplitude) – same frequency and amplitude » superposition at a point in space » same direction, but different phase » opposite directions 2

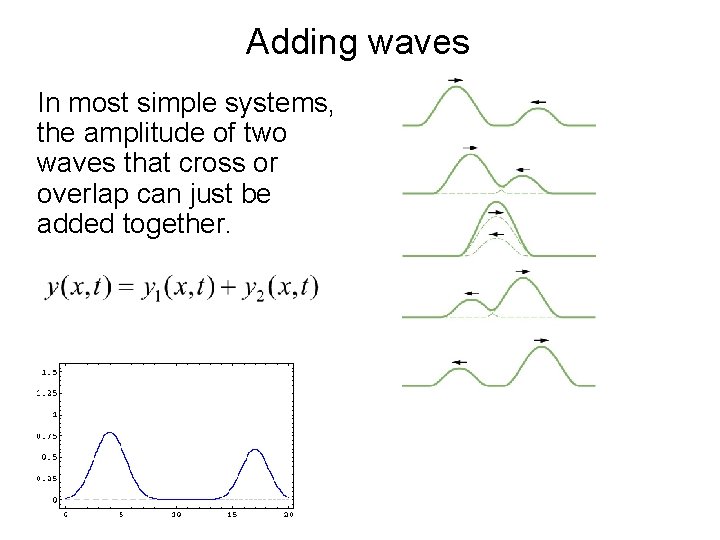
Adding waves In most simple systems, the amplitude of two waves that cross or overlap can just be added together. 3

Adding two equal amplitude waves at a point 4

For which phase difference is the superposition amplitude a maximum? a) =0 b) = /2 c) = 5

For which phase difference is the superposition amplitude a minimum? a) =0 b) = /2 c) = 6

Adding two waves that have the same frequency and direction, but different phase • What happens when the phase difference is 0? • What happens when the phase difference is /2? • What happens when the phase difference is ? 7

Constructive interference when =0. Destructive interference when =. Link to animation of two sine waves adding in and out of phase (Kettering) 8

What happens when a wave is incident on an immovable object? It reflects, travelling in the opposite direction and upside down. (Now watch patiently while your instructor plays with the demonstration. ) 9

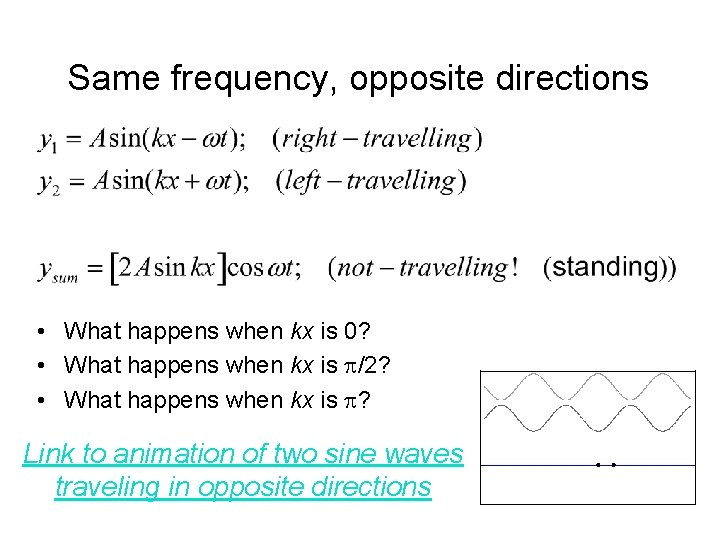
Same frequency, opposite directions • What happens when kx is 0? • What happens when kx is /2? • What happens when kx is ? Link to animation of two sine waves traveling in opposite directions 10

Standing waves Interfering waves traveling in opposite directions can produce fixed points called nodes. y 1 = ym sin(kx – wt) v=w/k y 2 = ym sin(kx + wt) y. T = y 1 + y 2 = 2 ym cos(wt) sin(kx) y. T=0 when kx = 0, p, 2 p. . . y. T(t)=maximum when kx = p/2, 3 p/2, 5 p/2. . . 11

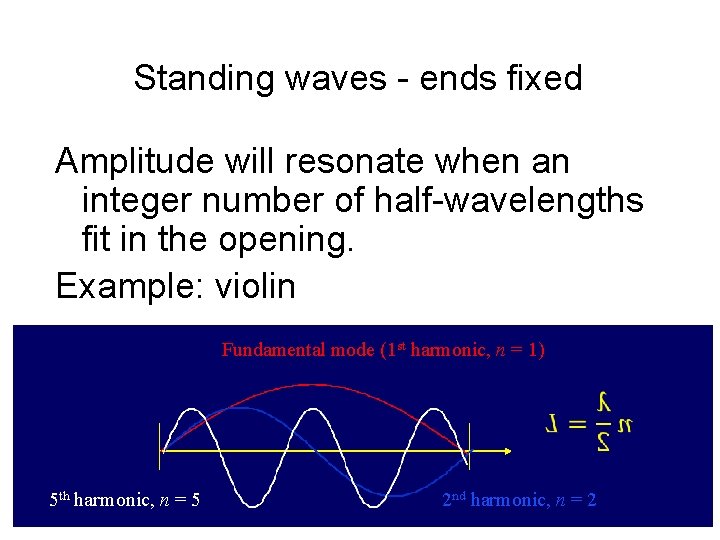
Standing waves - ends fixed Amplitude will resonate when an integer number of half-wavelengths fit in the opening. Example: violin Fundamental mode (1 st harmonic, n = 1) 5 th harmonic, n = 5 2 nd harmonic, n = 2 12

Both Ends Fixed 13

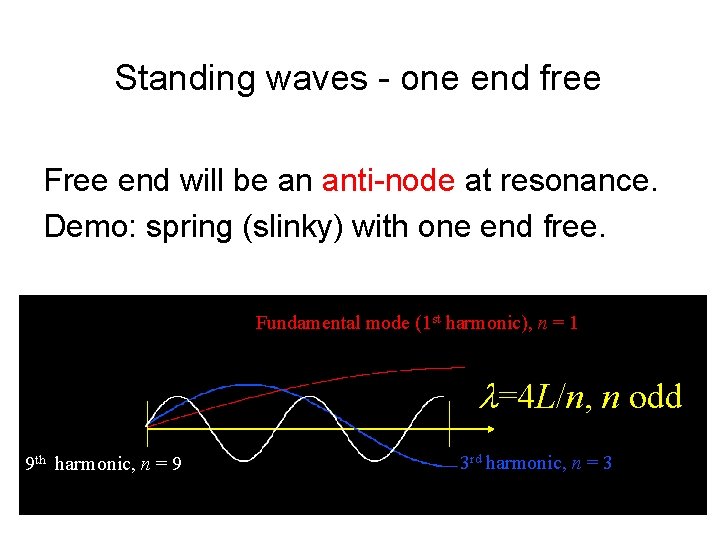
Standing waves - one end free Free end will be an anti-node at resonance. Demo: spring (slinky) with one end free. Fundamental mode (1 st harmonic), n = 1 l=4 L/n, n odd 9 th harmonic, n = 9 3 rd harmonic, n = 3 14

One End Open (e. g. Organ Pipe) 15

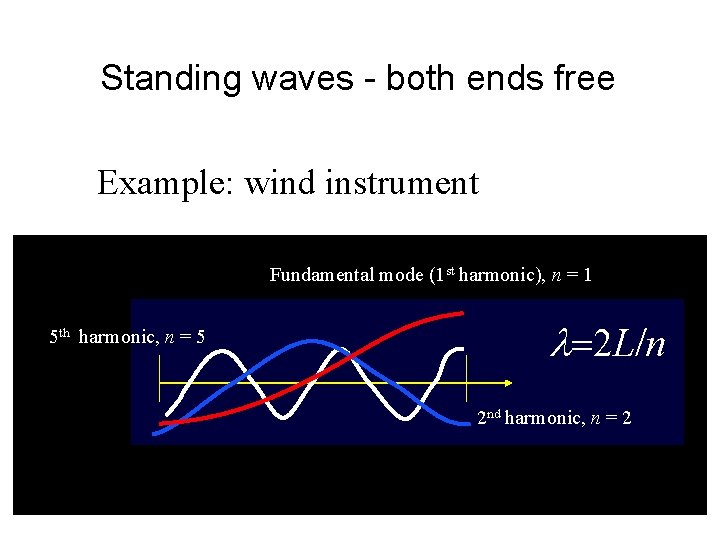
Standing waves - both ends free Example: wind instrument Fundamental mode (1 st harmonic), n = 1 5 th harmonic, n = 5 l=2 L/n 2 nd harmonic, n = 2 16

Both Ends Open (e. g. Organ Pipe) 17