Wave Properties of Light Sound Waves In General

Wave Properties of Light & Sound

Waves In General • Waves are a propagation of energy through a medium (material) • Waves depend on elasticity of the material – A wave passing through the medium applies an alternating unbalanced force to each molecule causing it to vibrate around its equilibrium or “rest” position.

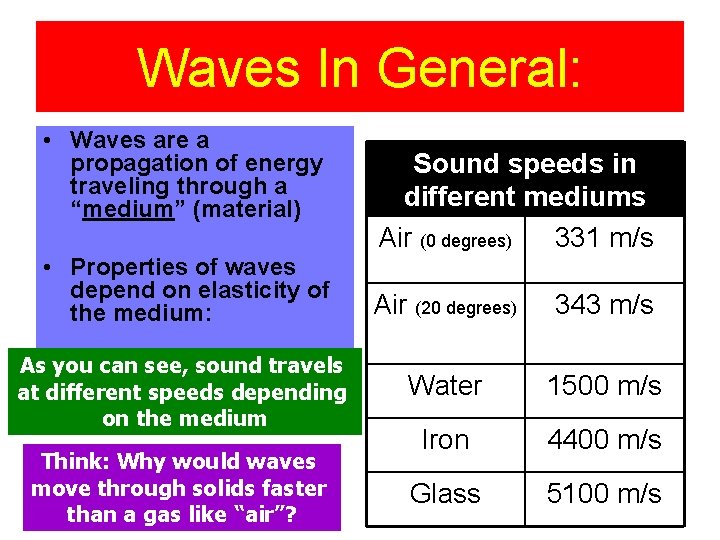
Waves In General: • Waves are a propagation of energy traveling through a “medium” (material) • Properties of waves depend on elasticity of the medium: Sound speeds in different mediums Air (0 degrees) 331 m/s Air (20 degrees) 343 m/s As you can see, sound travels at different speeds depending on the medium Water 1500 m/s Think: Why would waves move through solids faster than a gas like “air”? Iron 4400 m/s Glass 5100 m/s

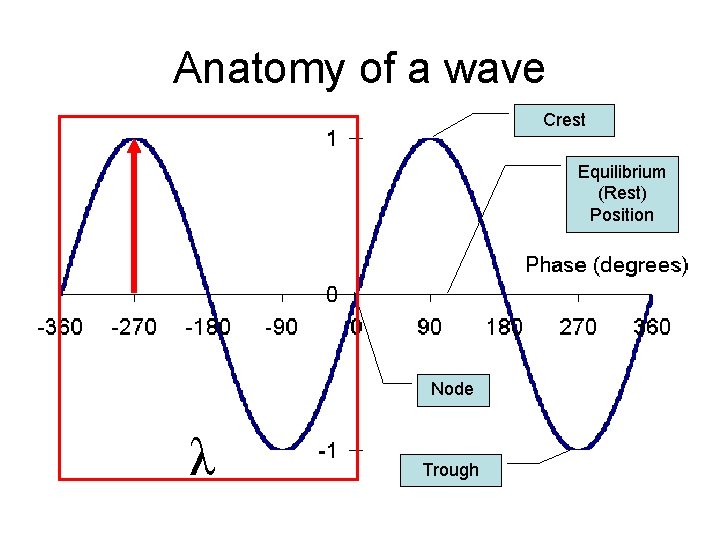
Anatomy of a wave Crest Equilibrium (Rest) Position Node λ Trough

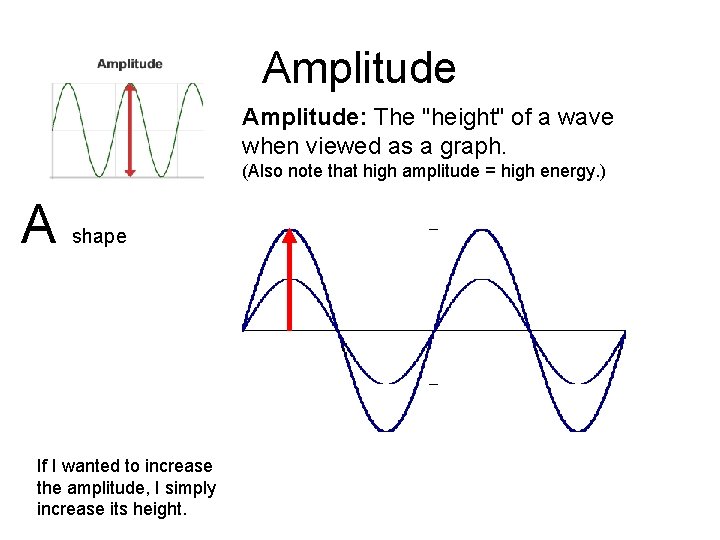
Amplitude: The "height" of a wave when viewed as a graph. (Also note that high amplitude = high energy. ) A shape If I wanted to increase the amplitude, I simply increase its height.

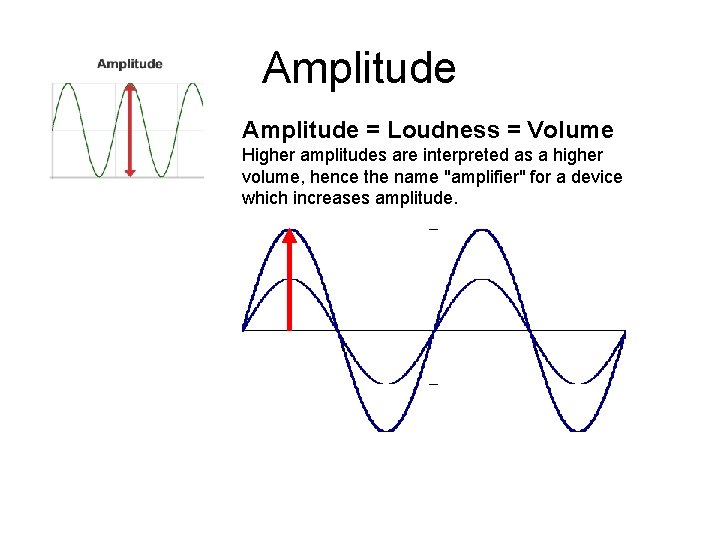
Amplitude = Loudness = Volume Higher amplitudes are interpreted as a higher volume, hence the name "amplifier" for a device which increases amplitude.

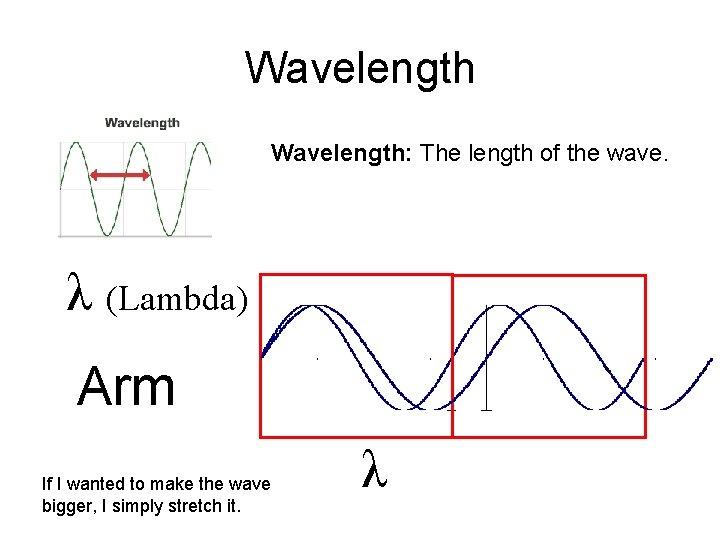
Wavelength: The length of the wave. λ (Lambda) Arm If I wanted to make the wave bigger, I simply stretch it. λ

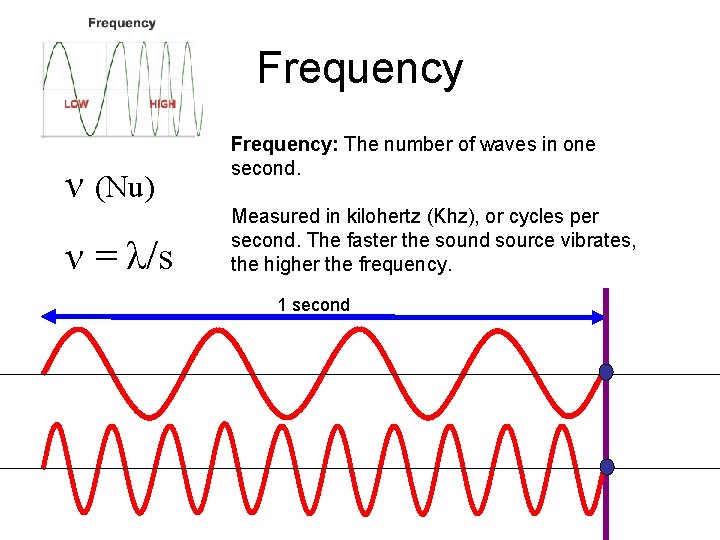
Frequency ν (Nu) ν = λ/s Frequency: The number of waves in one second. Measured in kilohertz (Khz), or cycles per second. The faster the sound source vibrates, the higher the frequency. 1 second

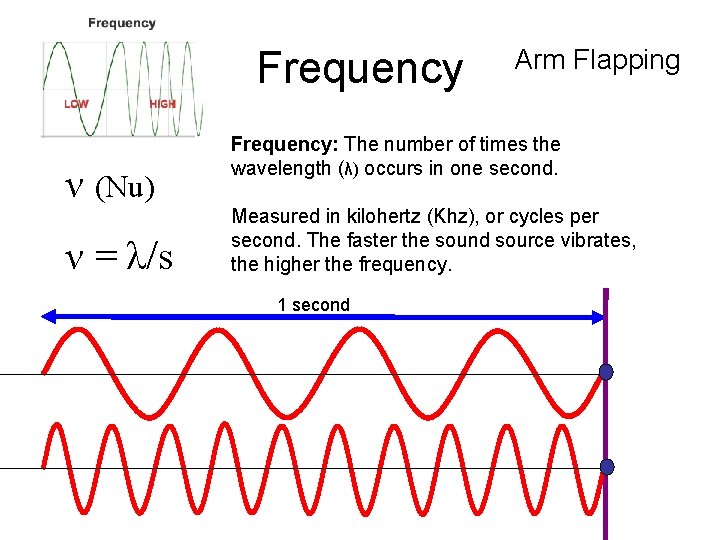
Frequency ν (Nu) ν = λ/s Arm Flapping Frequency: The number of times the wavelength (λ) occurs in one second. Measured in kilohertz (Khz), or cycles per second. The faster the sound source vibrates, the higher the frequency. 1 second

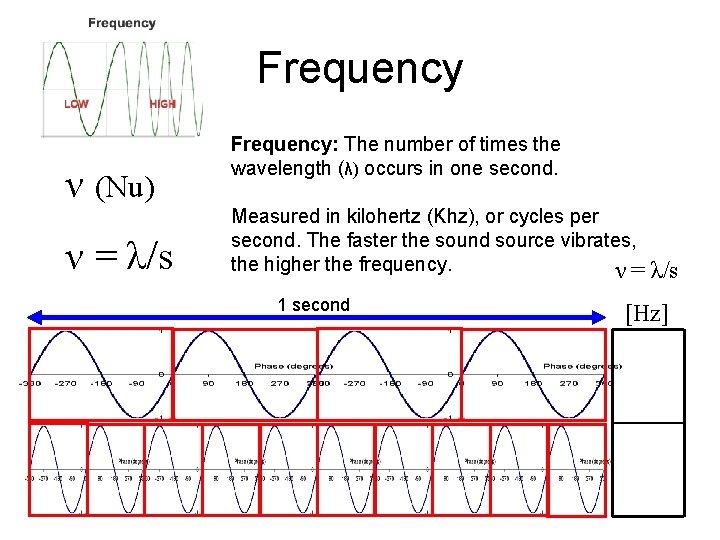
Frequency ν (Nu) ν = λ/s Frequency: The number of times the wavelength (λ) occurs in one second. Measured in kilohertz (Khz), or cycles per second. The faster the sound source vibrates, the higher the frequency. ν= 1 second λ/s [Hz]

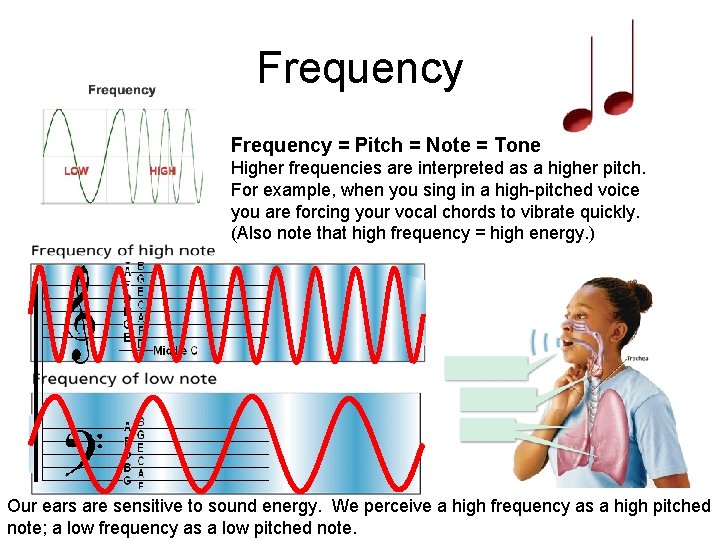
Frequency = Pitch = Note = Tone Higher frequencies are interpreted as a higher pitch. For example, when you sing in a high-pitched voice you are forcing your vocal chords to vibrate quickly. (Also note that high frequency = high energy. ) Our ears are sensitive to sound energy. We perceive a high frequency as a high pitched note; a low frequency as a low pitched note.

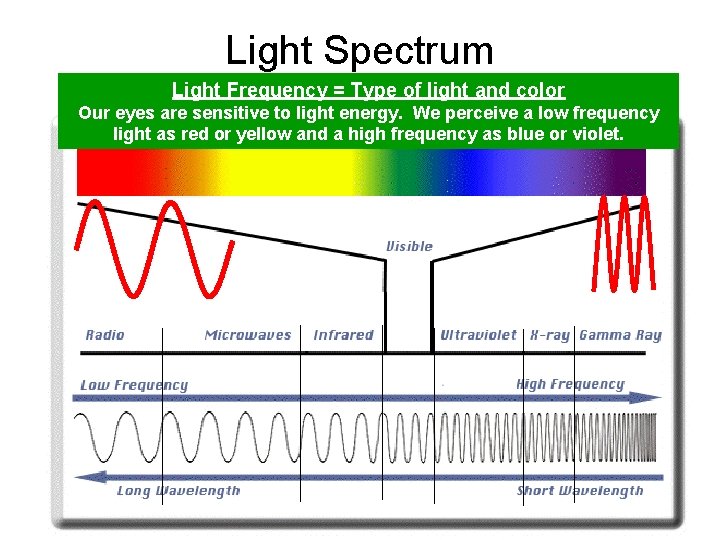
Light Spectrum Light Frequency = Type of light and color Our eyes are sensitive to light energy. We perceive a low frequency light as red or yellow and a high frequency as blue or violet.

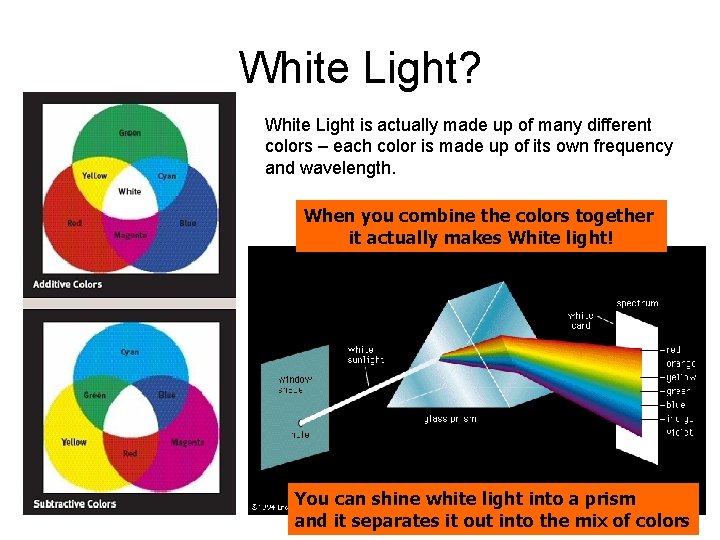
White Light? White Light is actually made up of many different colors – each color is made up of its own frequency and wavelength. When you combine the colors together it actually makes White light! You can shine white light into a prism and it separates it out into the mix of colors

Notice the white light coming in Notice the split spectrum coming out.

Types of Waves • Transverse (Shear) Waves • Longitudinal (Compression – Sound) Waves • Surface Waves – wave’s that move in a circular motion on the surface – (We will learn more about these during our geology unit. )

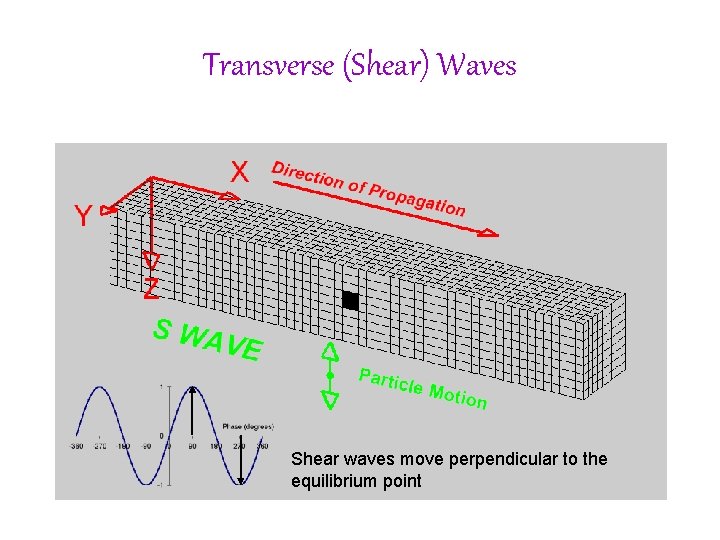
Transverse (Shear) Waves Shear waves move perpendicular to the equilibrium point

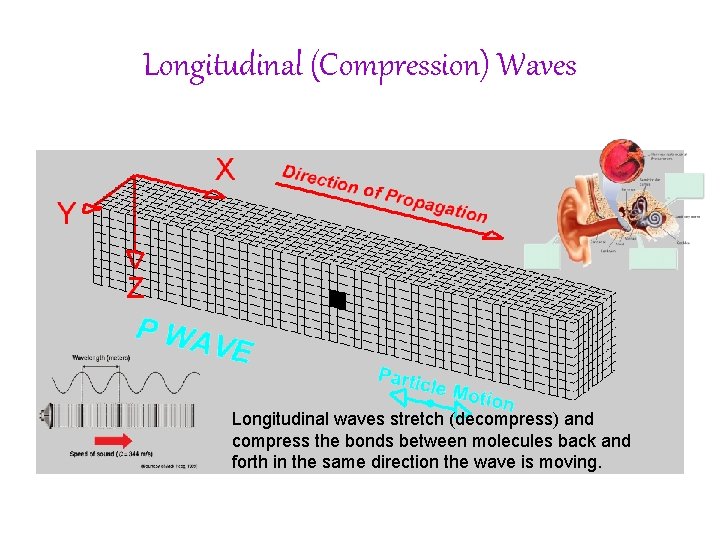
Longitudinal (Compression) Waves Longitudinal waves stretch (decompress) and compress the bonds between molecules back and forth in the same direction the wave is moving.

How do waves propagate away from its source? 2 Dimensionally or 3 Dimensionally

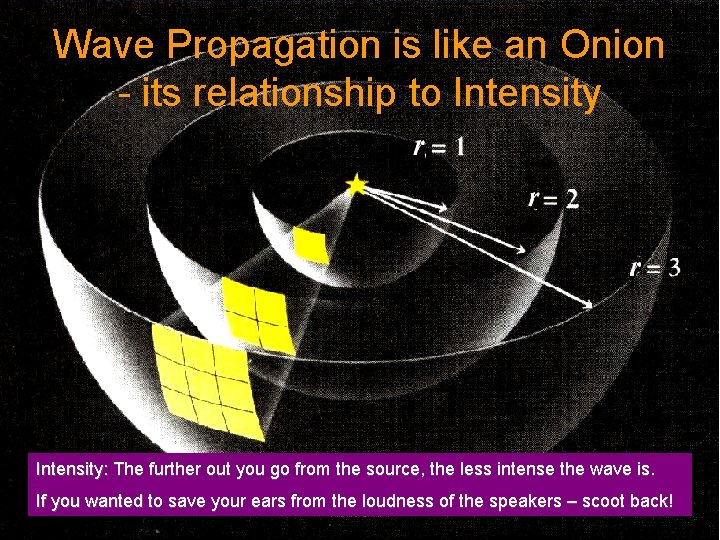
Propagation of Waves The layers of an onion, are a good representation of how waves look as they travel In every direction equally at the same time! HEY! I’ve got layers too!!! Except for surface waves, waves propagate outward spherically in 3 D - like the layers of an onion.

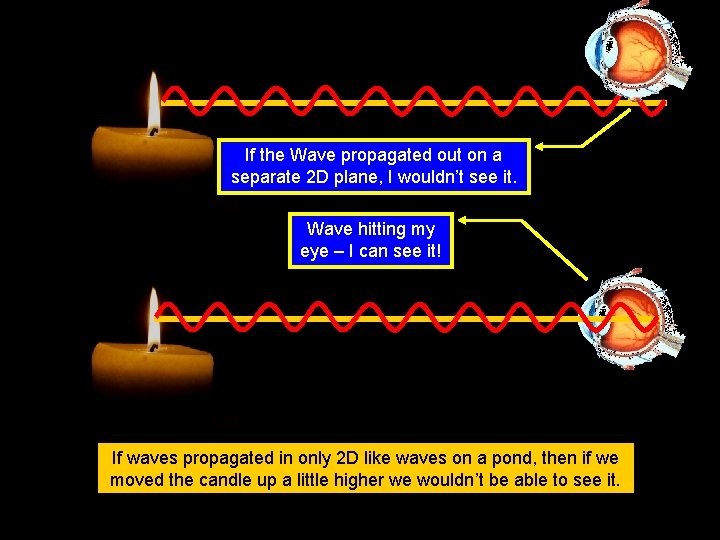
If the Wave propagated out on a separate 2 D plane, I wouldn’t see it. Wave hitting my eye – I can see it! If waves propagated in only 2 D like waves on a pond, then if we moved the candle up a little higher we wouldn’t be able to see it.

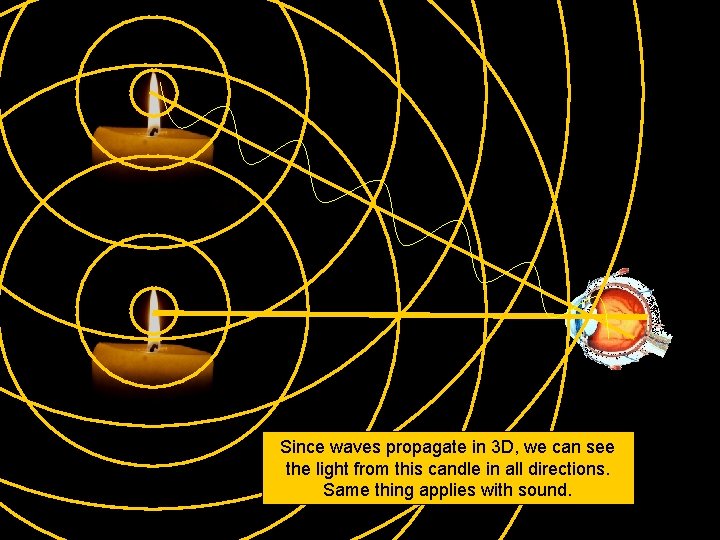
Since waves propagate in 3 D, we can see the light from this candle in all directions. Same thing applies with sound.

Wave Propagation is like an Onion - its relationship to Intensity: The further out you go from the source, the less intense the wave is. If you wanted to save your ears from the loudness of the speakers – scoot back!

Why we see something first – then hear it later

Wave Speed • Wave Speed = Frequency x Wavelength Speed = νλ 8 3. 0 x 10 m/s Light = Sound ≈ 340 m/s (Faster than most jets)

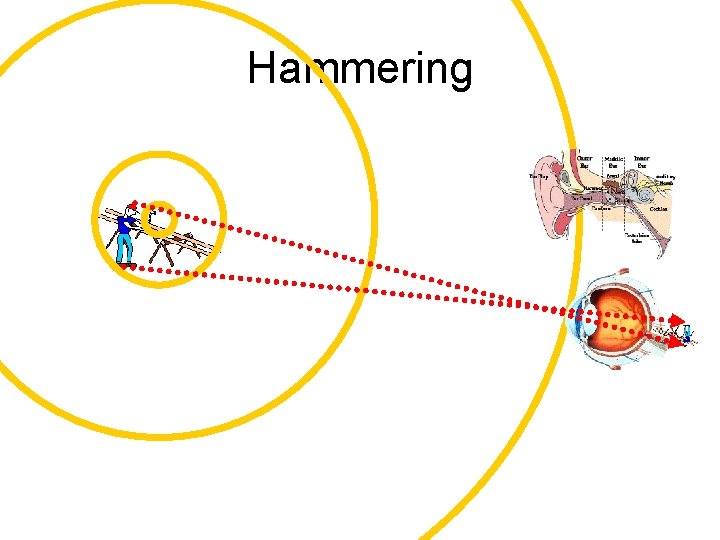
Hammering

Instruments to sense light energy

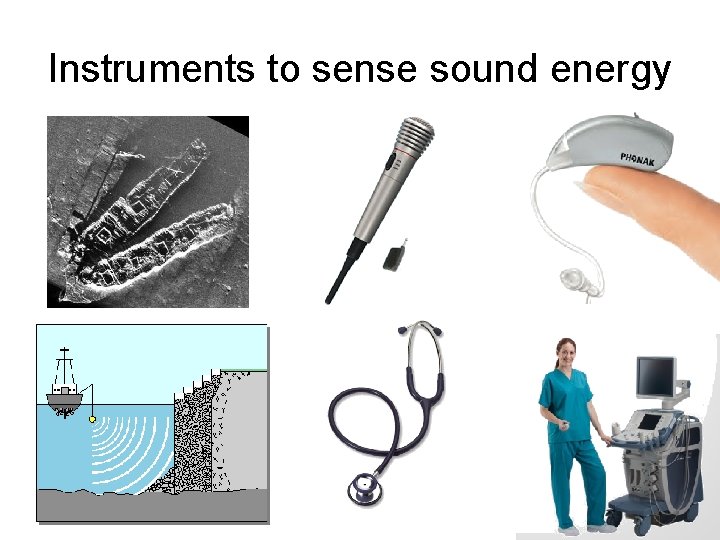
Instruments to sense sound energy