Wave Particle Nature of Light EQ How can

Wave & Particle Nature of Light EQ: How can an atom be a "particle" and a "wave" at the same time?

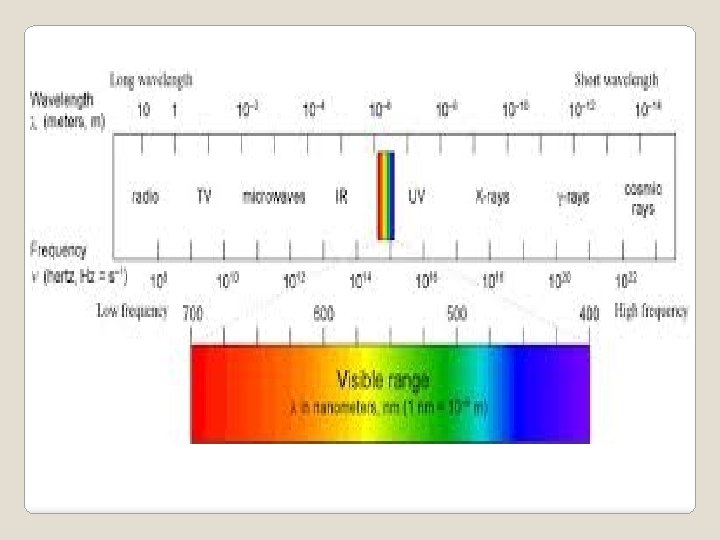
�Why do heated objects emit only certain frequencies of light? �Temperature of an object is a measure of the average kinetic energy of its particles �As an object gets hotter, it possess a greater amount of energy and emits different colors of light �Different colors are due to different frequencies and wavelengths Quantum Concept

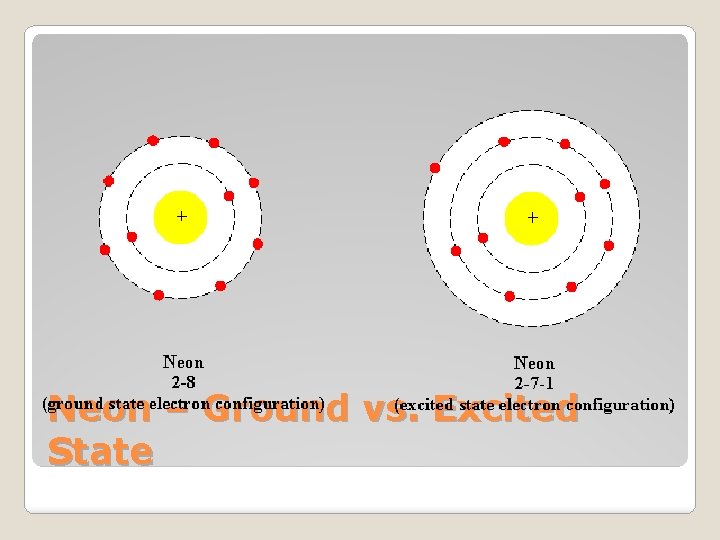
�Ground vs. Excited States of e- �Ground State: Lowest energy econfiguration ◦ Shown on Periodic Table ◦ Innermost energy level fills first, then work outward Ground State vs. Excited State

�Excited State: e- can move to a higher energy level without filling the lower energy level first ◦ Do this by absorbing energy �Excited e- fall back to ground state by releasing energy Ground State vs. Excited State

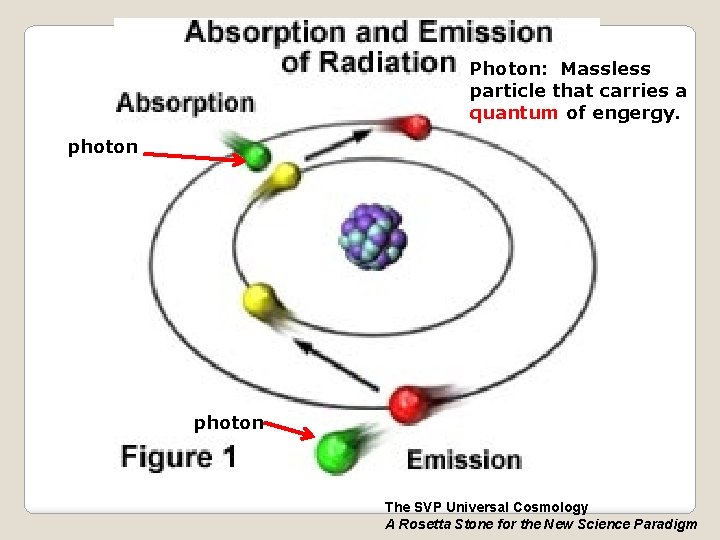
Photon: Massless particle that carries a quantum of engergy. photon The SVP Universal Cosmology A Rosetta Stone for the New Science Paradigm

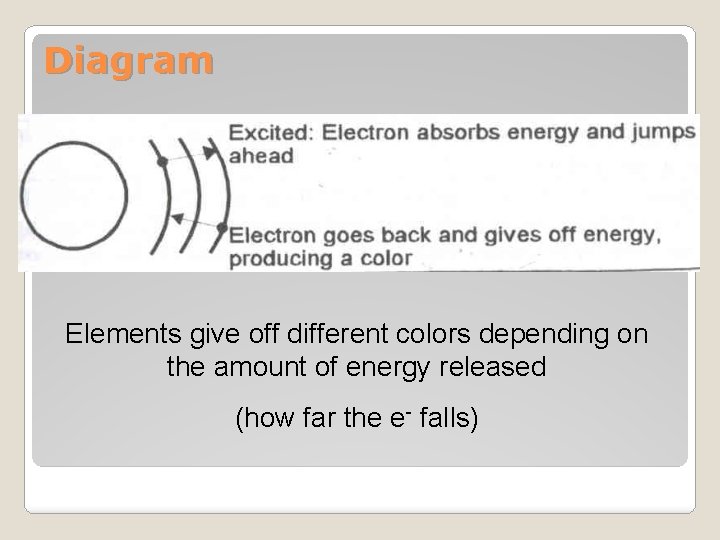
Diagram Elements give off different colors depending on the amount of energy released (how far the e- falls)

Neon – Ground vs. Excited State

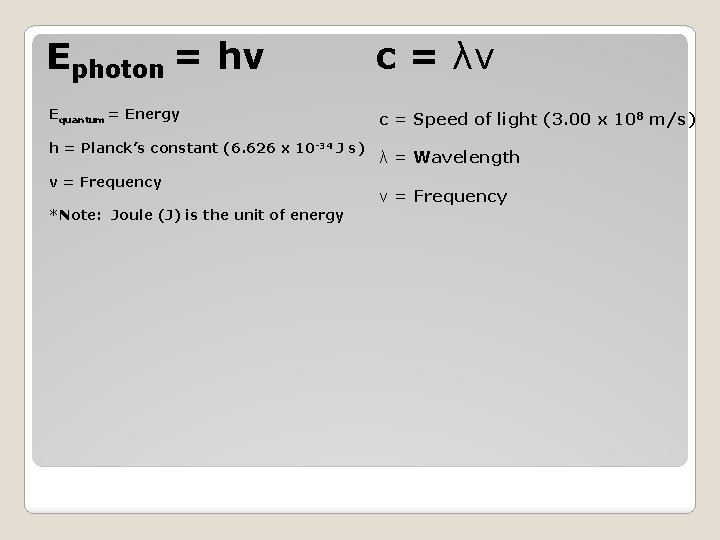
�German physicist Max Planck established that matter gains or loses energy in small amounts called quantum �Quantum is the minimum amount of energy that can be gained or lost by an atom. �Planck’s mathematical equation for his findings is Equantum = hv Quantum Concept

Ephoton = hv Equantum = Energy h = Planck’s constant (6. 626 x 10 -34 J s) v = Frequency *Note: Joule (J) is the unit of energy Quantum Concept

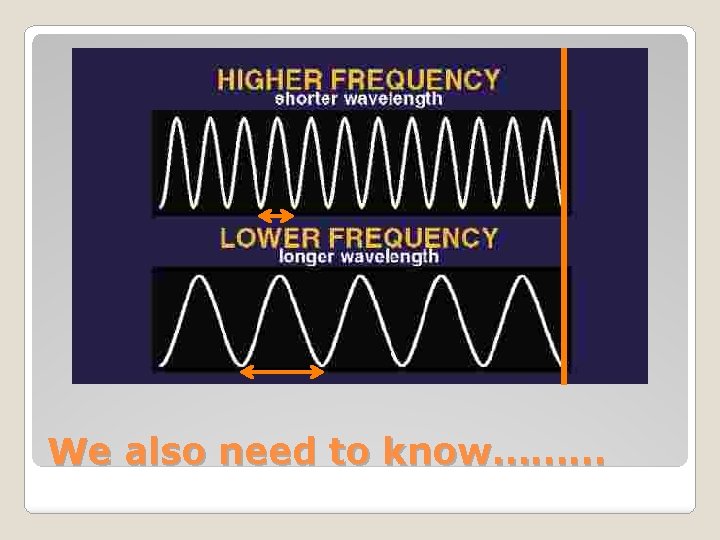
c = λv c = Speed of light (3. 00 x 108 m/s) λ = Wavelength (shortest distance between equivalent points on a wave) ν = Frequency (# of waves that pass a given point per second) We also need to know………

We also need to know………

Ephoton = hv c = λv v= c / λ What can we determine from these equations? As energy of a photon increases, the frequency increases and the wavelength decreases

Example: A photon is emitted from an atom with an energy of 5. 10 x 10 -20 J. What is the wavelength of the photon using correct significant figures? Ephoton = hv c = λv v = Ephoton / h v = 5. 10 x 10 -20 J / 6. 626 x 10 -34 J s v = 7. 69695 x 1013 s-1 λ=c/v λ = 3. 00 x 108 m/s / 7. 69695 x 1013 s-1 λ = 3. 89764 x 10 -6 m = 3. 90 x 10 -6 m

1. Ultraviolet radiation has a frequency of 6. 8 × 1015 s-1. Calculate the energy, in joules, of the photon. 2. Find the 4. 5 energy, x 10 -18 in. J joules, of microwave radiation with a frequency of 7. 91 × 1010 s-1. -23 J 3. A sodium vapor lamp emits light 5. 24 photons with a x 10 wavelength of 5. 89 × 10 -7 m. What is the energy of these photons? 4. One of the electron 3. 37 transitions x 10 -19 J in a hydrogen atom produces infrared light with a wavelength of 7. 464 × 10 -6 m. What amount of energy causes this transition? 2. 663 x 10 -20 J Solve & use correct number of sig. figs. (Rally Coach)

1. Find the energy in k. J for an x-ray photon with a frequency of 2. 4 × 1018 s-1. (1 k. J = 1000 J) 2. A ruby laser produces red light that has a wavelength of 500 nm. Calculate its energy in joules. (1 m = 1 000 000 nm) 3. What is the frequency of UV light that has an energy of 2. 39 × 10 -18 J? 4. What is the wavelength and frequency of photons with an energy of 1. 4 × 10 -21 J? Solve & use correct number of sig. figs.

Ephoton = hv c = λv Equantum = Energy c = Speed of light (3. 00 x 108 m/s) h = Planck’s constant (6. 626 x 10 -34 J s) v = Frequency *Note: Joule (J) is the unit of energy λ = Wavelength ν = Frequency