WAVE OPTICS WAVE OPTICS MALUS LAW WAVE OPTICS

WAVE OPTICS

WAVE OPTICS MALUS LAW

WAVE OPTICS Malus Law Ø If I 0 be the intensity of the polarized light incident on the analyzer and be the angle between the transmission axes of the polarizer and analyzer, then the intensity of the light transmitted through the analyzer is given by, I= I 0 cos 2 Ø If A be the amplitude of the light transmitted through the analyzer and A 0 be the amplitude of the polarized light incident on it, then

WAVE OPTICS Ø If Ii be the intensity of the unpolarized light incident on the polarizer and I be the intensity of the light transmitted through the analyzer, then I = I 0 cos 2 Here I 0 = Ii /2 Ø In the above expressions is also angle between the plane of oscillation of the polarized light and the transmission axes of the analyzer.

WAVE OPTICS Ø For the crossed polarizer and analyzer, =900 hence : I= I 0 cos 2 900 =0 Ø Polarization confirms the transverse nature of the light waves. Ø Light can be polarized by the following methods (i) reflection (ii) refraction (iii) double refraction (iv) dichorism (v) scattering

WAVE OPTICS MCQ S 1. Polarization confirms the. . . nature of light waves. a) transverse b) longitudinal c) both (a) and (b) d) none of above

WAVE OPTICS 2. Which of the following method can be used for polarization of light? a) reflection b) refraction c) double refraction d) all the above

WAVE OPTICS BREWSTER’S LAW

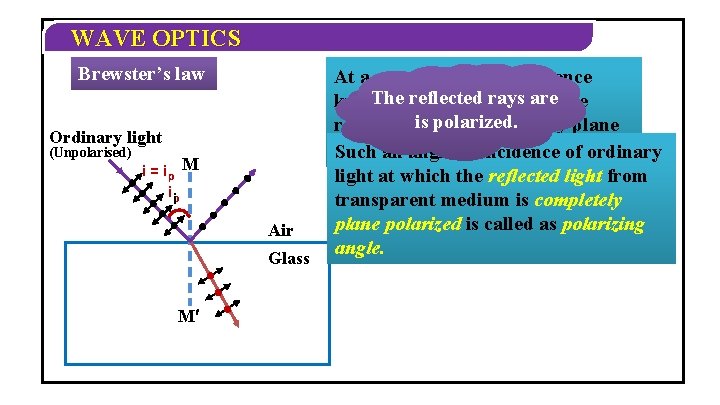
WAVE OPTICS Brewster’s law Ordinary light (Unpolarised) i = ip M ipi Air Glass M At a certain angle of incidence While isangle The rays Part ofthe therest light isare the known asreflected polarizing isreflected. polarized. reflectedrefracted. light is completely plane polarised in theofplane of incidence. Such an angle incidence of ordinary light at which the reflected light from transparent medium is completely plane polarized is called as polarizing angle.

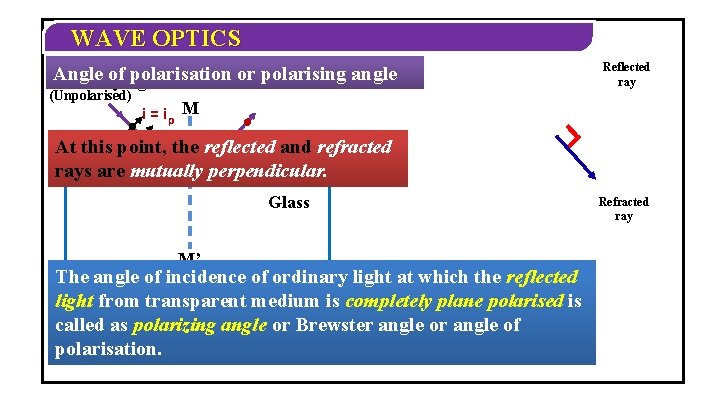
WAVE OPTICS Angle of light polarisation or polarising angle Ordinary (Unpolarised) Reflected ray i = ip M ip At this point, the reflected and refracted rays are mutually perpendicular. Air Glass M’ The angle of incidence of ordinary light at which the reflected light from transparent medium is completely plane polarised is called as polarizing angle or Brewster angle of polarisation. Refracted ray

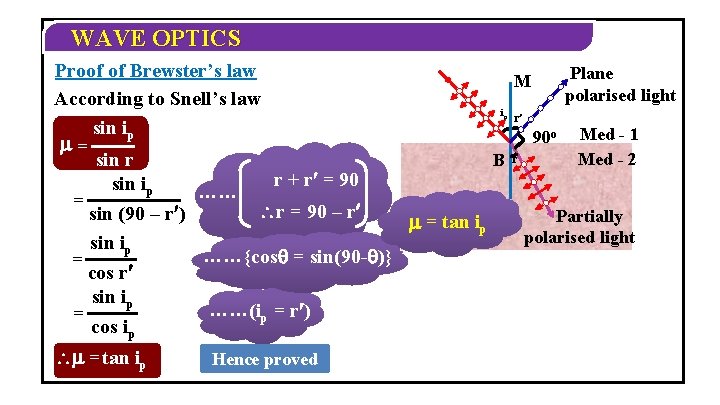
WAVE OPTICS Proof of Brewster’s law According to Snell’s law sin ip = sin r r + r = 90 sin ip …… = r = 90 – r sin (90 – r ) sin ip = cos r sin ip = cos ip = tan ip ……{cos = sin(90 - )} ……(ip = r ) Hence proved Plane polarised light M ip r’ 90 o B = tan ip M r Med - 1 Med - 2 Partially polarised light

WAVE OPTICS 1. According to Brewster’s law. . . a) sin i = sin r b) = c) sin r sin i = tan ip d) = 1 tan ip MCQ S

WAVE OPTICS 2. At polarising angle, the angle between reflected and refracted rays is. . . a) 0° b) 45° c) 180° d) 90°

WAVE OPTICS 3. At polarising angle, the incident un-polarised light is reflected as. . . a) a plane polarised light b) an un-polarised light c) a partially polarised light d) none of the above

WAVE OPTICS YOUNG’S DOUBLE SLIT EXPERIMENT

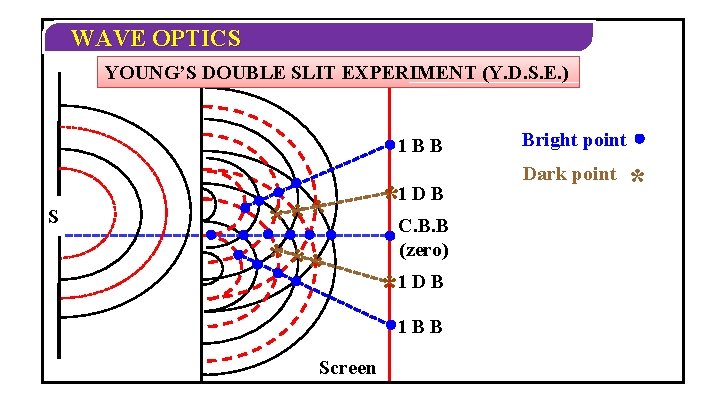
WAVE OPTICS YOUNG’S DOUBLE SLIT EXPERIMENT (Y. D. S. E. ) 1 BB S *** * 1 DB C. B. B (zero) *1 D B 1 BB Screen Bright point Dark point *

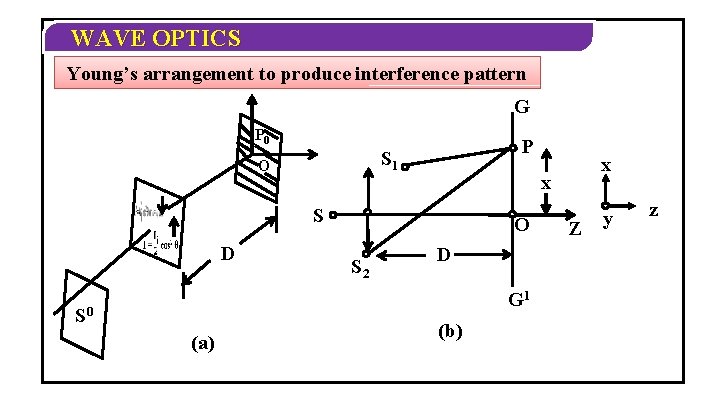
WAVE OPTICS YOUNG’S DOUBLE SLIT EXPERIMENT (Y. D. S. E. ) Ø Thomas young used an ingenious technique to “lock” the phases of the waves emanating from S 1 and S 2. Ø He made two pinholes S 1 and S 2 (very close to each other) on an opaque screen. Ø These were illuminated by another pinhole that was in turn lit by a bright source. Ø Light waves spread out from S and fall on both S 1 and S 2.

WAVE OPTICS Young’s arrangement to produce interference pattern G P 0 P S 1 O x S D O S 2 D G 1 S 0 (a) x (b) Z y z

WAVE OPTICS Ø S 1 and S 2 then behave like two coherent sources because light waves coming out from S 1 and S 2 are derived from the same original source and any abrupt phase change in S will manifest in exactly similar phase changes in the light coming out from S 1 and S 2. They Thus, willthe be two coherent like sources the two S 1 and vibrating S 2 will needles be locked in a water in phase. wave.

WAVE OPTICS Ø Thus spherical waves (or spherical wave front) eliminating from S 1 and S 2 will produce interference fringes on the screen GG. Ø The positions of maximum and minimum intensities can be calculated by using the analysis given that for an arbitrary point P on the line GG to correspond to a maximum. S 2 P – S 1 P = n ; n= 0, 1, 2, . . . . Now, (1)

WAVE OPTICS Where S 1 S 2 = d and OP = x. Thus

WAVE OPTICS If x, d<<D then negligible error will be introduced if S 2 P + S 1 P (in the denominators) is replaced by 2 D. for example, for d=0. 1 cm, D= 100 cm, OP= 1 cm (which correspond to typical values for an interference experiment using light waves), we have S 2 P + S 1 P = [(100)2 +(1. 05)2]1/2 + [(100)2 +(0. 95)2]1/2 = 200. 01 cm

WAVE OPTICS Ø Thus if we replace S 2 P + S 1 P by 2 D, the error involved is about 0. 005%. Ø In this approximation, equation (2) becomes Ø Hence, we will have constructive interference resulting in a bright region when

WAVE OPTICS Ø On the other hand, we will have a dark region near Ø Thus, dark and bright bands appear on the screen, such bands are called fringes.

WAVE OPTICS Ø When D>>d and white light source is used, then the wavelength absent infront of one of the source will be

WAVE OPTICS Ø The distance between two conjugative bright and dark fringes is given by = xn+1 - xn Ø Which is the expression for the fringe width.

WAVE OPTICS

WAVE OPTICS Ø The bright fringes are the result of constructive interference where as dark fringes are the result of destructive interference. Ø The central fringe is bright with monochromatic light where as it is achromatic(white) with white light. Ø The formation of fringes is explained on the basis of the Huygen’s wave theory of light.

WAVE OPTICS 1. In Young’s double slit experiment sodium vapour lamp is replaced by neon lamp. Then the fringe width. . . . MCQ S a) increases b) decreases c) remain same d) becomes zero

WAVE OPTICS 2. A fringe is a locus of. . a) constant amplitude b) constant intensity c) constant phase d) same wavelength

WAVE OPTICS 3. Young’s experiment establishes that. . a) light consists of waves b) light consists of photons c) light consists of corpuscles d) light has dual nature

WAVE OPTICS Thank you…