WAVE OPTICS WAVE OPTICS CONCEPT OF INTERFERENCE WAVE

WAVE OPTICS

WAVE OPTICS CONCEPT OF INTERFERENCE

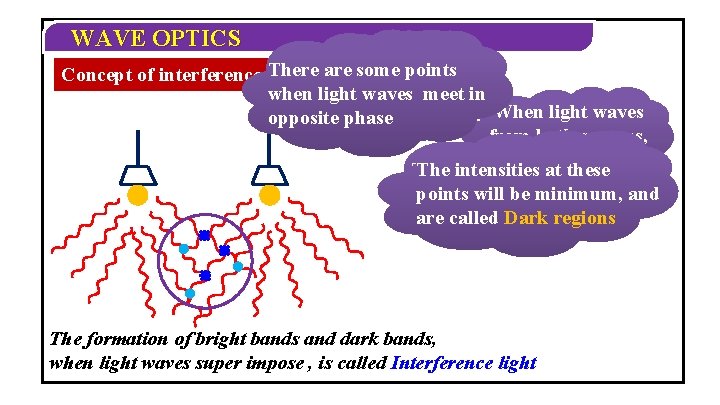
WAVE OPTICS some Thereare somepoints Consider two Concept of interference There when waves meet in when light waves light sources When light waves opposite phase in same phase from both sources, superimpose Theintensities atthesepoints The at points will be minimum, will be maximum, and are called Dark regions called bright region. The formation of bright bands and dark bands, when light waves super impose , is called Interference light

WAVE OPTICS Interference pattern of light Simple pattern Complex pattern (Stationary pattern) (Sustained pattern) (Steady state pattern)

WAVE OPTICS How do we get steady state pattern ? There a few conditions which have to be followed to get a steady state pattern. Before we understand the conditions, lets visualize the steady state pattern.

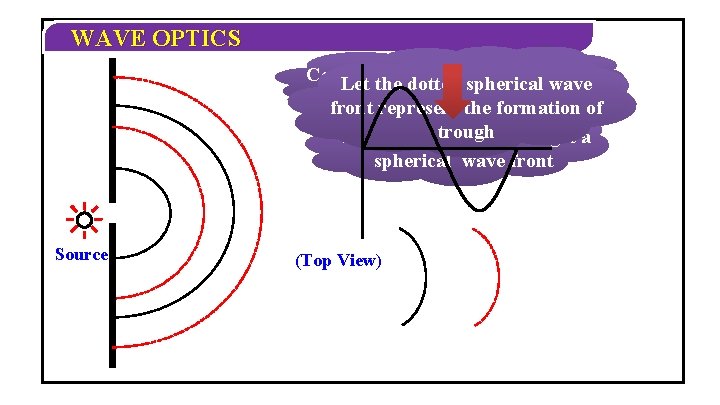
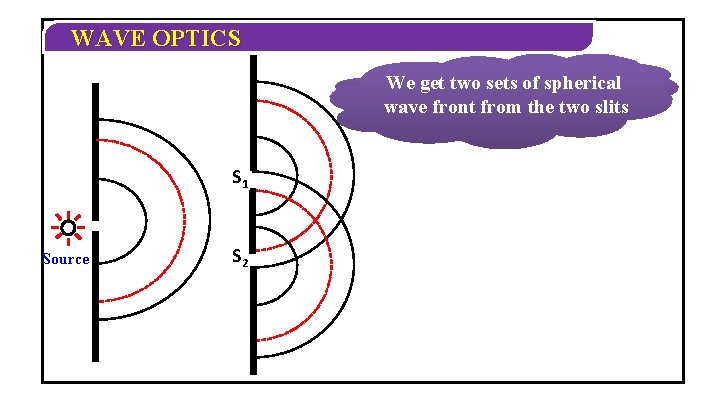
WAVE OPTICS Consider a monochromatic source Letthe dotted spherical wave Let continuous spherical wave front represent the formationofof When a slit trough iscrest placed, we get a spherical wave front Source (Top View)

WAVE OPTICS We suppose get two sets of spherical Now if two slits are kept wave front from the two slits S 1 Source S 2

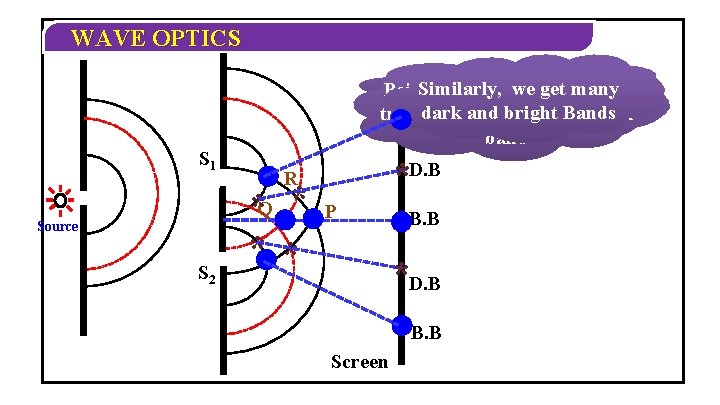
WAVE OPTICS S 1 Source S 2 Let S 1 & S 2 crest be two slits Similarly, wethe get many Point ‘R’ has meeting aa aa The point ‘P’ has Point The point ‘Q’ will ‘P’ also will be be What about point R? dark and bright Bands trough, i. e. it would be a dark B. B crestbright meeting crest band *D. B R *Q * ** P B. B *D. B B. B Screen

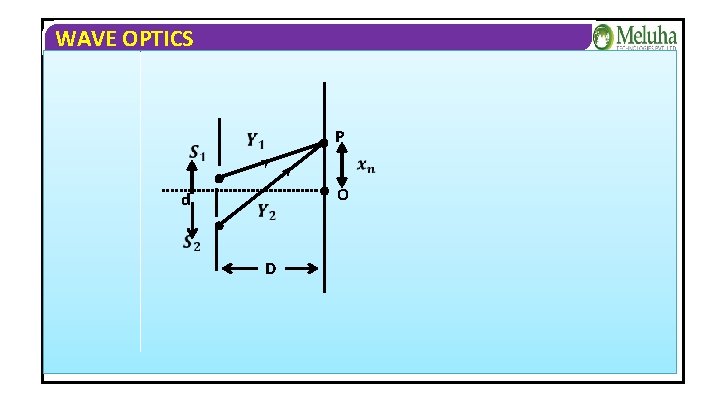
WAVE OPTICS The redistribution of energy due to super imposition of two or more waves is called interference. Derivation for interference pattern: They interfere at a point ‘P’ on the screen. Their equations are given by Where ∅ is the phase difference between two waves

WAVE OPTICS P > > O d D

WAVE OPTICS The resultant wave equation is given by

WAVE OPTICS The above equation represents S. H. M and its amplitude is R squaring and adding equations (1) and (2), we get

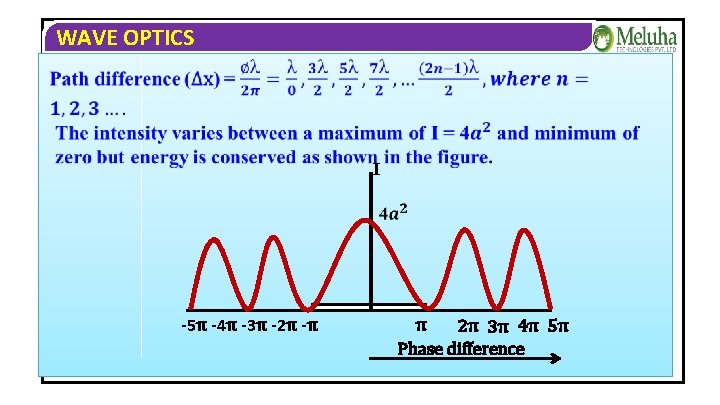
WAVE OPTICS Condition for maximum intensity or bright fringe. ∅=0, 2�� , 4�� , 6�� , 8�� , …. . , 2 n�� Path difference (∆x)=0, , 2 , …. n , where n=0, 1, 2, 3, …. . Condition for minimum intensity or dark fringe.

WAVE OPTICS I -5π -4π -3π -2π -π π 2π 3π 4π 5π Phase difference

WAVE OPTICS 1. The pattern in which, the position of bright and dark bands are fixed is called. . a) steady state pattern b) turbulence c) complex pattern d) streamline MCQ S

WAVE OPTICS 2. The steady pattern consists of alternate. . . . . a) waxing & waving b) bright band & dark band c) compensation & rarefaction d) crest & trough

WAVE OPTICS 3. The phenomenon of formation of bright and dark band, for light waves is called. . . . . a) diffraction b) polarization c) interference d) reflection

WAVE OPTICS CONCEPT OF BANDWIDTH

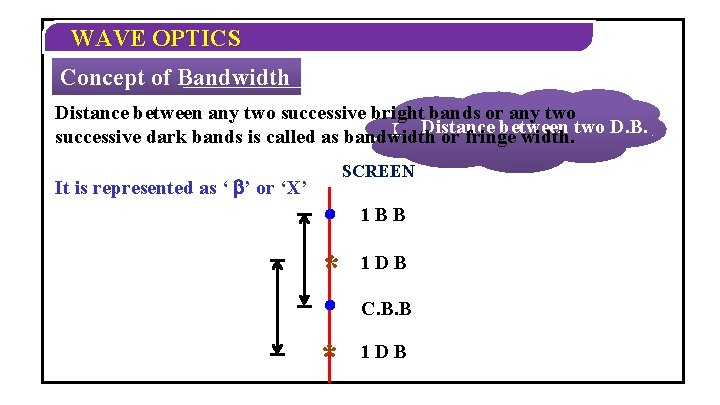
WAVE OPTICS Concept of Bandwidth Distance between any two successive bright bands or any two Distance between anytwo two. D. B. B. B. successive dark bands is called as bandwidth or fringe width. SCREEN It is represented as ‘ ’ or ‘X’ 1 BB * 1 DB C. B. B * 1 DB

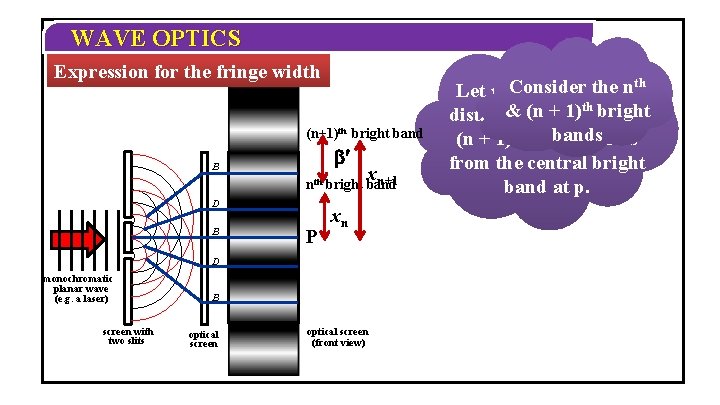
WAVE OPTICS Expression for the fringe width th (n+1)th bright band ¢ B x n+1 nth bright band D B P xn D monochromatic planar wave (e. g. a laser) screen with two slits B optical screen thethe n Let xn Consider and xn+1 be Consider the & (n 1)thcentral bright distances of+the nth and bright point as P bands (n + 1)th bright bands from the central bright band at p. optical screen (front view)

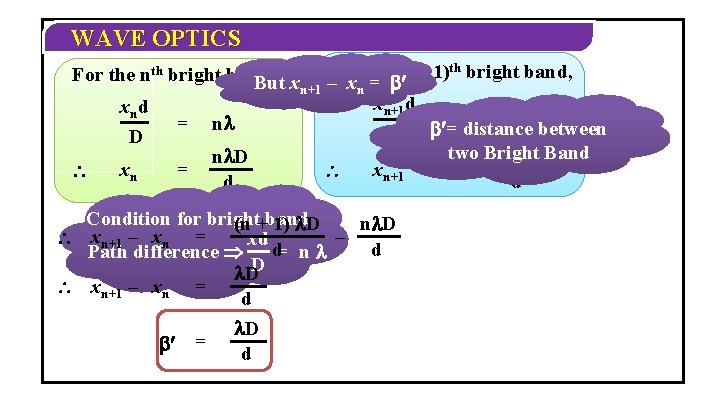
WAVE OPTICS For the (n + 1)th bright band, n+1 – xn = ¢ xn+1 d = (n + 1) D ¢= distance between two (n. Bright + 1) DBand xn+1 = d For the nth bright band, But x xnd D xn = n D d Condition for bright (n +band 1) D n D – xn+1 – xn = xd d Path difference Þ d= n DD xn+1 – xn = d D ¢ = d

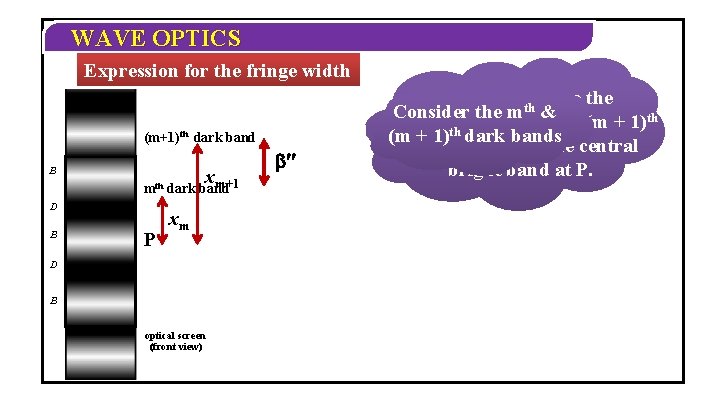
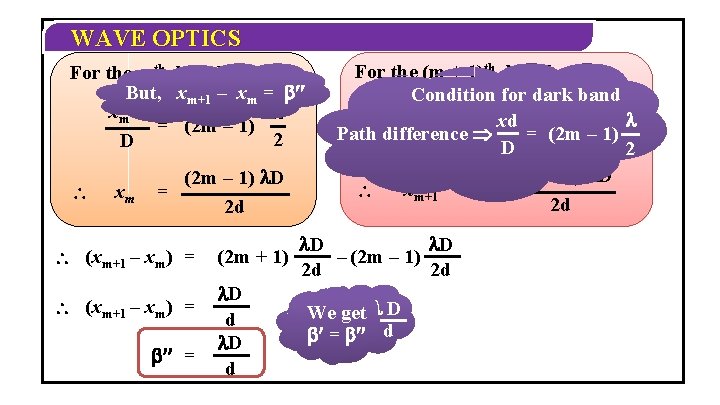
WAVE OPTICS Expression for the fringe width (m+1)th dark band B mth D B P xm+1 dark band xm D B optical screen (front view) ¢¢ Let xm and xthm+1 be the Consider the mnth &central th Consider the distances of the and (m + 1) th dark bands (m + 1) brightfrom pointthe as central P dark bands bright band at P.

WAVE OPTICS For the mth dark band, But, xm+1 – xm = ¢¢ xmd = (2 m – 1) 2 D xm (2 m – 1) D = 2 d (xm+1 – xm) = ¢¢ = (2 m + 1) D d For the (m + 1)th dark band, Condition for dark band xm+1 d =xd[2(m + 1) – 1] Path difference Þ = (2 m – 1) 2 D D 2 (2 m + 1) D = xm+1 2 d D D – (2 m – 1) 2 d 2 d We get D But ¢ = ¢¢ d

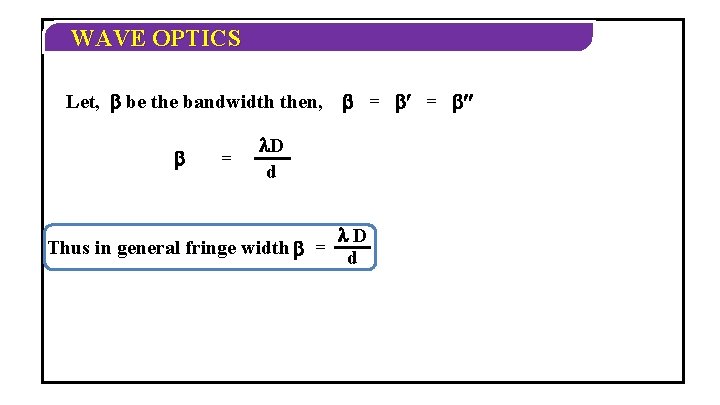
WAVE OPTICS Let, be the bandwidth then, = = ¢¢ D d Thus in general fringe width = D d

WAVE OPTICS 1. Distance between the two successive B. B’s or D. B’s is called as. . . . a) Phase difference b) Interference c) Path difference d) Bandwidth MCQ S

WAVE OPTICS 2. If the wavelength of monochromatic light used in Y. D. S. E, is increased, the bandwidth …. . a) increases b) decreases c) remains same d) depends of medium

WAVE OPTICS 3. For a steady state interference pattern, the distance between the two sources or slits should be…. . a) very small b) sufficiently large c) very large d) infinite

WAVE OPTICS CONDITIONS FOR A STEADY INTERFERENCE PATTERN

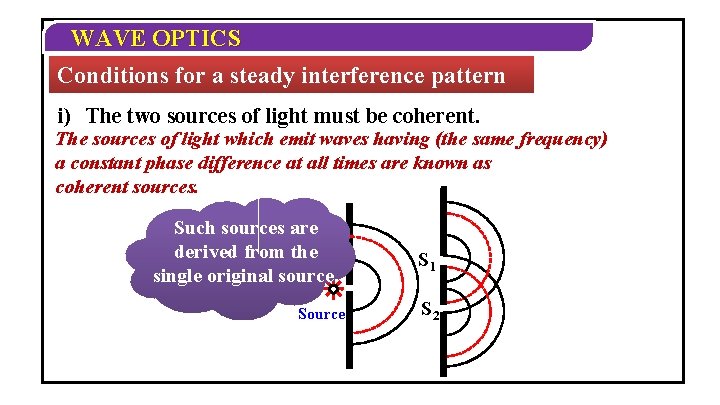
WAVE OPTICS Conditions for a steady interference pattern i) The two sources of light must be coherent. The sources of light which emit waves having (the same frequency) a constant phase difference at all times are known as coherent sources. Such sources are derived from the single original source. Source S 1 S 2

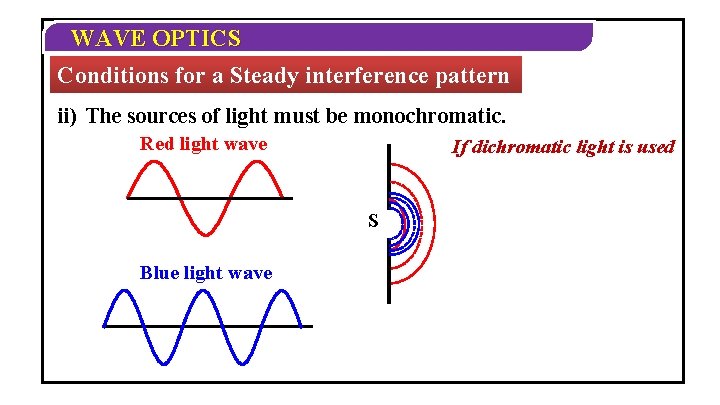
WAVE OPTICS Conditions for a Steady interference pattern ii) The sources of light must be monochromatic. Red light wave If dichromatic light is used S Blue light wave

WAVE OPTICS Conditions for a steady interference pattern ii) The sources of light must be monochromatic. If the sources emit light waves of more than one wavelength, then at one point there may be constructive interference due to light of one wavelength and destructive interference due to other wavelength. Also, the no. of bright and dark bands will increase. Hence, pattern will be complex and colourful.

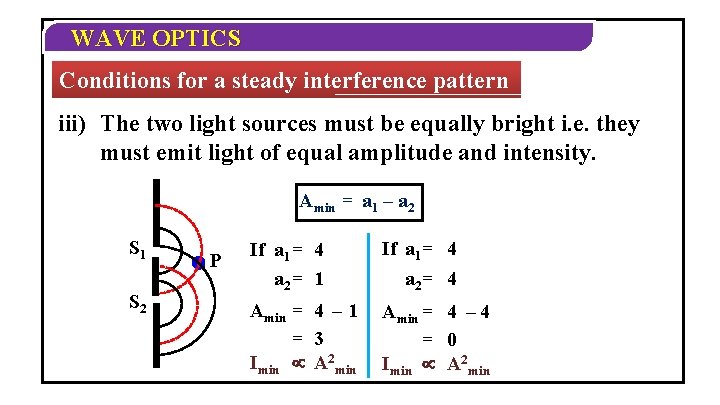
WAVE OPTICS Conditions for a steady interference pattern iii) The two light sources must be equally bright i. e. they must emit light of equal amplitude and intensity. Amin = a 1 – a 2 S 1 S 2 P If a 1 = 4 a 2 = 1 If a 1= 4 a 2= 4 Amin = 4 – 1 = 3 Imin A 2 min Amin = 4 – 4 = 0 Imin A 2 min

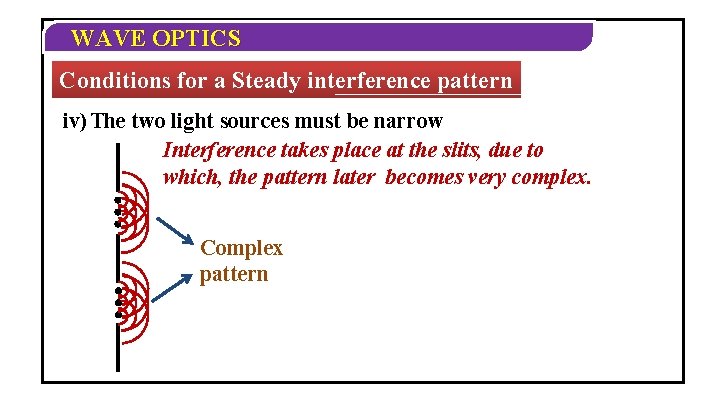
WAVE OPTICS Conditions for a Steady interference pattern iv) The two light sources must be narrow Interference takes place at the slits, due to which, the pattern later becomes very complex. Complex pattern

WAVE OPTICS Conditions for a steady interference pattern v) The two sources should be close to each other S 1 S 2

WAVE OPTICS Conditions for a Steady interference pattern vi) The two sources should be at sufficiently large distance from the screen. Screen S 1 S 2 Distance between source & screen

WAVE OPTICS The distance between two consecutive bright or consecutive dark fringes is known as fringe width ��. Angular fringe width( ): It has no unit.

WAVE OPTICS Dependence of fringe width:

WAVE OPTICS Fringe visibility (V): With the half of visibility, knowledge about coherence, fringe contrast and interference pattern will be visible.

WAVE OPTICS Resultant intensity:

WAVE OPTICS

WAVE OPTICS Ø When one of the slits is closed and width of another is made of the order of , then diffraction fringes are observed.

WAVE OPTICS 1. When the phase difference between two sources of light is fixed, they are said to be…… a) non - coherent b) mono chromatic c) coherent d) polychromatic MCQ S

WAVE OPTICS 2. For a steady state pattern, the two sources should be…. . a) big sources b) narrow Sources c) wide sources d) none of these

WAVE OPTICS 3. If the two sources have same amplitude/intensity then, the steady pattern has…. . a) no contrast b) low contrast c) complex fringes d) high contrast

WAVE OPTICS 4. For a steady state pattern, the distance between the sources and screen should be…. . a) very small b) infinite c) sufficiently large d) finite

WAVE OPTICS CONSTRUCTIVE AND DESTRUCTIVE PATTERN

WAVE OPTICS Interference of light Constructive pattern Destructive pattern (Bright Band) (Dark Band)

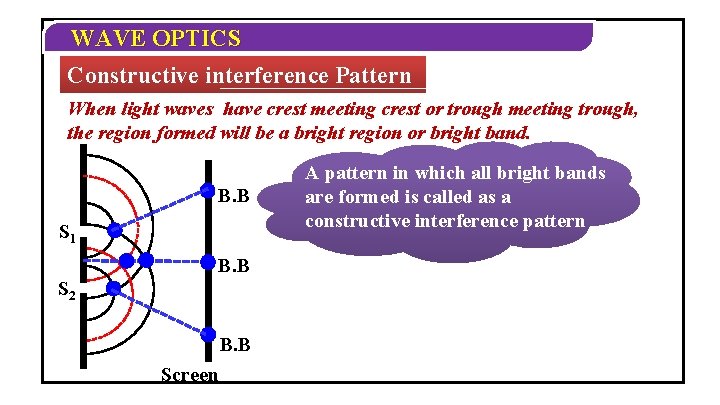
WAVE OPTICS Constructive interference Pattern When light waves have crest meeting crest or trough meeting trough, the region formed will be a bright region or bright band. B. B S 1 B. B S 2 B. B Screen A pattern in which all bright bands are formed is called as a constructive interference pattern

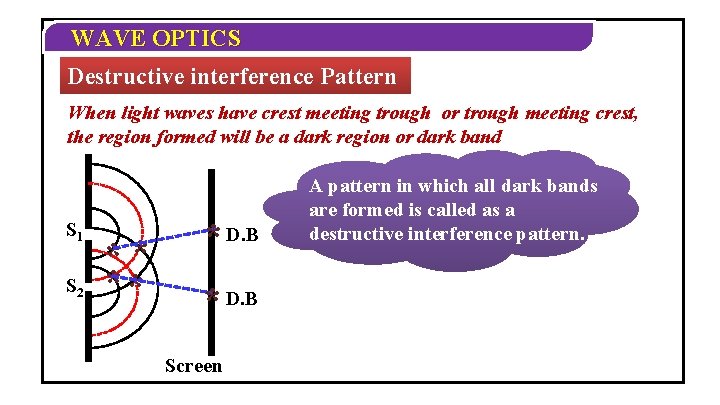
WAVE OPTICS Destructive interference Pattern When light waves have crest meeting trough or trough meeting crest, the region formed will be a dark region or dark band S 1 S 2 ** ** * D. B Screen A pattern in which all dark bands are formed is called as a destructive interference pattern.

WAVE OPTICS Conditions for constructive destructive interference of light Constructive interferenceand (brightness) (i) For a bright band, a crest of one wave should meet the crest of another wave or trough of one wave should meet the trough of another wave. C. B. B 1 st B. B (ii) Phase difference : 0, 2 , 4 , 6 , ……. . = 2 n (iii) Path difference : 0, , 2 , 3 , ……. . = n (Where, n = 0 , 1, 2…)

WAVE OPTICS Conditions for constructive and destructive interference of light (2) Destructive interference (darkness) (i) For a dark band , a crest of one wave should meet the trough of another wave. 2 nd D. B 1 st D. B (ii) Phase difference : , 3 , 5 , …. . = (2 m– 1) (iii)Path difference : 3 5 , , , …. . = (2 m– 1) 2 2 (Where, m = 1 , 2, 3… )

WAVE OPTICS 1. A point on a steady state pattern has a phase difference of ‘ 5 ’, it is a. . . . a) 4 th D. B. b) 4 th B. B. c) 3 rd D. B. d) 3 rd B. B. MCQ S

WAVE OPTICS Solution : Phase difference = (2 m – 1) Phase difference = 5 (2 m – 1) 2 m = 5+1 6 m = 2 m = 3

WAVE OPTICS 2. The path difference of a 10 th D. B in a steady state pattern is. . . 13 a) 2 11 b) 2 c) 19 2 d) 5 2

WAVE OPTICS Solution : Path difference 2 = (20 – 1) 2 19 = 2 = (2 m – 1) …(m = 10)

WAVE OPTICS Thank you…