Wave Functions of the Electron in a Hydrogen

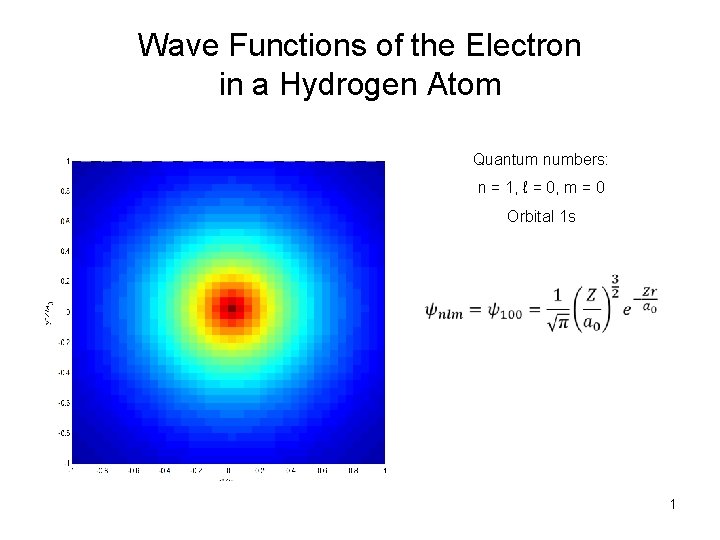
Wave Functions of the Electron in a Hydrogen Atom Quantum numbers: n = 1, ℓ = 0, m = 0 Orbital 1 s 1

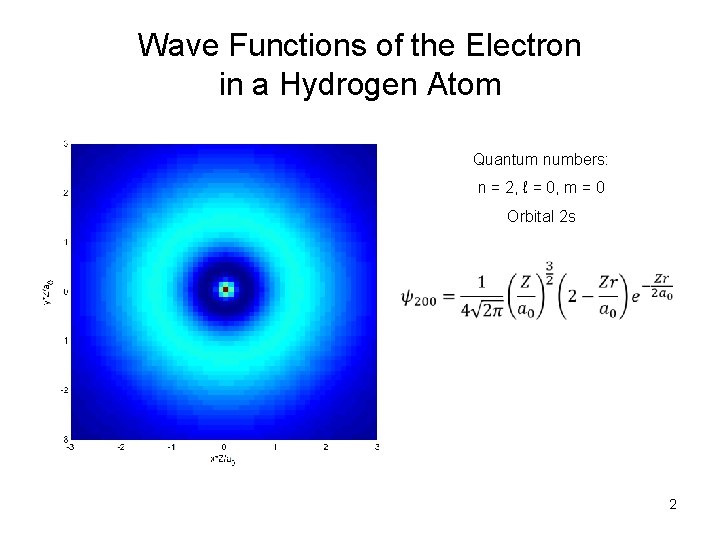
Wave Functions of the Electron in a Hydrogen Atom Quantum numbers: n = 2, ℓ = 0, m = 0 Orbital 2 s 2

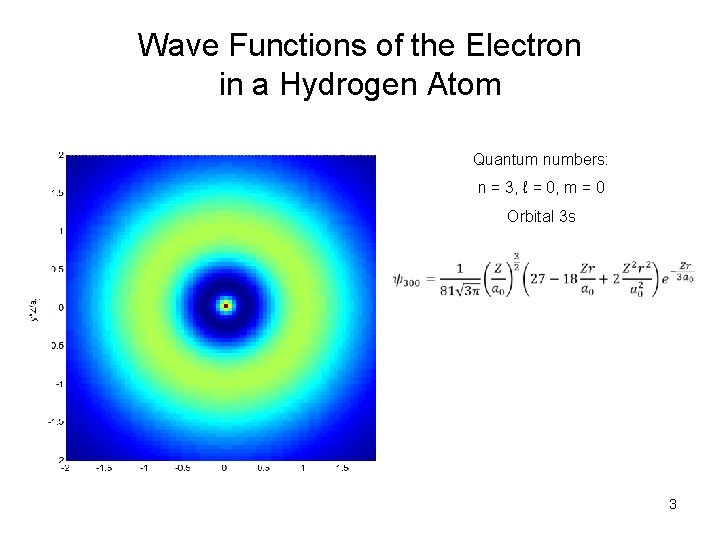
Wave Functions of the Electron in a Hydrogen Atom Quantum numbers: n = 3, ℓ = 0, m = 0 Orbital 3 s 3

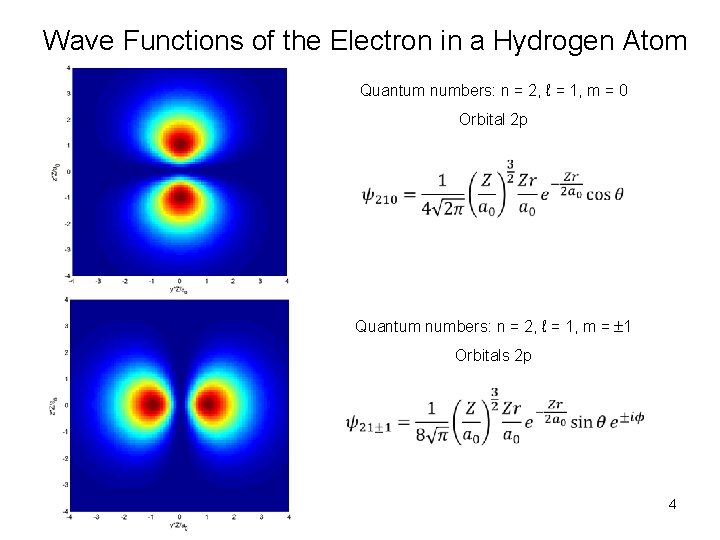
Wave Functions of the Electron in a Hydrogen Atom Quantum numbers: n = 2, ℓ = 1, m = 0 Orbital 2 p Quantum numbers: n = 2, ℓ = 1, m = 1 Orbitals 2 p 4

Wave Functions of the Electron in a Hydrogen Atom Quantum numbers: n = 3, ℓ = 1, m = 0 Orbital 3 p Quantum numbers: n = 3, ℓ = 1, m = 1 Orbital 3 p 5

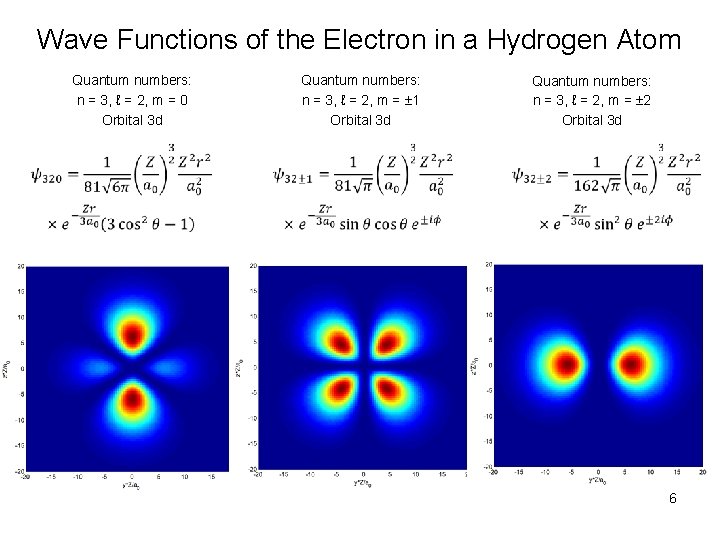
Wave Functions of the Electron in a Hydrogen Atom Quantum numbers: n = 3, ℓ = 2, m = 0 Orbital 3 d Quantum numbers: n = 3, ℓ = 2, m = 1 Orbital 3 d Quantum numbers: n = 3, ℓ = 2, m = 2 Orbital 3 d 6

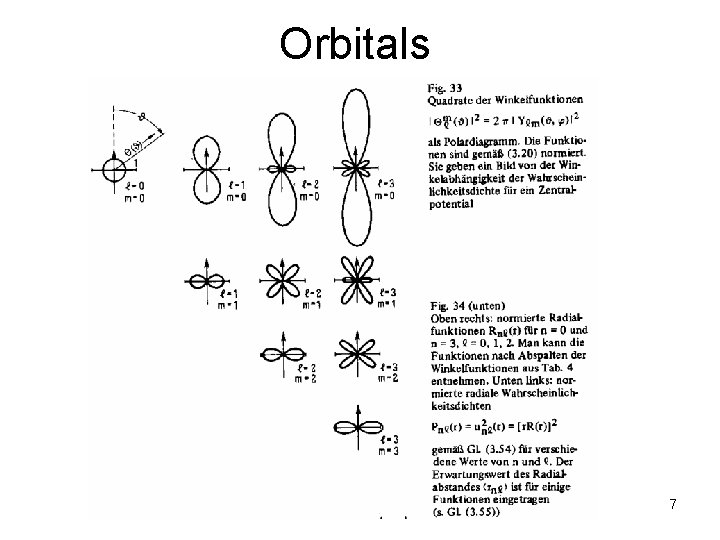
Orbitals 7

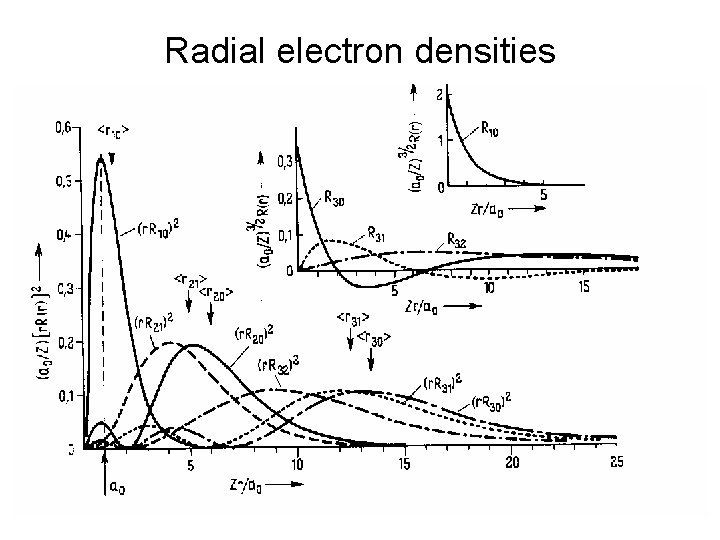
Radial electron densities 8

Hydrogen-like Atoms H, He+, Li++ (having 1 electron) Energy levels Spectral series of hydrogen … Lyman Energy level difference … Balmer … Paschen … Brackett … Pfund 9

Spectral series of Hydrogen Lyman (UV): n 2 3 4 l (nm) 121. 5 102. 5 97. 2 91. 2 Balmer: n 3 4 5 l (nm) 656. 3 486. 2 434. 1 364. 6 Paschen (IR): n 4 5 6 l (mm) 1. 875 1. 282 1. 094 0. 820 10

Moseley's law … correction for shielding by other electrons From theory (for a hydrogen-like atom) 11

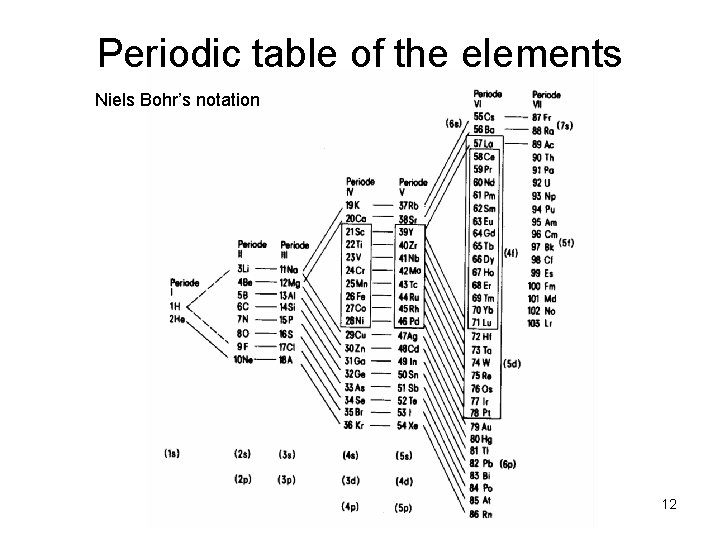
Periodic table of the elements Niels Bohr’s notation 12

Periodic table of the elements 13

Nuclear Shell Model For atoms with more than one electron (above hydrogen) Order of the energy levels Orbital quantum numbers s p d f g �= 0 1 2 3 4 (2� +1) = 1 3 5 7 9 2(2� +1) = 2 6 10 14 18 14

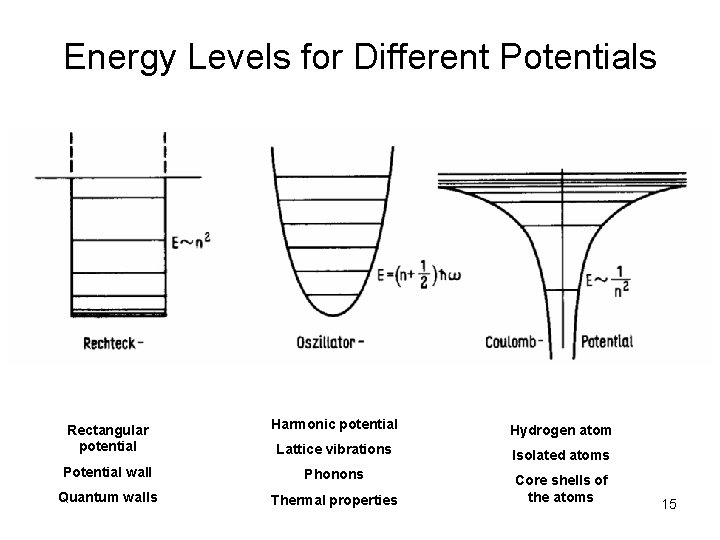
Energy Levels for Different Potentials Fig. 29, Seite 70 Rectangular potential Harmonic potential Hydrogen atom Lattice vibrations Isolated atoms Potential wall Phonons Quantum walls Thermal properties Core shells of the atoms 15