Wave Cluster A multiresolution clustering approach q Apply

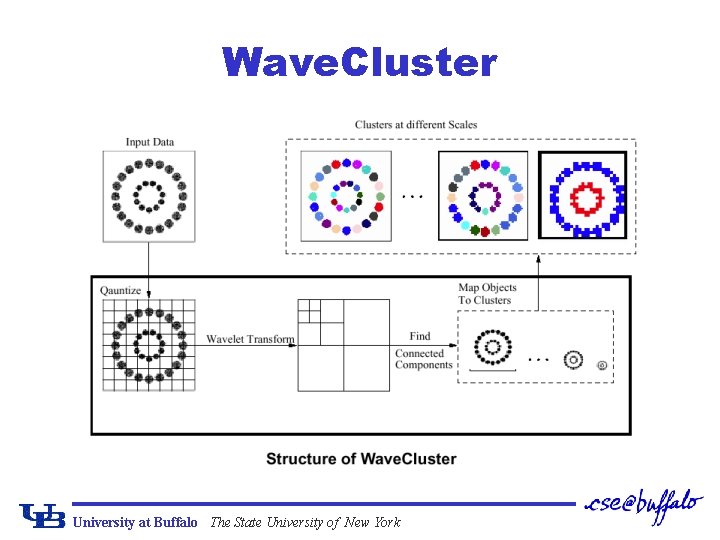
Wave. Cluster ¢ A multi-resolution clustering approach q Apply wavelet transformation to the feature space ¢ Both grid-based and density-based ¢ Input parameters: q Number of grid cells for each dimension q The wavelet q The number of applications of wavelet transform University at Buffalo The State University of New York

What are Wavelets University at Buffalo The State University of New York

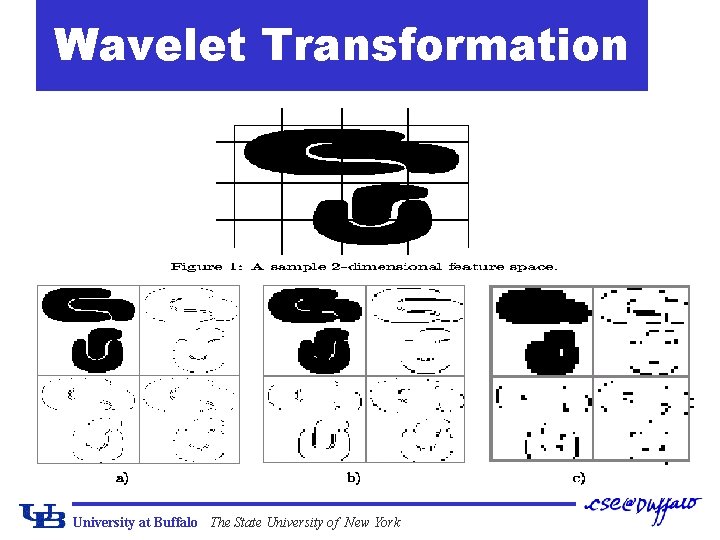
What Is Wavelet Transform? ¢Decomposes a signal into different frequency subbands q. Applicable to n-dimensional signals ¢Data are transformed to preserve relative distance between objects at different levels of resolution ¢Allow natural clusters to become more distinguishable University at Buffalo The State University of New York

Intuition Behind Using Wavelet Transform ¢ Wavelet transform filters makes clusters more distinct ¢ Effective removal of outliers ¢ Multi-resolution property of wavelet transform can help detecting clusters at different levels of accuracy ¢ Cost-efficiency University at Buffalo The State University of New York

Wavelet Transformation University at Buffalo The State University of New York

Why Is Wavelet Transform? ¢ Use hat-shape filters q Emphasize region where points cluster q Suppress weaker information in their boundaries ¢ Effective removal of outliers q Insensitive to noise, insensitive to input order ¢ Multi-resolution q Detect arbitrary shaped clusters at different scales ¢ Efficient q Complexity O(N) ¢ Only applicable to low dimensional data University at Buffalo The State University of New York

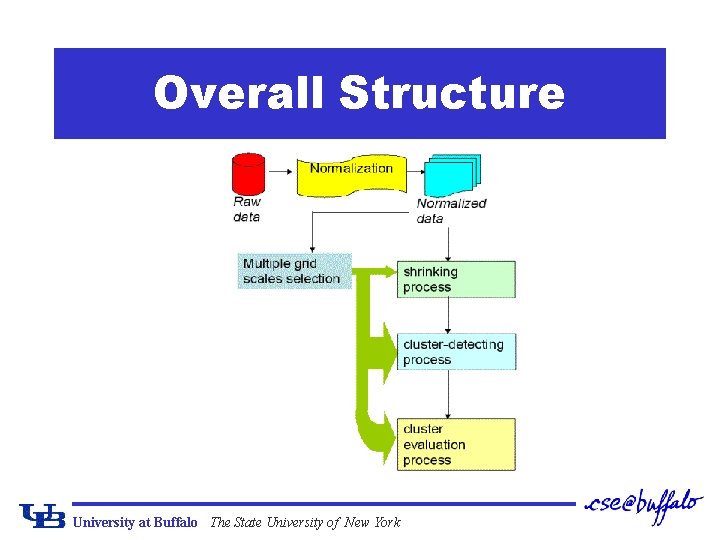
Wave. Cluster: Method ¢ Summarize the data by imposing a multidimensional grid structure on to data space q Multidimensional spatial data objects are represented in an n-dimensional feature space ¢ Apply wavelet transform on feature space to find the dense regions in the feature space ¢ Apply wavelet transform multiple times q Result in clusters at different scales from fine to coarse ¢ By Dr. Aidong Zhang’s group University at Buffalo The State University of New York

Wave. Cluster University at Buffalo The State University of New York

Shrinking: Intuition & Purpose ¢For data points in a data set, what if we could make them move towards the centroid of the natural subgroup they belong to? ¢Natural sparse subgroups become denser, thus easier to be detected; noises are further isolated. University at Buffalo The State University of New York

The Concept of Shrinking ¢ A data preprocessing technique ¢ It aims to optimize the inner structure of real data sets ¢ Each data point is “attracted” by other data points and moves to the direction in which way the attraction is the strongest ¢ Can be applied in different fields University at Buffalo The State University of New York

Data Shrinking ¢Each data point moves along the direction of the density gradient and the data set shrinks towards the inside of the clusters. ¢Points are “attracted” by their neighbors and move to create denser clusters. ¢Proceeds iteratively; repeated until the data are stabilized or the number of iterations exceeds a threshold. University at Buffalo The State University of New York

Apply shrinking into clustering field ¢Shrink the natural sparse clusters to make them much denser to facilitate further cluster-detecting process. Multiattribute hyperspace University at Buffalo The State University of New York

Overall Structure University at Buffalo The State University of New York

Data Shrinking (Cont’d) ¢ Space subdivision Normalization of data space Given the side length 1/k of grid cells, the normalized data space is subdivided into kd cells. Each grid g contains the average position (grid point) and number of data points in it. ¢ Neighboring relationship of points is grid-based. In each iteration, data points move toward the data centroid of the neighboring grids. ¢ Grid scale: q Apply different grid scales, choose best clustering results. University at Buffalo The State University of New York

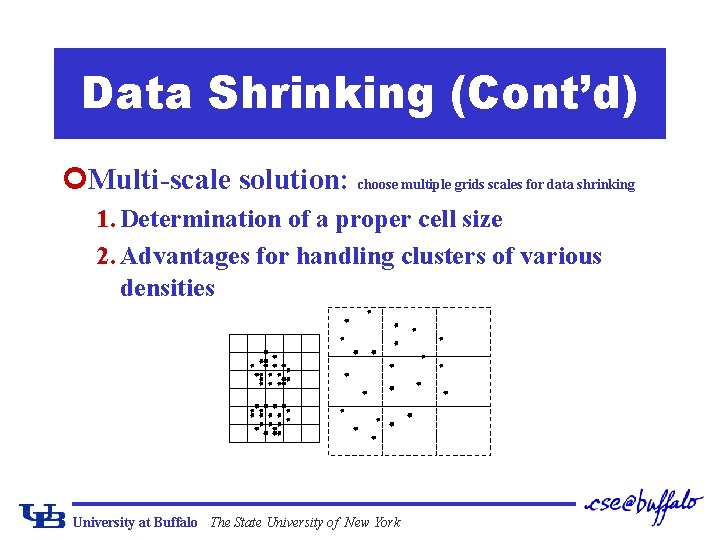
Data Shrinking (Cont’d) ¢Multi-scale solution: choose multiple grids scales for data shrinking 1. Determination of a proper cell size 2. Advantages for handling clusters of various densities University at Buffalo The State University of New York

Data Shrinking (Cont’d) ¢ Acquirement of Multi-scale A straightforward solution: use a sequence of grids of exponentially increasing cell sizes. Smin, Smin*Eg, … Smin*(Eg)ŋ = Smax, for some ŋ N Disadvantage: 1) Smin depends on the granularity of data 2) Losing important grid scale candidates University at Buffalo The State University of New York

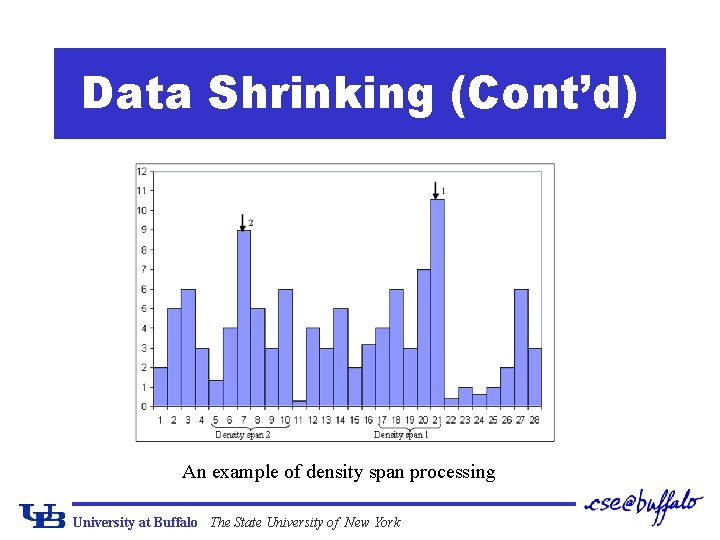
Data Shrinking (Cont’d) ¢A histogram-based approach to get reasonable grid scales q. Get histograms for dimensions: H={h 1, h 2, …, hd} q. Density span: a combination of consecutive bins’ segments on a certain dimension in which the amount of data points exceeds a threshold. q. Start from the largest bin, get density spans. q. Regard density spans with similar sizes as identical ones, and choose those with largest frequencies as grid scale candidates. University at Buffalo The State University of New York

Data Shrinking (Cont’d) An example of density span processing University at Buffalo The State University of New York

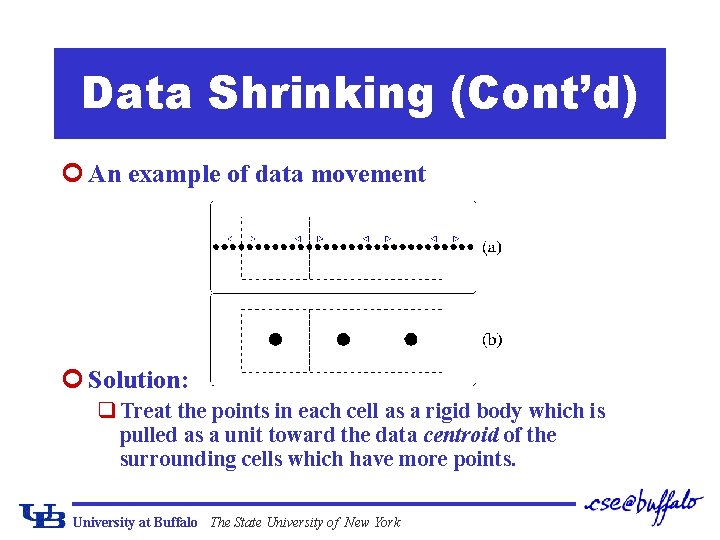
Data Shrinking (Cont’d) ¢ An example of data movement ¢ Solution: q Treat the points in each cell as a rigid body which is pulled as a unit toward the data centroid of the surrounding cells which have more points. University at Buffalo The State University of New York

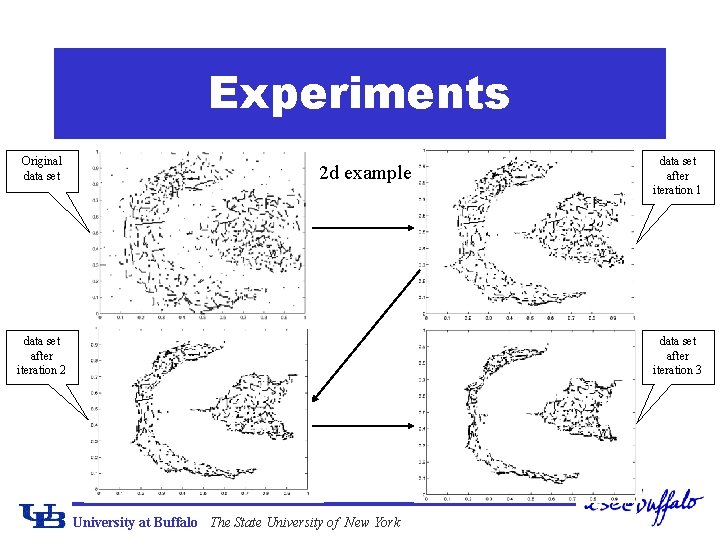
Experiments Original data set 2 d example data set after iteration 2 data set after iteration 1 data set after iteration 3 University at Buffalo The State University of New York

Cluster Detection ¢Neighboring dense cells are connected and a neighboring graph G of the dense cells is constructed. ¢Use a breadth-first search algorithm to find the components of graph G. Each component is a cluster. ¢Label data points with cluster ids. University at Buffalo The State University of New York