Watershed Based Visualization of HighDensity EEG Coherence Michael

Watershed Based Visualization of High-Density EEG Coherence Michael ten Caat 1, 2, Natasha M. Maurits 2, 3, Jos B. T. M. Roerdink 1, 2 1. Institute for Mathematics and Computing Science, University of Groningen 2. BCN Neuroimaging Center, University of Groningen 3. Department of Neurology, University Medical Center Groningen mtc@cs. rug. nl www. cs. rug. nl/~mtc ISMM, Rio de Janeiro, 10 13 October 2007

Outline • Introduction electroencephalography (EEG) coherence • Data driven visualization: – Existing: maximal clique based (MCB) – Novel: watershed based (WB) • Comparison MCB and WB • Conclusion, Discussion, Questions

EEG coherence • EEG measures electrical brain activity using up to 512 electrodes • Synchronous electrical activity between brain regions is assumed to imply functional relationships between these regions • Measure for this synchrony: EEG coherence • Coherence: similarity of a pair of signals, as a function of frequency (values between 0 and 1) • Generally computed per frequency band

Data • Participant listened to high (15%) and low (85%) tones • High tones were counted • 20 brain responses to high tones were recorded in 20 segments, using 128 EEG electrodes (high density EEG) • Significance threshold for coherence: θ = 1 p 1/(L 1) (p = probability, L = no. segments) Here, for L = 20 and p = 0. 05 : θ = 0. 15

Conventional data-driven visualization 1 3 Hz significance threshold coh > 0. 15 top 10% coh > 0. 37 top 1% coh > 0. 91 All electrodes and all significant coherences Result: visually cluttered edges

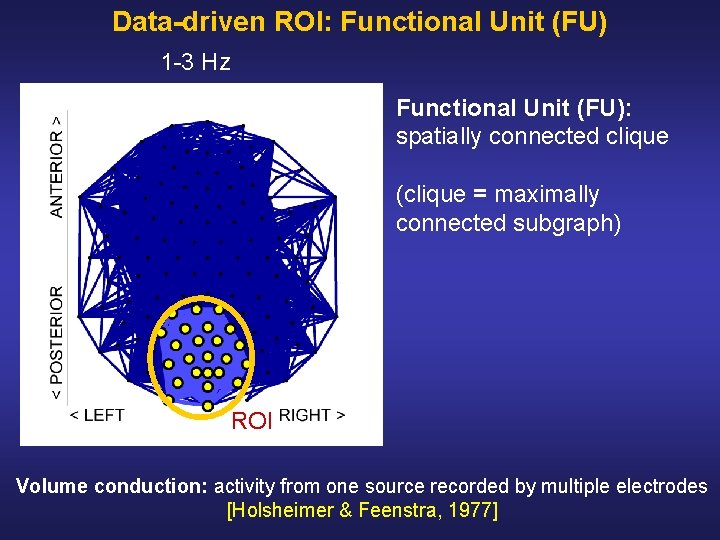
Data-driven ROI: Functional Unit (FU) 1 3 Hz Functional Unit (FU): spatially connected clique (clique = maximally connected subgraph) ROI Volume conduction: activity from one source recorded by multiple electrodes [Holsheimer & Feenstra, 1977]

Functional Unit Map • Detect functional units • Visualize functional units preserving electrode locations avoiding visual clutter

Functional Unit Map • • Detect functional units Visualize functional units preserving electrode locations avoiding visual clutter Existing maximal clique based method 1. 2. 3. 4. 5. Define neighborship electrodes Find spatially connected maximal cliques Determine functional units (FUs) Show sufficiently large FUs Visualize inter FU connections

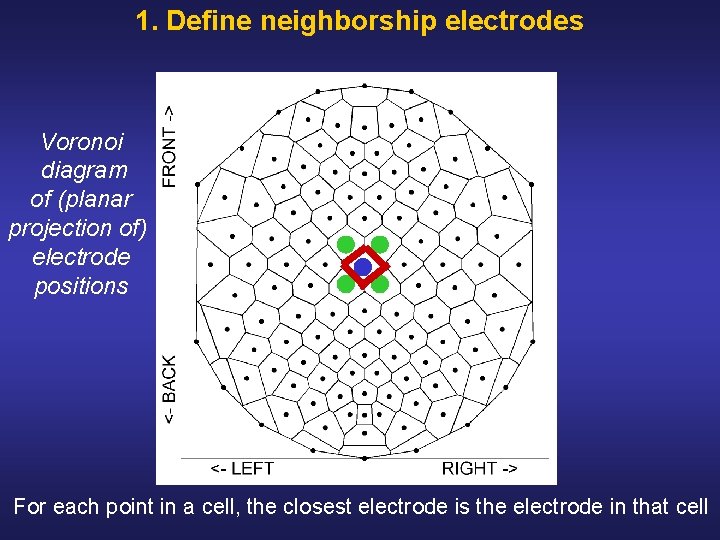
1. Define neighborship electrodes Voronoi diagram of (planar projection of) electrode positions For each point in a cell, the closest electrode is the electrode in that cell

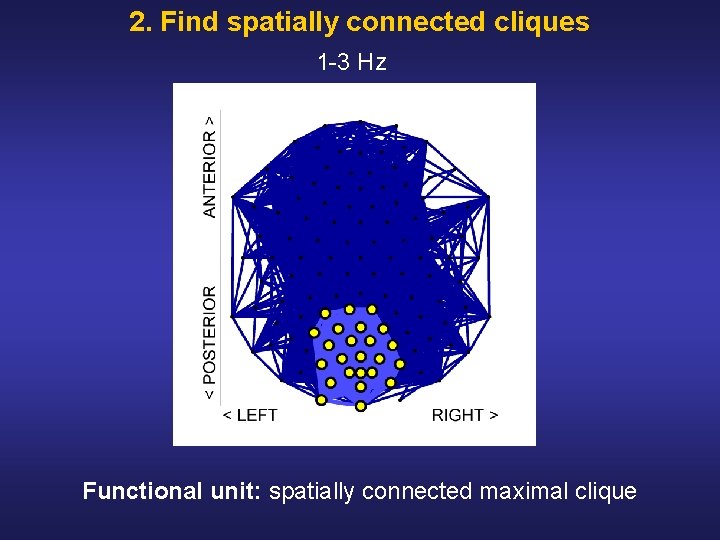
2. Find spatially connected cliques 1 3 Hz Functional unit: spatially connected maximal clique

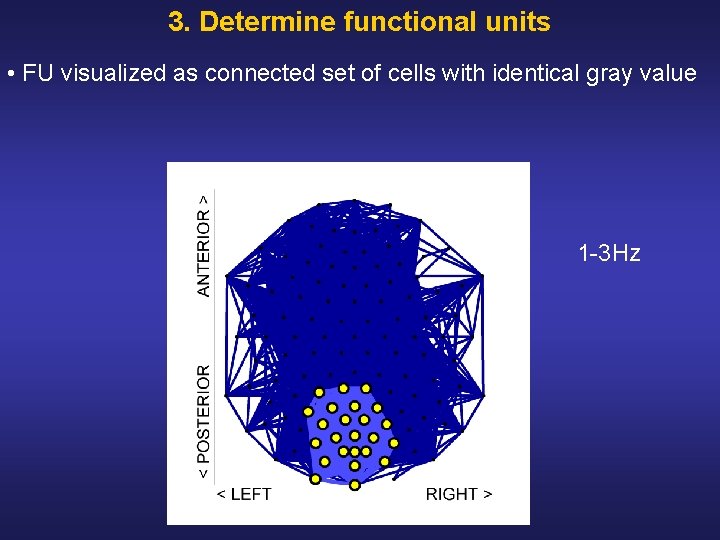
3. Determine functional units • FU visualized as connected set of cells with identical gray value 1 3 Hz

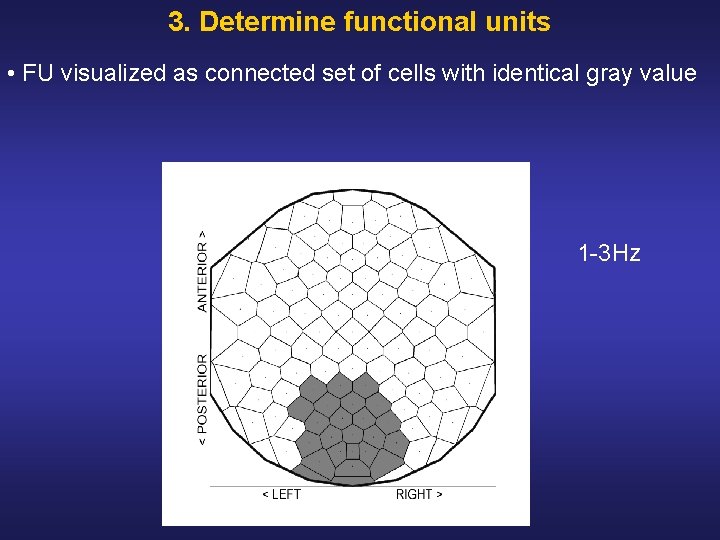
3. Determine functional units • FU visualized as connected set of cells with identical gray value 1 3 Hz

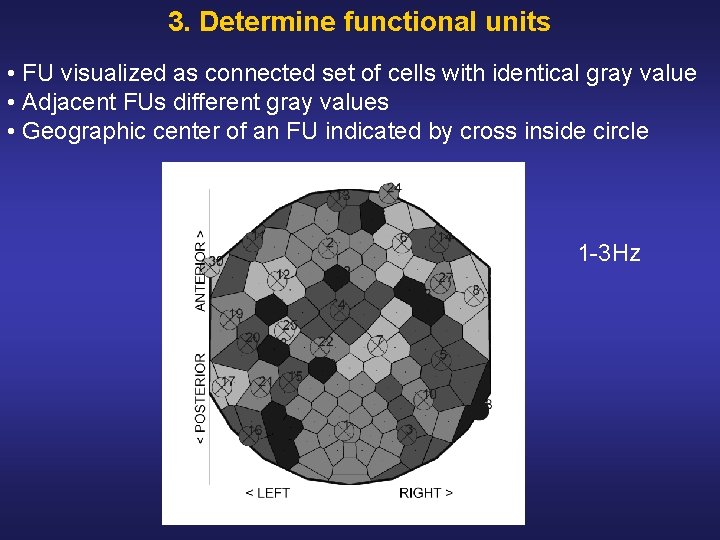
3. Determine functional units • FU visualized as connected set of cells with identical gray value • Adjacent FUs different gray values • Geographic center of an FU indicated by cross inside circle 1 3 Hz

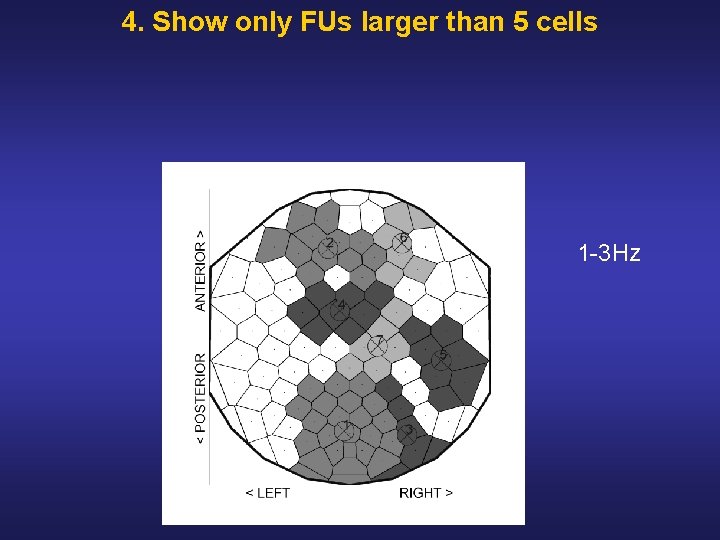
4. Show only FUs larger than 5 cells 1 3 Hz

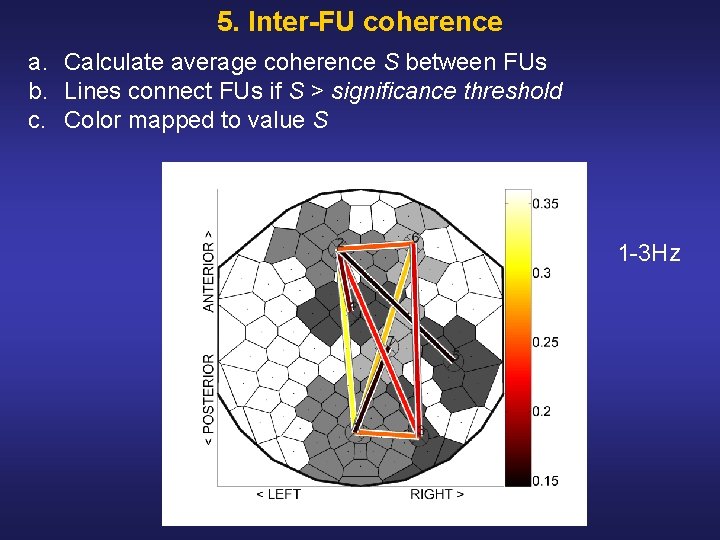
5. Inter-FU coherence a. Calculate average coherence S between FUs b. Lines connect FUs if S > significance threshold c. Color mapped to value S 1 3 Hz

Time complexity maximal clique based method: O(3 n/3), n is number of vertices (i. e. electrodes)

Goal Develop more efficient (greedy) FU detection method based on watershed transform

Watershed Based FU Maps Initialization: • Define coherence of vertex v as average coherence between v and its Voronoi neighbors • Select all local maxima as markers • Label markers and associate markers with basins • Initialize edge queues with edges between markers and their spatial neighbors (i. e. Voronoi neighbors) • Sort edges in decreasing order of value • Extend basins as follows, see: Illustration Pseudocode

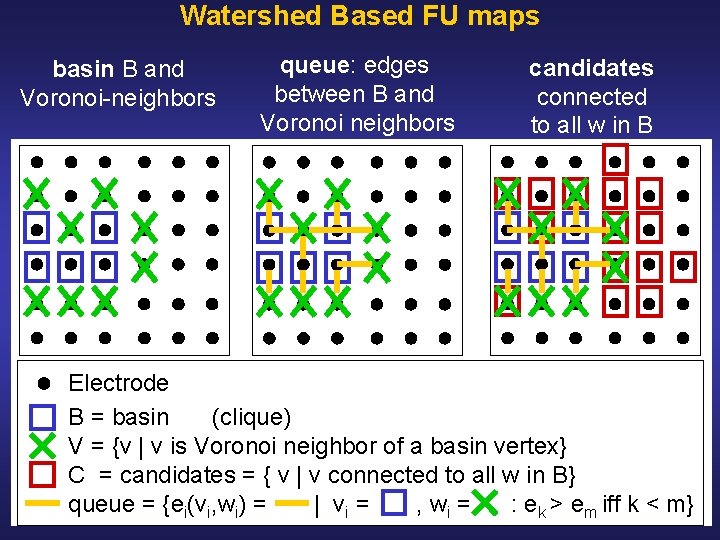
Watershed Based FU maps basin B and Voronoi neighbors queue: edges between B and Voronoi neighbors candidates connected to all w in B Electrode B = basin (clique) V = {v | v is Voronoi neighbor of a basin vertex} C = candidates = { v | v connected to all w in B} queue = {ei(vi, wi) = | vi = , wi = : ek > em iff k < m}

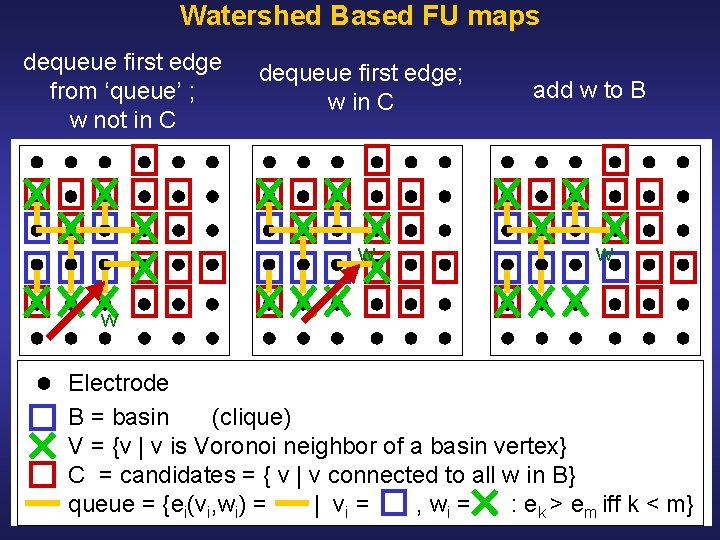
Watershed Based FU maps dequeue first edge from ‘queue’ ; w not in C dequeue first edge; w in C w add w to B w w Electrode B = basin (clique) V = {v | v is Voronoi neighbor of a basin vertex} C = candidates = { v | v connected to all w in B} queue = {ei(vi, wi) = | vi = , wi = : ek > em iff k < m}

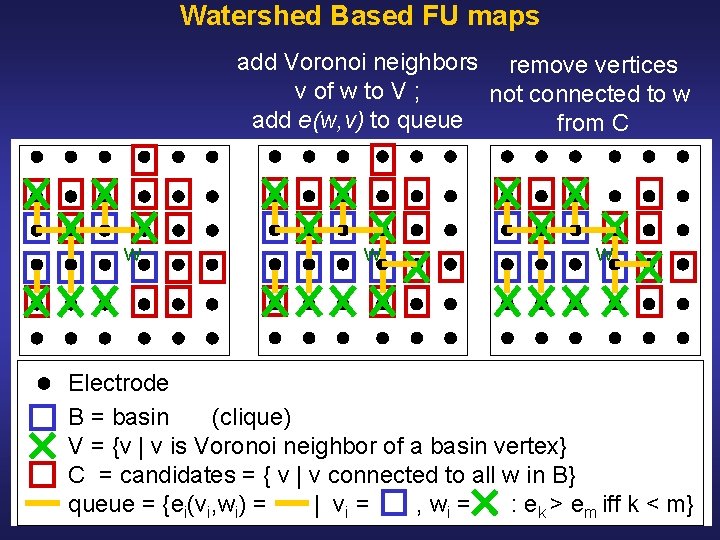
Watershed Based FU maps add Voronoi neighbors remove vertices v of w to V ; not connected to w add e(w, v) to queue from C w w w Electrode B = basin (clique) V = {v | v is Voronoi neighbor of a basin vertex} C = candidates = { v | v connected to all w in B} queue = {ei(vi, wi) = | vi = , wi = : ek > em iff k < m}

Watershed Based FU Maps 1 while queue not empty do 2 e(v, w) ← dequeue(queue) (* v in basin. L(v) *) 3 if L(w) = 0 (* w not in any basin *) 4 if w in candidates. L(v) then 5 candidates. L(v) ← intersect(candidates. L(v), adjcohw) 6 L(w) ← L(v) 7 basin. L(v) ← insert. Vertex. Sort(w, basin. L(v)) 8 for all v* in adjvorw do 9 if L(v*)=0 then insert. Edge. Sort(e(w, v*), queue) end if 10 end for 11 end if 12 end if 13 end while basin_i e(v, w) L(v) adjcohw adjvorw queue vertices in basin (sorted by vertex nr) edge between vertex v and w basin label of vertex v vertices adjacent to w in the coherence graph (sorted by nr) Voronoi neighbors of w (sorted by nr) list of edges sorted in decreasing order; e(v, w) is added v is put into a basin for every unlabeled Voronoi neighbor w of v

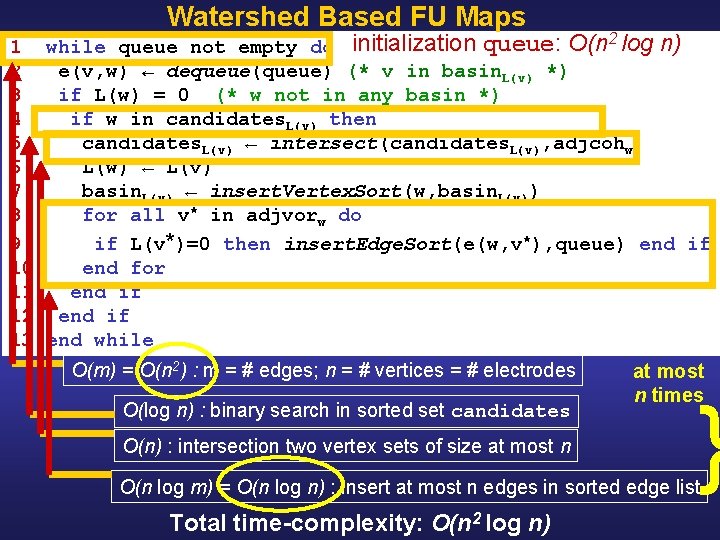
Watershed Based FU Maps 1 while queue not empty do initialization queue: O(n 2 log n) 2 e(v, w) ← dequeue(queue) (* v in basin. L(v) *) 3 if L(w) = 0 (* w not in any basin *) 4 if w in candidates. L(v) then 5 candidates. L(v) ← intersect(candidates. L(v), adjcohw) 6 L(w) ← L(v) 7 basin. L(v) ← insert. Vertex. Sort(w, basin. L(v)) 8 for all v* in adjvorw do 9 if L(v*)=0 then insert. Edge. Sort(e(w, v*), queue) end if 10 end for 11 end if 12 end if 13 end while O(m) = O(n 2) : m = # edges; n = # vertices = # electrodes O(log n) : binary search in sorted set candidates O(n) : intersection two vertex sets of size at most n times } O(n log m) = O(n log n) : insert at most n edges in sorted edge list Total time-complexity: O(n 2 log n)

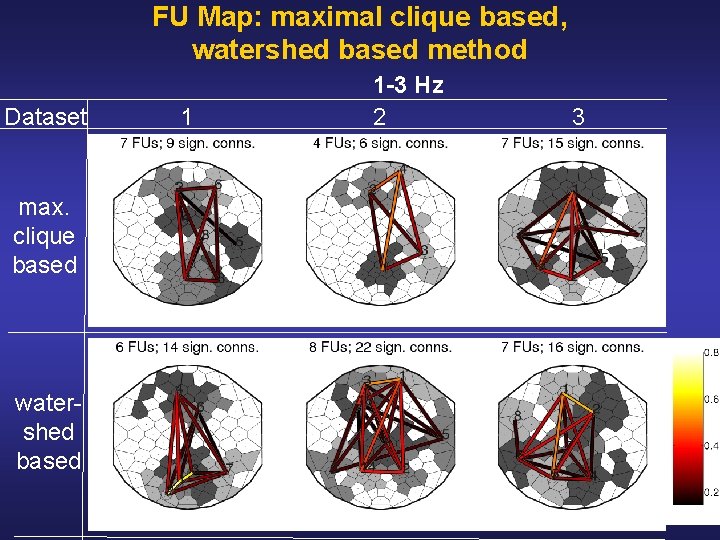
FU Map: maximal clique based, watershed based method Dataset max. clique based water shed based 1 1 -3 Hz 2 3

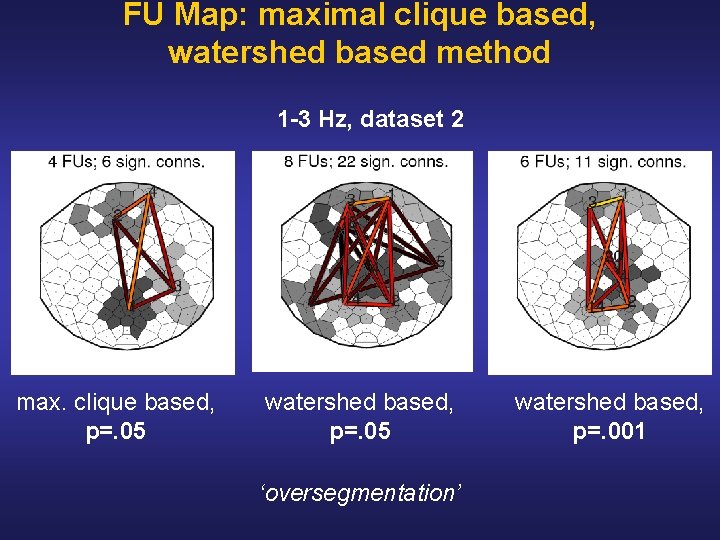
FU Map: maximal clique based, watershed based method 1 -3 Hz, dataset 2 max. clique based, p=. 05 watershed based, p=. 05 ‘oversegmentation’ watershed based, p=. 001

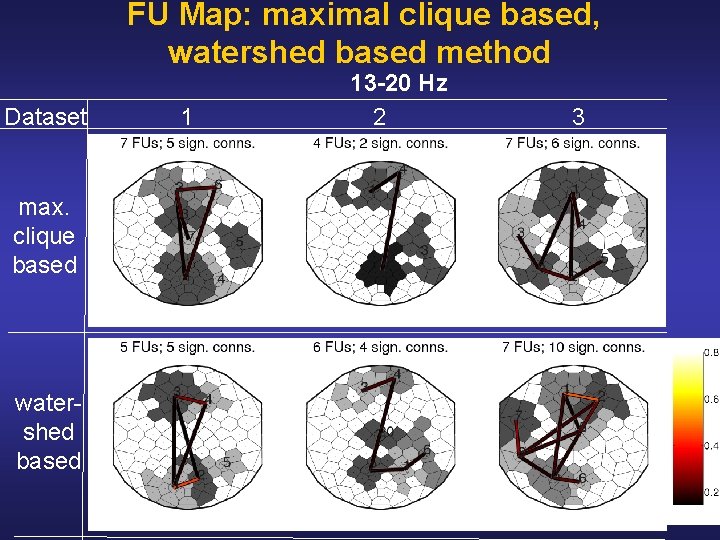
FU Map: maximal clique based, watershed based method Dataset max. clique based water shed based 1 13 -20 Hz 2 3

Interpretation Results • Simultaneous activity at a more global scale for a lower EEG frequency at a more local scale for a higher EEG frequency [Nunez et al, Electroenceph Clin Neurophysiol 103, 5 (1997)] In accordance, we observe less inter FU connections for higher frequencies • Connections between anterior and posterior FUs are probably associated with the two most important sources of activity for this type of data [Comerchero & Polich, Clin Neurophysiol 110, 1 (1999)] Correspondingly, we observe connections between anterior and posterior FUs

Performance maximal clique based and watershed based method Method Time complexity Avg. FU detection time Maximal clique based O(3 n/3) 24 s Watershed based O(n 2 log n) 0. 06 s n = no. electrodes (up to 512) Average speedup: 400 x

Conclusion & Discussion • Functional unit (FU) map FU = data driven ROI = spatially connected clique data driven EEG coherence visualization • FU detection Existing method § Maximal clique based (MCB) § Time complexity O(3 n/3) Novel method § Watershed based (WB) § Time complexity O(n 2 log n) • Result: WB method on average 400 x faster than MCB method FU maps: MCB and WB similar, but • Oversegmentation: adapting significance threshold increases similarity future: merge spatially neighboring FUs if together one FU

Future Work • Case studies: aging, mental fatigue • Group analysis