Water Research Laboratory School of Civil Environmental Engineering

Water Research Laboratory | School of Civil & Environmental Engineering Considerations for the Design of Rock Armoured Coastal Protection on Fringing Reef Coastlines Matt Blacka, Kristen Splinter, Rebecca Killalea

Outline Problem Thoughts Modelling More thoughts Conclusions (kind of)

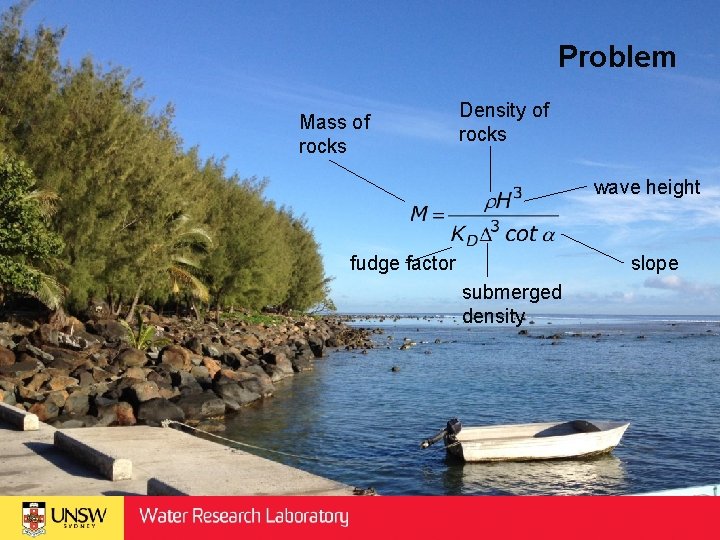
Problem Mass of rocks Density of rocks wave height slope fudge factor submerged density

Problem Hudson equation established & verified for non-fringing reef environments How do we work out H -

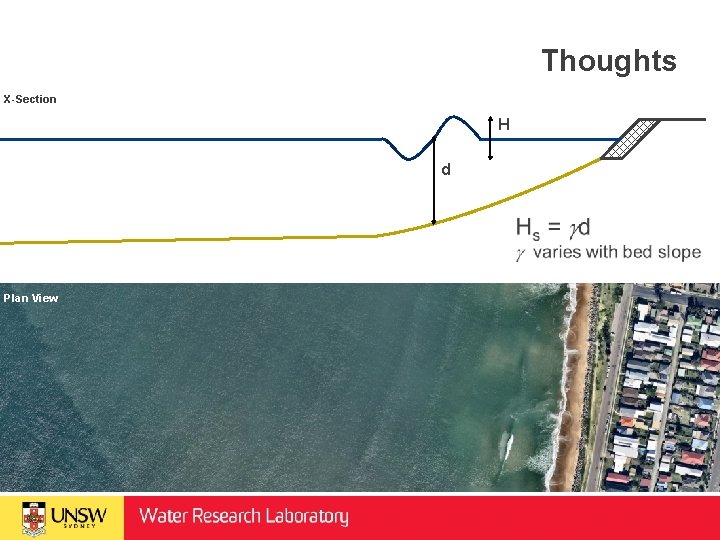
Thoughts X-Section H d Plan View

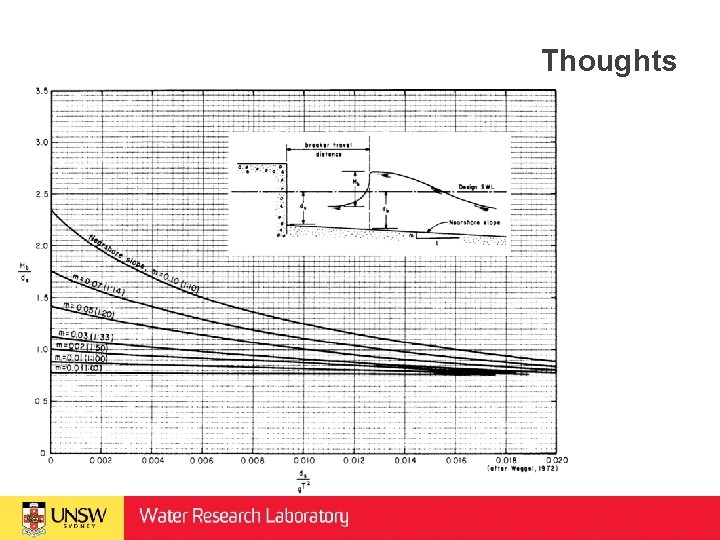
Thoughts

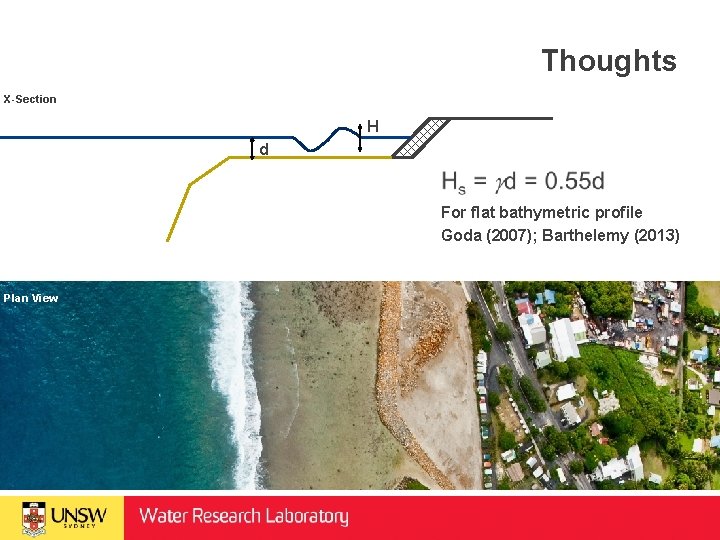
Thoughts X-Section H d For flat bathymetric profile Goda (2007); Barthelemy (2013) Plan View

Modelling • 2 D scale physical model testing program in wave flume • Undertaken to investigate: 1. Are coastal protection rock sizes predicted using depth limed design wave height and Hudson equation acceptable for reef fringed locations? 2. Even if we use more accurately predicted wave heights with Hudson equation, is the equation able to accurately predict the required armour rock sizes?

Modelling • 2 D scale physical model testing program in wave flume • 44 m long, 1. 2 m wide, 1. 8 m deep wave channel

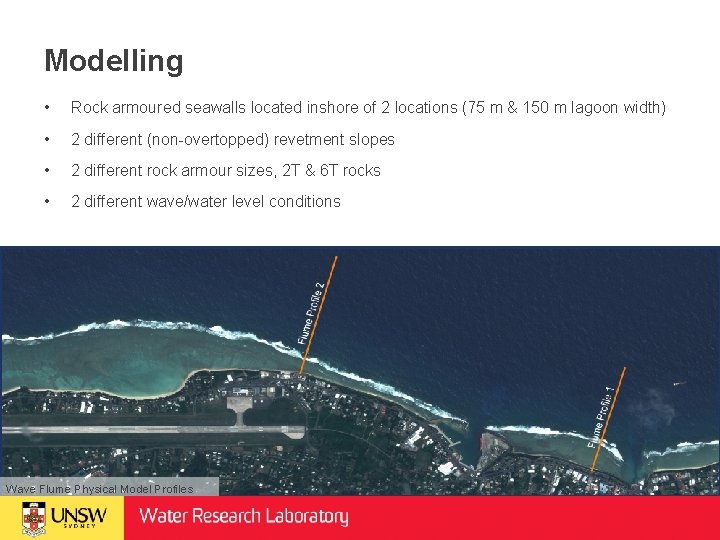
Modelling • Rock armoured seawalls located inshore of 2 locations (75 m & 150 m lagoon width) • 2 different (non-overtopped) revetment slopes • 2 different rock armour sizes, 2 T & 6 T rocks • 2 different wave/water level conditions Wave Flume Physical Model Profiles

Modelling - Results • Initial desktop predictions using Hudson equation and assuming simplistic depth limited waves suggested: • For smaller wave condition, rocks as small as 0. 5 T should have been adequate • For larger wave condition, rocks of the order of 2 T should have been adequate • Scale physical model tests indicated that for the smaller wave condition: • 2 T armouring suffered minor damage, 6 T armouring insignificant damage • Scale physical model tests indicated that for the larger wave condition: • with narrow reef width, 2 T armouring failed, 6 T armouring adequate but minor damage • With wide reef width both 2 T and 6 T adequate but minor damage • General conclusion is that required rock armour size is under-predicted by Hudson equation and simplistic depth-limited wave height calculation, especially for narrow lagoon widths

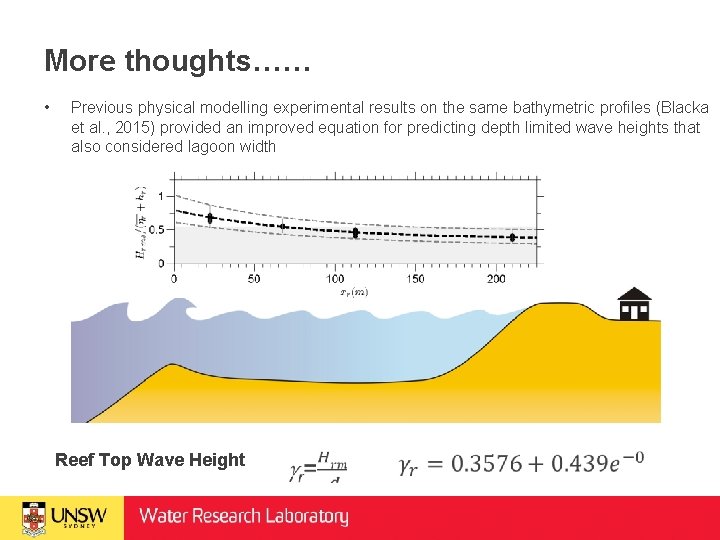
More thoughts…… • Previous physical modelling experimental results on the same bathymetric profiles (Blacka et al. , 2015) provided an improved equation for predicting depth limited wave heights that also considered lagoon width Reef Top Wave Height

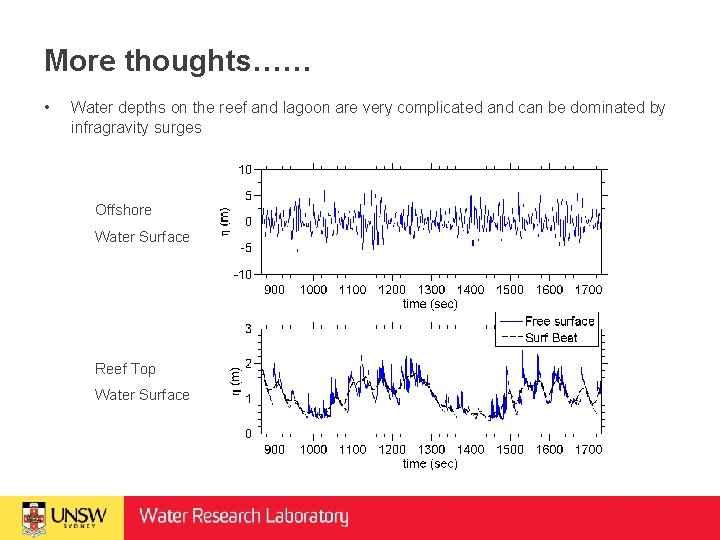
More thoughts…… • Water depths on the reef and lagoon are very complicated and can be dominated by infragravity surges Offshore Water Surface Reef Top Water Surface

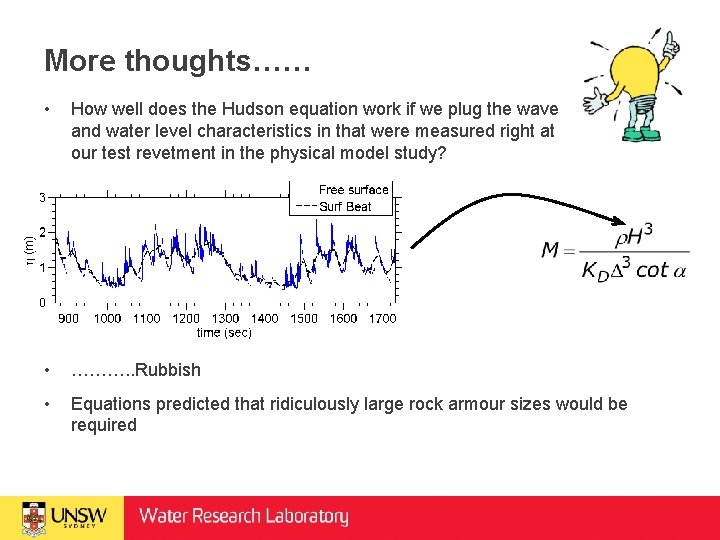
More thoughts…… • How well does the Hudson equation work if we plug the wave and water level characteristics in that were measured right at our test revetment in the physical model study? • ………. . Rubbish • Equations predicted that ridiculously large rock armour sizes would be required

Conclusions (kind of) • Existing equations for design of rock armour on coastal protection structures were not developed or intended for use in locations with fringing coral reefs • If these equations are going to be used for locations with a fringing reef, additional effort needs to go in to considering: • The width of reef/lagoon and its impact on wave heights at the seawall • The impact of long period infragravity surges on water levels • Even if you predict the environmental design conditions well, the available armour sizing equations are not particularly accurate • Ongoing physical modelling is required to refine: • Exactly which wave parameters we should be feeding into the equation • Better values for the Kd fudge factor that improve the equation for reef fringed locations

Questions?