Wastewater Treatment modeling an integrated system Improving efficiency

Wastewater Treatment: modeling an integrated system Improving efficiency of wastewater treatment plants Tess Scanlon

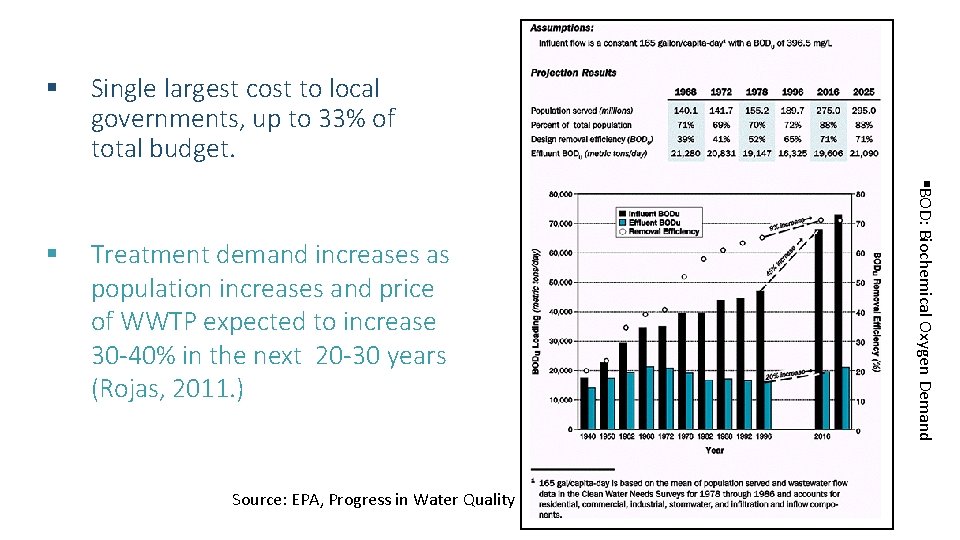
Single largest cost to local governments, up to 33% of total budget. § Treatment demand increases as population increases and price of WWTP expected to increase 30 -40% in the next 20 -30 years (Rojas, 2011. ) Source: EPA, Progress in Water Quality §BOD: Biochemical Oxygen Demand §

Problem: § Conventional WWTP and corresponding models use activated sludge treatment ponds § These methods/models are inadequate § The activated sludge models represent lowest std for treatment at highest cost Modeling for better management: § As demand increases, so must process efficiency § Wastewater treatment should be viewed as an integrated system yielding byproducts that can be reused in throughout the cycle

Municipal Wastewater Treatment Plants § Phase 1: Physical Filtration § Phase 2: Primary Treatment sedimentation and microbial oxidation § Separates influent from heavy insoluble materials § Microbial oxidation decomposes organic contaminates and produces CO 2

Municipal Wastewater Treatment Plants § Phase 3: Algal production and harvest § Utilizes nutrients (N and P) for biomass growth § Produces O 2 § Fixes CO 2 § Adsorbs heavy metals and organic contaminates § Biomass conversion into energy § Phase 4: Land Application § Uses treated effluent to irrigate tree plantation or other non-agricultural land using nutrient rich treated effluent

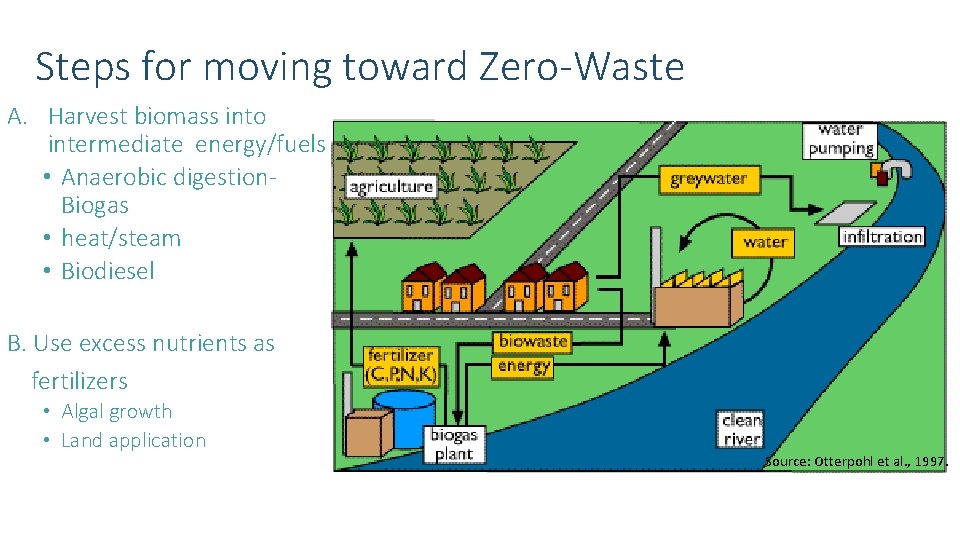
Steps for moving toward Zero-Waste A. Harvest biomass into intermediate energy/fuels • Anaerobic digestion. Biogas • heat/steam • Biodiesel B. Use excess nutrients as fertilizers • Algal growth • Land application Source: Otterpohl et al. , 1997.

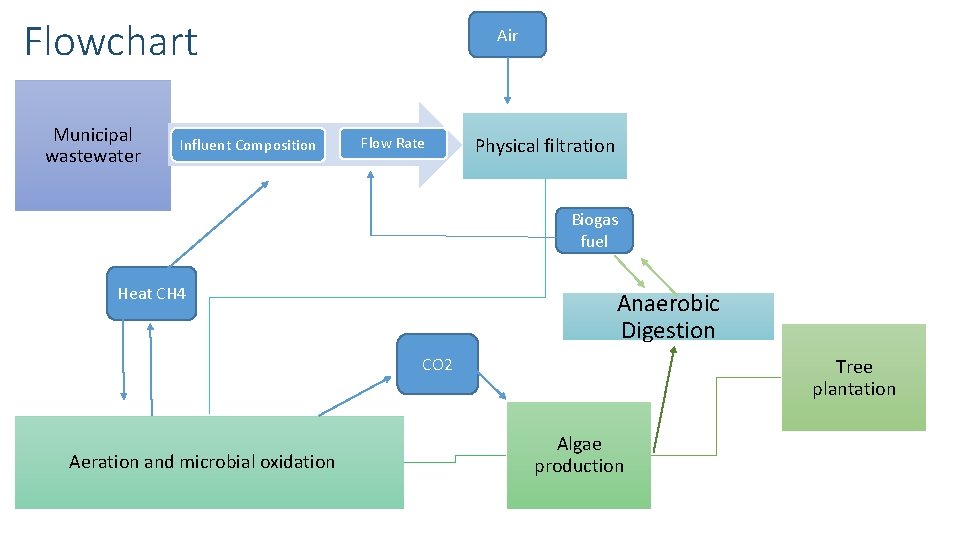
Flowchart Municipal wastewater Influent Composition Air Flow Rate Physical filtration Biogas fuel Heat CH 4 Anaerobic Digestion CO 2 Aeration and microbial oxidation Tree plantation Algae production

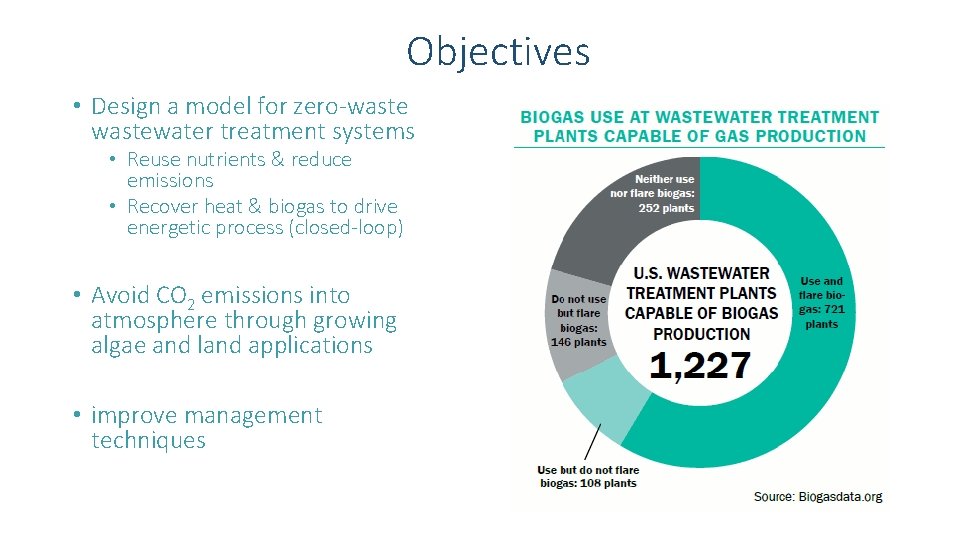
Objectives • Design a model for zero-wastewater treatment systems • Reuse nutrients & reduce emissions • Recover heat & biogas to drive energetic process (closed-loop) • Avoid CO 2 emissions into atmosphere through growing algae and land applications • improve management techniques

Domain • Deterministic steady-state model. Monthly time-step System Modules: A. B. C. D. E. Hydraulics Treatments: Filtration, Sedimentation, Microbial oxidation Algae Production Kinetics Anaerobic Digester Kinetics Land application: Tree Plantation Input parameters gives user option to optimize process and/or product variables Lets the user determine case-by-case settings that produces highest yield for byproduct that is most economically profitable

Assumptions • Treatment occurs at constant temperature 10 - 25*C • Treatment occurs at p. H 7. 5 • Biomass influent is homogenous, so contamination biodegradation occurs at constant rate • N, P, and other inorganic molecules are not limiting for biomass growth • Assumptions exist for retention time limits in tanks. Averages formation and settling time and are used to assume proper effluent results • Organic contaminates known

Major Module Inputs A. Hydraulic Process: flow rates tank volumes B. Treatment process: Energy (WKh/m 3) influent/effluent compositions (mg/l) tank retention time (days) C. Algae growth: light absorption CO 2 Nutrients algae strains organic contaminates decay rates =algal growth rates D. Harvesting algae Energy (WKh/m 3) E. Land application: light absorption precipitation and irrigation rate growth partitioning Stand size

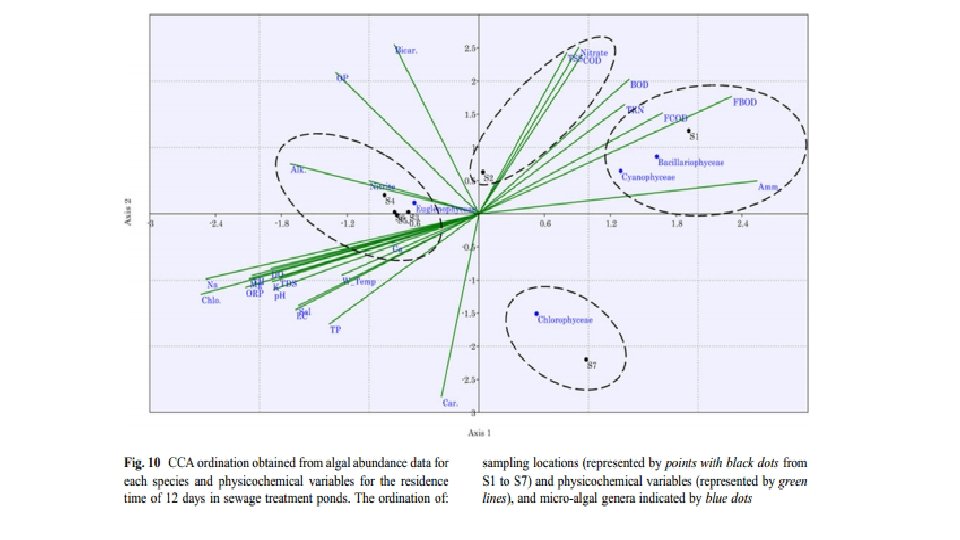
A further thought for inputs in algal growth Park et al. , 2011

Major Outputs • P and N 2 (used during algae growth) • CO 2 (used during algae growth) • Biogas (captured) • Heat (captured) • CH 4 (also reusable as input) • Biomass slurry • Treated wastewater for Irrigation • Poplar growth for harvest

Model testing and implementation • Process optimization makes it difficult model dynamic processes. • A lot of research modeling chemical processes differ in their approach • Deterministic or stochastic/dynamic? • Offset as much energy as possible through maximizing algae harvest for biofuels • Room for Further Investigation: Optimizing algal growth • High energy for biogas/fuel = high lipid concentration • Algal growth takes up lots of land b/c of required surface area for photosynthesis

Lesson: models assess show the (potential) effects of the whole system not individual steps Friedrich et al. , 2009

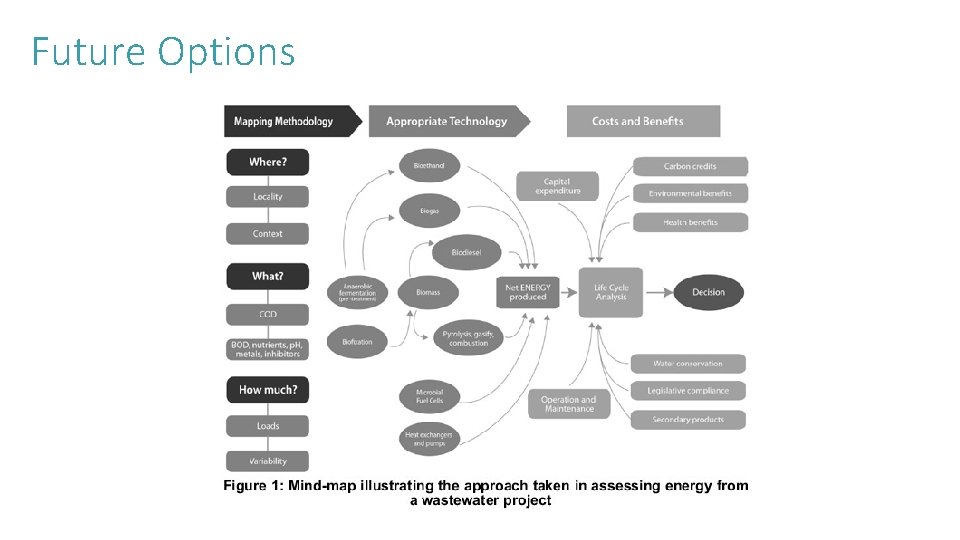
Future Options