Warmup This table shows a persons reported income
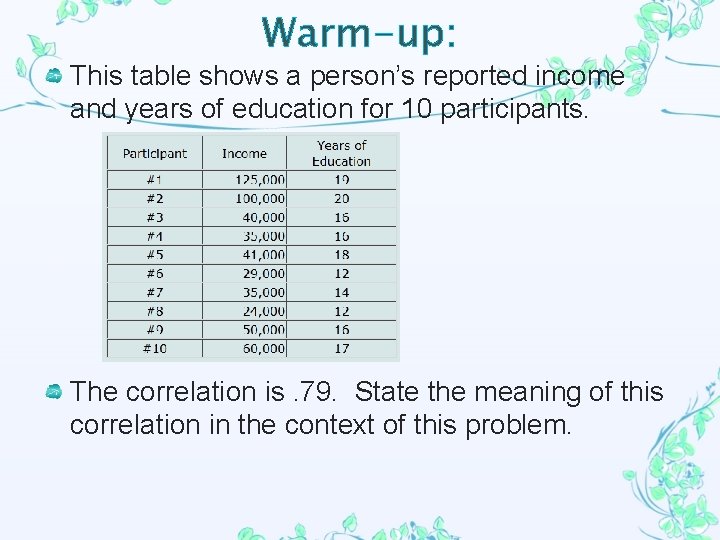
Warm-up: This table shows a person’s reported income and years of education for 10 participants. The correlation is. 79. State the meaning of this correlation in the context of this problem.

Chapter 3. 2 Linear Regression R 2 and Residuals

Least-Squares Regression Line The LSRL is a model used to represent a set of quantitative data. Suppose you find the distance from each point in the data to the linear model, then square those distances and find the sum. This is called the sum of the squares of the residuals. The Least-Squares Regression Line (LSRL) is the line that minimizes this sum. The equation of the LSRL is
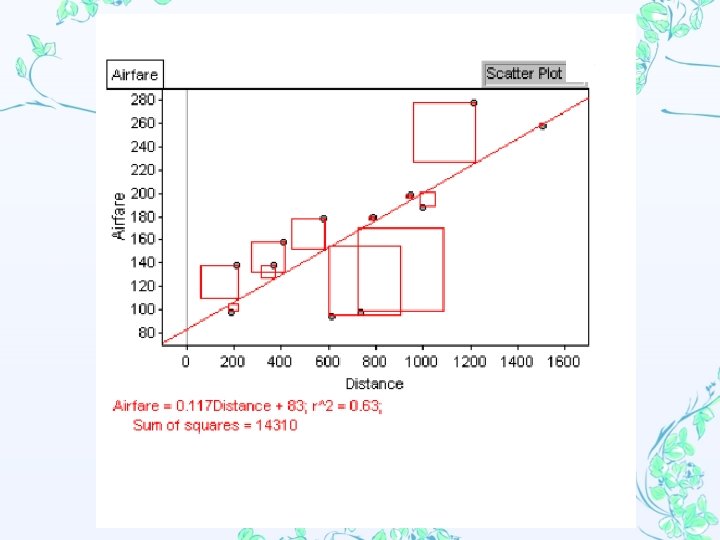

x represents explanatory variable (actual data). represents predicted y-value. b 0 represents y-intercept. b 1 represents slope.

Given a set of data, you can calculate the LSRL (without using your calculator!). Knowing the correlation makes this task even easier. Use the following formulas: Also, note that:

Exercise 1: The correlation (r) between the number of wins by American League baseball teams and the average attendance at their home games for the 2006 season is 0. 696. a) What would you predict about the Average Attendance for a team that is 2 standard deviations above average in wins? The average attendance will be (0. 696)(2) = 1. 392 standard deviations above average.

b) If a team is 1 standard deviation below average in attendance, what would you predict about the number of games the team has won? The number of games the team has won will be (0. 696)(1) = 0. 696 standard deviations below the average wins. Exercise 2: Find the LSRL given the summary statistics – Tale of 2 Regressions WKS

Coefficient of Determination The coefficient of determination, also called R 2, is the square of the r-value (correlation). The R 2 value tells how much of the variation in the response variable is accounted for by the linear regression model. For example, if R 2 = 1, then 100% of the variability in the response variable is accounted for by the linear model. In other words, the relationship between the two variables is perfectly linear. If R 2 = 0. 95, we can conclude that 95 % of the variability in the response variable is accounted for by the linear relationship with the explanatory variable.

Understanding r-squared: a single point simplification Al Coons Buckingham Browne & Nichols School Cambridge, MA Adapted to Peck, Olsen, Devore by Lee Kucera Capistrano Valley High School Mission Viejo, CA
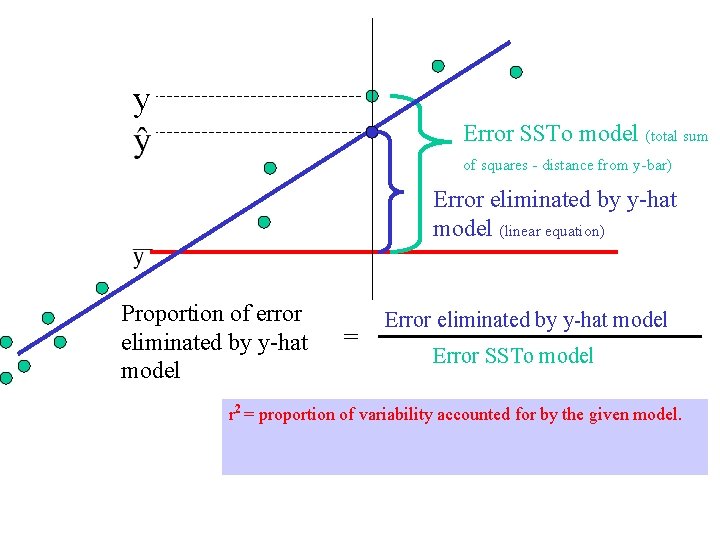
y Error SSTo model (total sum of squares - distance from y-bar) Error eliminated by y-hat model (linear equation) Proportion of error eliminated by y-hat model = Error eliminated by y-hat model Error SSTo model r 2 = proportion of variability accounted for by the given model.
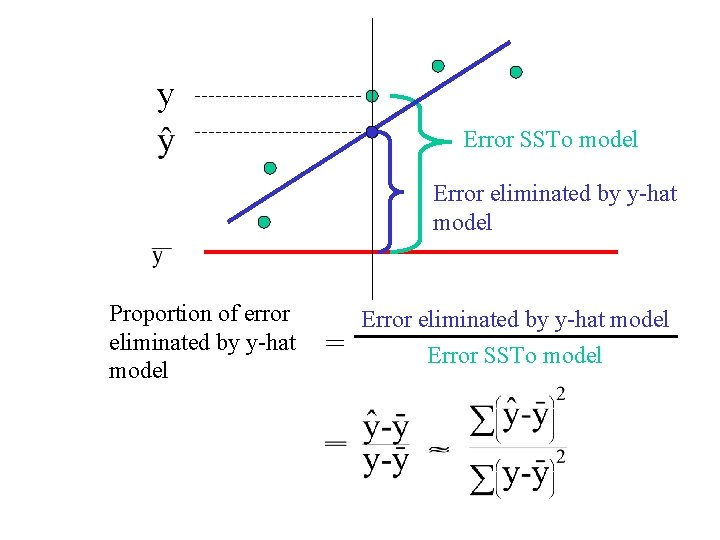
y Error SSTo model Error eliminated by y-hat model Proportion of error eliminated by y-hat model = Error eliminated by y-hat model Error SSTo model
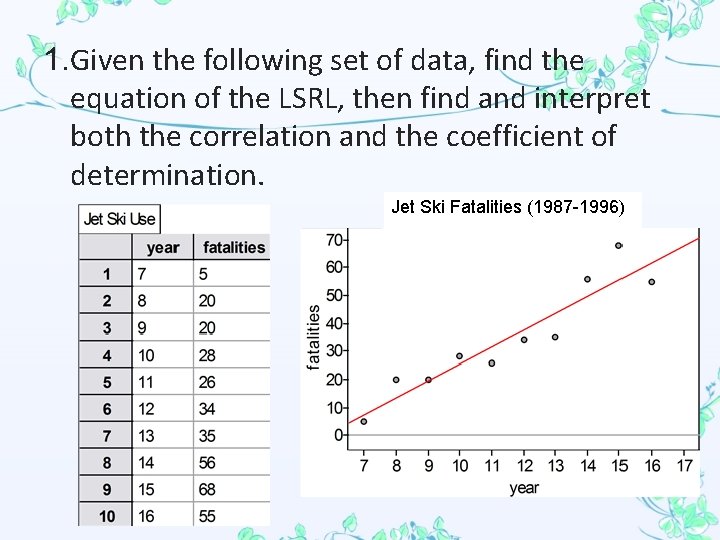
1. Given the following set of data, find the equation of the LSRL, then find and interpret both the correlation and the coefficient of determination. Jet Ski Fatalities (1987 -1996)

a. LSRL: fatal = -34. 648 + 6. 03 (year) (use meaningful variables in your equation rather than x and y, and use proper statistical notation!) b. Correlation (r-value): 0. 938. A correlation of 0. 938 indicates that there is a strong, positive, linear relationship between year and number of fatalities. c. Coefficient of determination (R 2): 0. 880. An R 2 value of 0. 880 indicates that 88% of the variability in number of fatalities is accounted for by the linear relationship with the year. d. Give the meaning of the slope. Each year, the model predicts that the # of fatalities increases by 6. 03 on average.

NOTE: Go over the meaning of slope in the context of the problem. Also explain the formula for the slope ( by showing the Understanding r ppt. )

Understanding the Formula slope = r (Sy/Sx) Al Coons Buckingham Browne & Nichols School Cambridge, MA al_coons@bbns. org
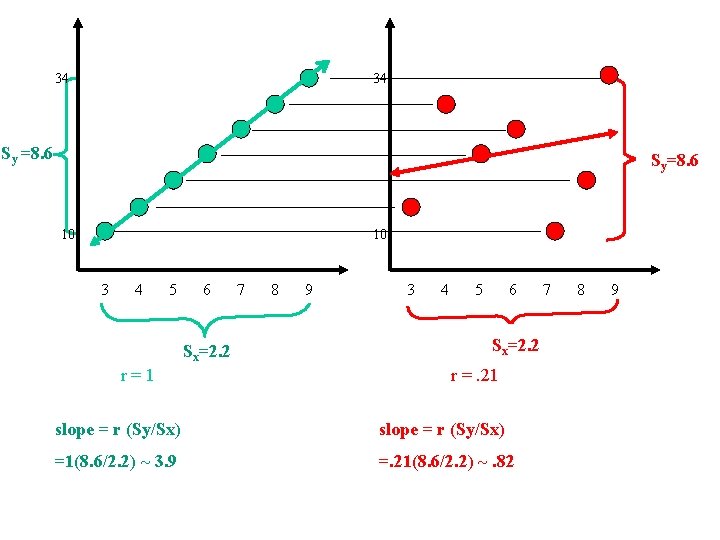
34 34 Sy =8. 6 =? Syy=8. 6 10 10 3 4 5 6 Sx=2. 2 r =r ? = 1 7 8 9 3 4 5 6 x=? SSx=2. 2 r =. 21 ? slope = r (Sy/Sx) =1(8. 6/2. 2) ~ 3. 9 =. 21(8. 6/2. 2) ~. 82 7 8 9

1. A study of class attendance and grades earned among first-year students at a state university showed that in general students who attended a higher percent of their classes earned higher grades. Class attendance explained 16% of the variation in grades among the students. What is the numerical correlation between percent of classes attended and grades earned? 0. 4 * Check if r > 0 or r < 0.

Residual Plots A residual is the difference between the observed y-value and the predicted y-value for a given x-value. residual =

The sum of the squares of the residuals (SSR) is used to determine the Least-Squares Regression Line for a given set of data. A residual plot is a scatterplot which graphs the residuals on the vertical axis and the values of the explanatory variable on the horizontal axis for each data point, .

The residual plot gives a visual representation of the amount of error in the model. The closer the residuals are to zero, the smaller the error and the more accurate the model. The LSRL is a good model if the residual plot shows random scatter relatively close to the horizontal axis (zero). The horizontal axis represents the LSRL.

Points in the residual plot that lie directly on the horizontal axis lie directly on the LSRL. Points in the residual plot that lie above the horizontal axis lie above the LSRL. Therefore, the model gives an underestimate at that point. Therefore positive residuals represent underestimates. Points in the residual plot that lie below the horizontal axis, lie below the LSRL. Therefore the model gives an overestimate at that point. Therefore negative residuals represent overestimates. The LSRL is not a good model if the residual plot shows a pattern.

3. Construct a well-labeled residual plot using the data on jet ski fatalities from #1. What can you conclude about the appropriateness of the linear model based on the residual plot?
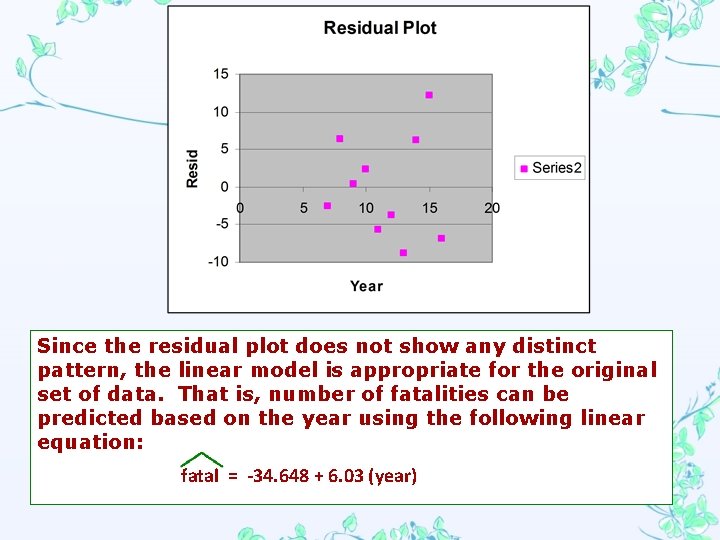
Since the residual plot does not show any distinct pattern, the linear model is appropriate for the original set of data. That is, number of fatalities can be predicted based on the year using the following linear equation: fatal = -34. 648 + 6. 03 (year)
- Slides: 24