Warmup m Evaluate a b c d for

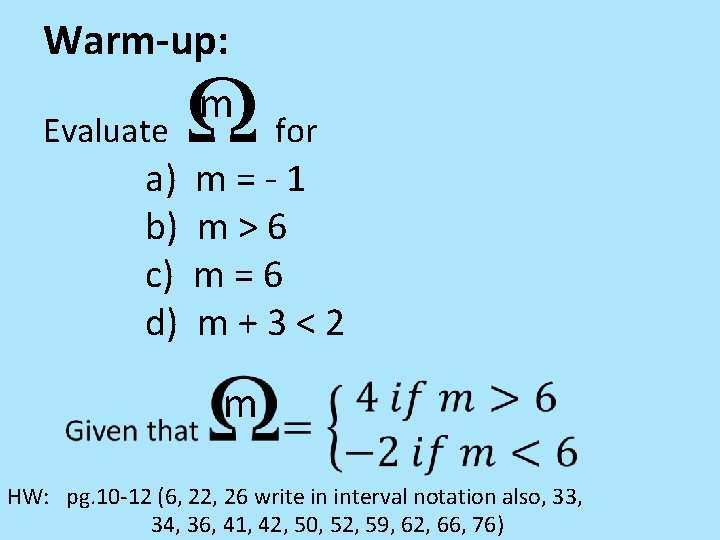
Warm-up: m Evaluate a) b) c) d) for m=-1 m>6 m=6 m+3<2 m HW: pg. 10 -12 (6, 22, 26 write in interval notation also, 33, 34, 36, 41, 42, 50, 52, 59, 62, 66, 76)

P. 1: Real Numbers Objective: • Classify real numbers • Order real numbers and use inequalities • Interpret and represent bounded and unbounded inequalities in words and in symbols. • Evaluate absolute values • Know the basic rules of algebra

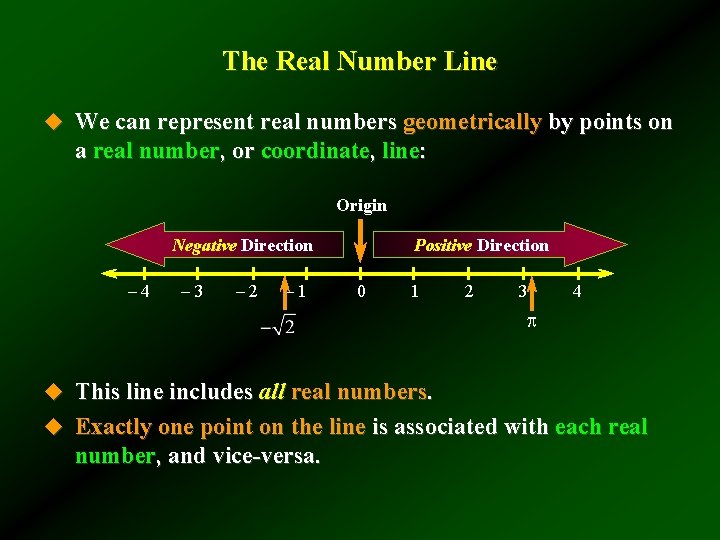
The Real Number Line u We can represent real numbers geometrically by points on a real number, or coordinate, line: Origin Negative Direction – 4 – 3 – 2 – 1 Positive Direction 0 1 2 3 4 u This line includes all real numbers. u Exactly one point on the line is associated with each real number, and vice-versa.

Real Numbers: numbers used in every day life. Ex) -5, 9, 0, , Subsets of real numbers: Natural {1, 2, 3, 4…} Whole numbers {0, 1, 2, 3, 4, …} Integers {…, -3, -2, -1, 0, 1, 2, 3, …}

Rational Numbers a number is rational if it can be written as a ratio of two integers such that the denominator is not zero. The decimal portion of a rational number either… – repeats – terminates

Irrational Number a real number that cannot be written as a ratio of two integers. The decimal portion of an irrational number is …. – infinite and nonrepeating

Ex) Determine which numbers in the set are (a)natural, (b)whole numbers, (c)integers, (d) rational, (e) irrational. Then plot them on the real number line. -1 3. 6 125/111 2 4. 132132…

Finite Intervals Open Intervals • The set of real numbers that lie strictly between two fixed numbers a and b is called an open interval (a, b). • It consists of all the real numbers that satisfy the inequalities a < x < b. • It is called “open” because neither of its endpoints are included in the interval.

Finite Intervals Closed Intervals • The set of real numbers that lie between two fixed numbers a and b, that includes a and b, is called a closed interval [a, b]. • It consists of all the real numbers that satisfy the inequalities a x b. • It is called “closed” because both of its endpoints are included in the interval.

Finite Intervals Half-Open Intervals • The set of real numbers between two fixed numbers a and b, that contains only one of its endpoints a or b, is called a half-open interval (a, b] or [a, b). • It consists of all the real numbers that satisfy the inequalities a < x b or a x < b.

Infinite Intervals Examples of infinite intervals include: • (a, ), [a, ), (– , a), and (– , a]. • The above are defined, respectively, by the set of real numbers that satisfy x > a, x < a, x a.

Interpreting Inequalities Bounded and Unbounded Intervals on the Real Number Line: Notation [a, b] (a, b) [a, b) (- , b) Interval Type Inequality Graph

Ex) Use inequality notation to describe each of the following: a. C is at most -3 b. [-1, 4)

Ex) Give a verbal description of each interval a. (-2, 3) b. (- , 5] Ex) Write in interval notation. a. m > 6 b. 3 < k ≤ 8

Absolute Value u The absolute value of a number a is denoted |a| and is defined by

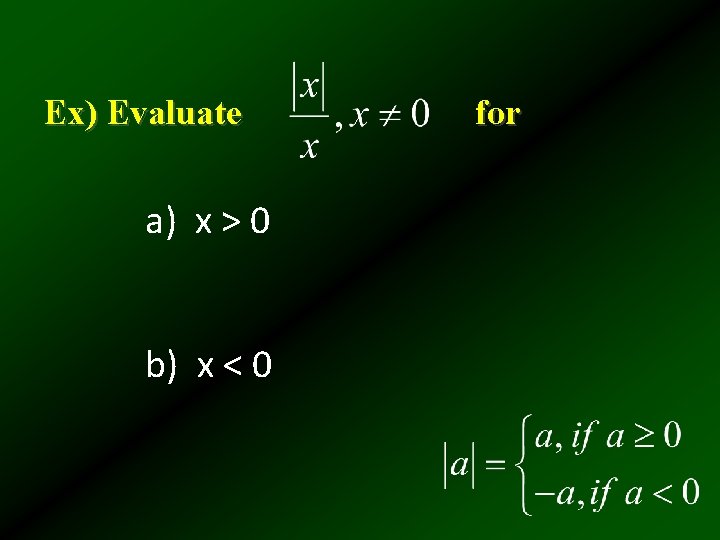
Ex) Evaluate a) x > 0 b) x < 0 for

Ex) Evaluate

Distance Between Two Points on the Real Number Line: Let a and b be real numbers. The distance between a and b is Ex) Find the distance between a and b if a = x – 3 and b = 2 x – 3

Sneedlegrit: Find the d(a, b) if a = -x + 4 and b = 3 x HW: pg. 10 (6) pg. 10 (22, 26) write in interval notation also pg. 10 (33, 34, 36, 41, 42) pg. 11 (50, 52, 59, 62, 66) pg. 12 (76)