Warmup Identify the exponent the base number 1

Warm-up • Identify the exponent & the base number. 1) 24 2) -3 x 4 3) -3● 4 x 4) (4 x)2 5) Which of the above represents an exponential expression?

3. 1 Exponential Functions After completing today’s lesson, you will be able to: • Identify an exponential function • Determine the domain & range of an exponential function • Evaluate an exponential function • Describe phenomena as representing exponential growth or decay.

Something to think about • Which would you prefer? – A million dollars today – Or a penny which doubles every day for the next 30 days • This is one of the reasons we study exponents, their properties, and their inverses

Exponential Functions An exponential function is a function in terms of x, where x is an exponent in the function. It’s written in the form: Where a is nonzero and b is positive and b≠ 1. The constant a is known as the initial value, and b is known as the base.

Examples of exponential functions and non-examples Exponential Functions Non-ex. s of Exp. Func. How are these functions alike? What makes an exponential function?

Which are exponential functions? Why? a) c) b) d)

Computing values for x in exponential functions e) Compute the exact value for f(x) without a calculator, where x=0. Now you try it for x=2.

Use calculator to find the exp. Function from the table. x -2 -1 0 1 2 f(x) 6 3 3/2 ¾ 3/8

Natural Base e Put the function in your calculator and please observe the nature of the graph and its end behavior:

Natural base e Since the end behavior approaches a constant, we can state:

Exponential Functions Any exp. Function written as: can be Where k is an appropriately chosen real number.

Exploration Turn to page 280. Do Exploration 1, answer all the question in the activity. After you are done, please answer this question: By looking at the graphs, what would each set of functions be: exponential growth, or decay?

Exponential Growth/Decay Functions Exponential Growth, if and ex. Exponential Decay, if ex. and

Review of Transformations: with Exponential functions Where a is responsible for vertical stretch/shrink, and k is horizontal stretch/shrink. Phase shifts occur horizontally from the constant h, and vertically from j.

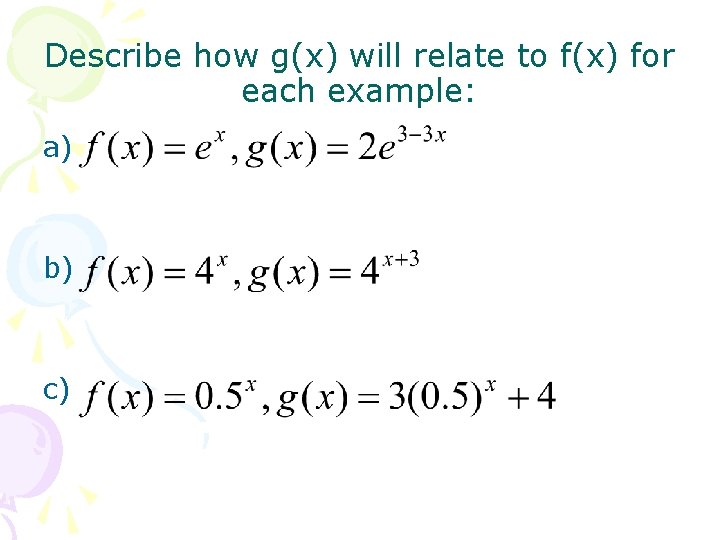
Describe how g(x) will relate to f(x) for each example: a) b) c)