WarmUp Exercises Solve each equation 3 Solve P

Warm-Up Exercises Solve each equation. 3. Solve P = 2 l + 2 w for w. ANSWER 4. P– 2 l W= 2 S is the complement of R. If m R = 38º, find m If T is also the complement of R, what is true about m S and m T? ANSWER 52º; m S=m T S.

Warm-Up 1 Exercises EXAMPLE Write reasons for each step Solve 2 x + 5 = 20 – 3 x. Write a reason for each step. Equation Explanation Reason Given 2 x + 5 = 20 – 3 x Write original equation. 2 x + 5 + 3 x =20 – 3 x + 3 x 5 x + 5 = 20 5 x = 15 x=3 Add 3 x to each side. Addition Property of Equality Combine like terms. Simplify. Subtract 5 from each side. Subtraction Property of Equality Divide each side by 5. Division Property of Equality

Warm-Up 2 Exercises EXAMPLE Use the Distributive Property Solve -4(11 x + 2) = 80. Write a reason for each step. SOLUTION Equation – 4(11 x + 2) = 80 – 44 x – 8 = 80 – 44 x = 88 x = – 2 Explanation Write original equation. Reason Multiply. Distributive Property Add 8 to each side. Addition Property of Equality Given Divide each side Division Property of Equality by – 44.

Warm-Up 3 Exercises EXAMPLE Use properties in the real world Heart Rate When you exercise, your target heart rate should be between 50% to 70% of your maximum heart rate. Your target heart rate r at 70% can be determined by the formula r = 0. 70(220 – a) where a represents your age in years. Solve the formula for a. SOLUTION Equation r = 0. 70(220 – a) r = 154 – 0. 70 a Explanation Write original equation. Multiply. Reason Given Distributive Property

Warm-Up 3 Exercises EXAMPLE Use properties in the real world Equation r – 154 = – 0. 70 a Explanation Reason Subtract 154 from Subtraction Property of Equality each side. r – 154 = a – 0. 70 Divide each side by – 0. 70. Division Property of Equality

Warm-Up Exercises GUIDED PRACTICE for Examples 1, 2 and 3 In Exercises 1 and 2, solve the equation and write a reason for each step. 1. 4 x + 9 = – 3 x + 2 Equation 4 x + 9 = – 3 x + 2 7 x + 9 = 2 7 x = – 7 x = – 1 Explanation Write original equation. Reason Add 3 x to each side. Addition Property of Equality Subtract 9 from each side. Divide each side by 7. Subtraction Property of Equality Given Division Property of Equality

Warm-Up Exercises GUIDED PRACTICE 2. for Examples 1, 2 and 3 14 x + 3(7 – x) = – 1 Equation 14 x + 3(7 – x) = – 1 Explanation Write original equation. Reason 14 x +21 - 3 x = – 1 Multiply. Distributive Property 11 x +21= – 1 Simplify Link the same value 11 x = – 22 Given Subtract 21 from Subtraction Property of each side. Equality x = – 2 Divide each side Division Property of Equality by 11.

Warm-Up Exercises GUIDED PRACTICE 3. for Examples 1, 2 and 3 Solve the formula A = 1 bh for b. 2 Formula Explanation Reason 1 bh 2 Write original equation. Given 2 A = bh Multiply Multiplication property 2 A = b h Divide Division property A=

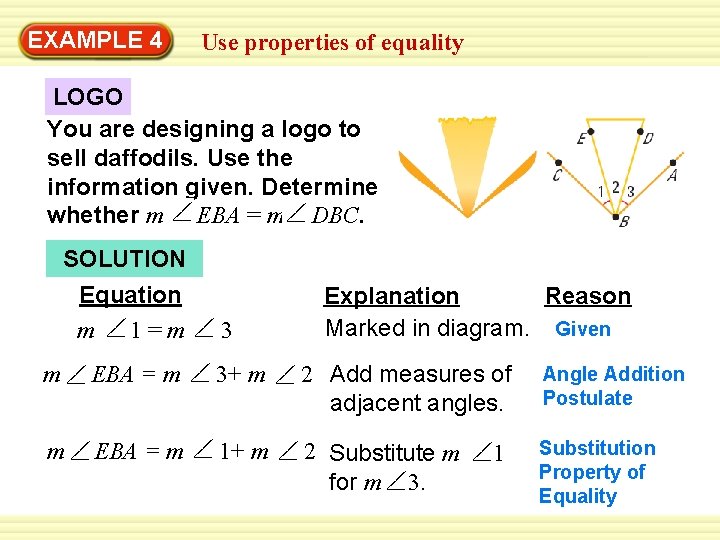
Warm-Up 4 Exercises EXAMPLE Use properties of equality LOGO You are designing a logo to sell daffodils. Use the information given. Determine whether m EBA = m DBC. SOLUTION Equation m 1=m 3 Explanation Reason Marked in diagram. Given m EBA = m 3+ m 2 Add measures of adjacent angles. Angle Addition Postulate m EBA = m 1+ m 2 Substitute m for m 3. Substitution Property of Equality 1

Warm-Up 4 Exercises EXAMPLE Use properties of equality m 1+m m 2 =m DBC Add measures of adjacent angles. EBA = m DBC Transitive Property Both measures of Equality are equal to the sum of m 1 +m 2. Angle Addition Postulate

Warm-Up 5 Exercises EXAMPLE Use properties of equality In the diagram, AB = CD. Show that AC = BD. SOLUTION Equation AB = CD Explanation Marked in diagram. Reason AC = AB + BC Add lengths of adjacent segments. Segment Addition Postulate BD = BC + CD Add lengths of adjacent segments. Segment Addition Postulate Given

Warm-Up 5 Exercises EXAMPLE Use properties of equality AB + BC = CD + BC Add BC to each side of AB = CD. Addition Property of Equality AC = BD Substitute AC for AB + BC and BD for BC + CD. Substitution Property of Equality

Warm-Up Exercises GUIDED PRACTICE for Examples 4 and 5 Name the property of equality the statement illustrates. 4. If m 6=m 7, then m 7=m 6. ANSWER Symmetric Property of Equality 5. If JK = KL and KL = 12, then JK = 12. ANSWER Transitive Property of Equality

Warm-Up Exercises GUIDED PRACTICE 6. m W=m for Examples 4 and 5 W ANSWER Reflexive Property of Equality

Daily Homework Quiz Warm-Up Exercises Solve. Give a reason for each step. 1. – 5 x + 18 = 3 x – 38 ANSWER Equation (Reason) – 5 x + 18 = 3 x – 38 (Given) – 8 x + 18 = – 38 (Subtr. Prop. Of Eq. ) – 8 x = – 56 (Subtr. Prop. Of Eq. ) x = 7 (Division Prop. Of Eq. )

Daily Homework Quiz Warm-Up Exercises Solve. Give a reason for each step. 2. – 3(x – 5) = 2(x + 10) ANSWER Equation (Reason) – 3(x – 5) = 2(x + 10) (Given) – 3 x + 15 = 2 x + 20 (Distributive Prop. ) 15 = 5 x +20 (Addition Prop. Of Eq. ) – 5 = 5 x (Subtr. Prop. Of Eq. ) – 1 = x (Division Prop. Of Eq. )

Daily Homework Quiz Warm-Up Exercises 3. If m 3=m 5 and m 5=m ANSWER Transitive Prop. Of Eq. 4. If CD = EF, then EF = CD. ANSWER Symmetric Prop. Of Eq. 8, then m 3=m 8.