WarmUp Exercises 2 5 4 Evaluate cos 60

  • Slides: 29
Download presentation
Warm-Up Exercises 2. 5, 4, Evaluate cos 60°. ( – lengths 5, 0. of

Warm-Up Exercises 2. 5, 4, Evaluate cos 60°. ( – lengths 5, 0. of the 0 and , ( – 5, 4 , Find the ( ANSWER ( 0, ( A triangle has vertices three sides of the triangle. ( 1. 41 ANSWER 0. 5 ANSWER 75 ANSWER 120 Evaluate the expression. 360 – 285 4. 840 – 2( 360 ( 3.

Lesson 12. 2

Lesson 12. 2

Your Notes

Your Notes

Example 1 Draw Angles in Standard Position Draw an angle with the given measure

Example 1 Draw Angles in Standard Position Draw an angle with the given measure in standard position. a. 215° b. 410° SOLUTION a. Because 215° is 35° more than 180°, the terminal side is 35° counterclockwise past the negative x-axis. c. – 60°

Example 1 Draw Angles in Standard Position b. Because 410° is 50° more than

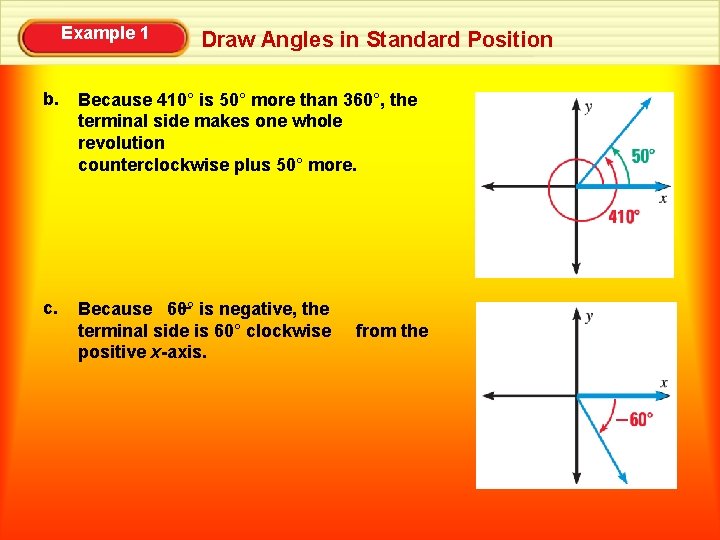
Example 1 Draw Angles in Standard Position b. Because 410° is 50° more than 360°, the terminal side makes one whole revolution counterclockwise plus 50° more. c. – is negative, the Because 60° terminal side is 60° clockwise positive x-axis. from the

Checkpoint Draw Angles in Standard Position Draw an angle with the given measure in

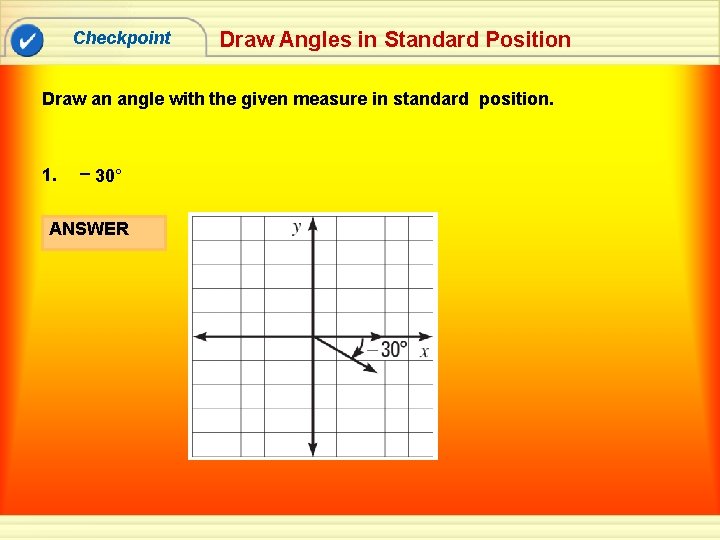
Checkpoint Draw Angles in Standard Position Draw an angle with the given measure in standard position. 1. – 30° ANSWER

Checkpoint Draw Angles in Standard Position Draw an angle with the given measure in

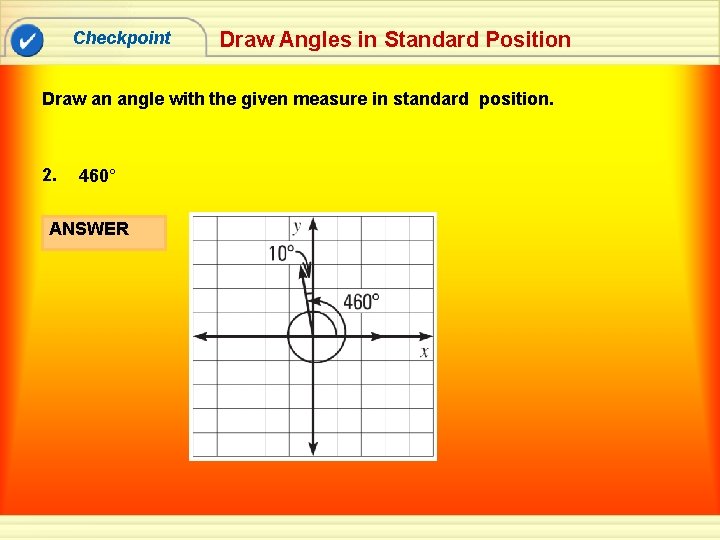
Checkpoint Draw Angles in Standard Position Draw an angle with the given measure in standard position. 2. 460° ANSWER

Checkpoint Draw Angles in Standard Position Draw an angle with the given measure in

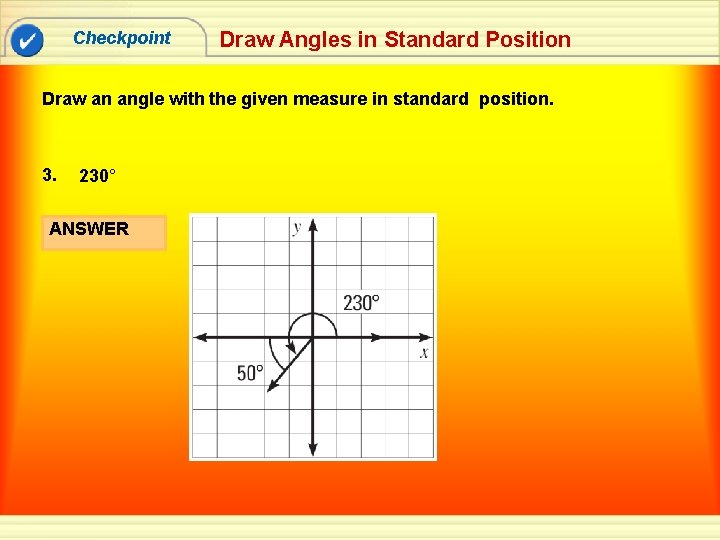
Checkpoint Draw Angles in Standard Position Draw an angle with the given measure in standard position. 3. 230° ANSWER

Checkpoint 4. Draw Angles in Standard Position Draw an angle with measure 90° in

Checkpoint 4. Draw Angles in Standard Position Draw an angle with measure 90° in standard position. On a different coordinate grid, draw an angle with measure 90° not in standard position. ANSWER

Example 2 Find Coterminal Angles Find one positive angle and one negative angle that

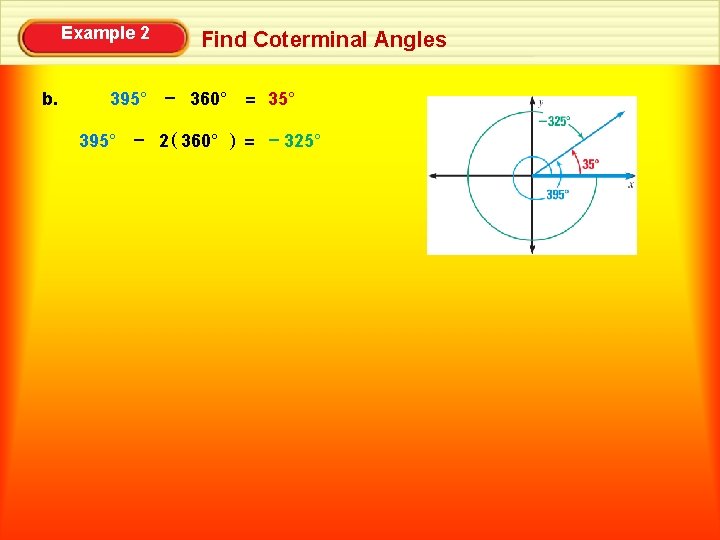
Example 2 Find Coterminal Angles Find one positive angle and one negative angle that are coterminal with the given angle. a. – 45° b. 395° SOLUTION There are many correct answers. Choose a multiple of 360° to add or subtract. a. – 45° + 360° = 315° – 45° – 360° = – 405°

Example 2 395° – 360° = 35° 395° – 2 ( 360° ( b.

Example 2 395° – 360° = 35° 395° – 2 ( 360° ( b. Find Coterminal Angles = – 325°

Checkpoint Find Coterminal Angles Find one positive angle and one negative angle that are

Checkpoint Find Coterminal Angles Find one positive angle and one negative angle that are coterminal with the given angle. – 310° 5. 50° ANSWER 410°, 6. 375° ANSWER 15°, – 345° 7. – 70° ANSWER 290°, – 430°

Example 3 Evaluate Trigonometric Functions Given a Point Let (4, -3) be a point

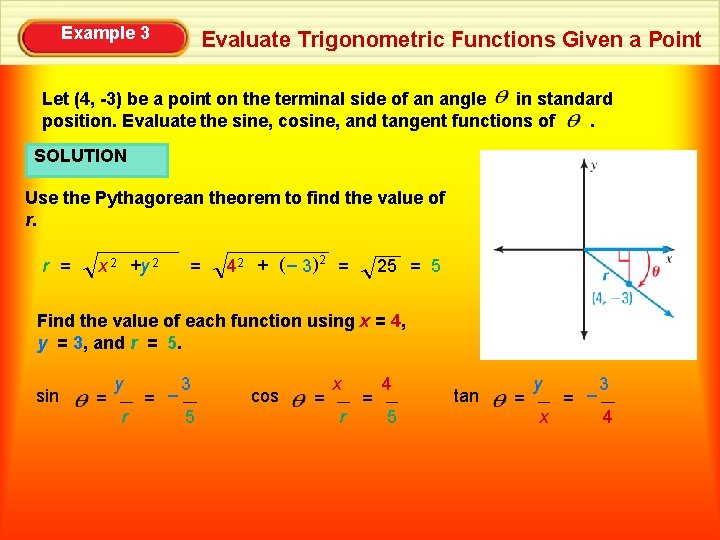
Example 3 Evaluate Trigonometric Functions Given a Point Let (4, -3) be a point on the terminal side of an angle in standard position. Evaluate the sine, cosine, and tangent functions of. SOLUTION Use the Pythagorean theorem to find the value of r. r = x 2 +y 2 = 4 2 + ( – 3 )2 = 25 = 5 Find the value of each function using x = 4, y = 3, and r = 5. sin = y r = – 3 5 cos = x r = 4 5 tan = y x = – 3 4

Checkpoint Evaluate Trigonometric Functions Given a Point Use the given point on the terminal

Checkpoint Evaluate Trigonometric Functions Given a Point Use the given point on the terminal side of an angle in standard position. Evaluate the sine, cosine, and tangent functions of. 8. ( – 3, 4 ) ANSWER sin = 4 5 , cos = – 3 5 , tan = – 4 3

Checkpoint Evaluate Trigonometric Functions Given a Point Use the given point on the terminal

Checkpoint Evaluate Trigonometric Functions Given a Point Use the given point on the terminal side of an angle in standard position. Evaluate the sine, cosine, and tangent functions of. 9. ( 6, 8 ) ANSWER sin = 4 5 , cos = 3 5 , tan = 4 3

Checkpoint Evaluate Trigonometric Functions Given a Point Use the given point on the terminal

Checkpoint Evaluate Trigonometric Functions Given a Point Use the given point on the terminal side of an angle in standard position. Evaluate the sine, cosine, and tangent functions of. 10. ( – 8, 15 ) ANSWER sin = 15 17 , cos = – 8 17 , tan = – 15 8

Example 4 Trigonometric Functions of a Quadrantal Angle Evaluate the sine, cosine, and tangent

Example 4 Trigonometric Functions of a Quadrantal Angle Evaluate the sine, cosine, and tangent functions of q = 180°. SOLUTION When q sin cos tan = 180°, you know that x = - r and y q = q = y r x r y x = = = 0 r –r r 0 –r = 0 = – 1 = 0.

Example 5 Positive and Negative Trigonometric Functions Determine whether the sine, cosine, and tangent

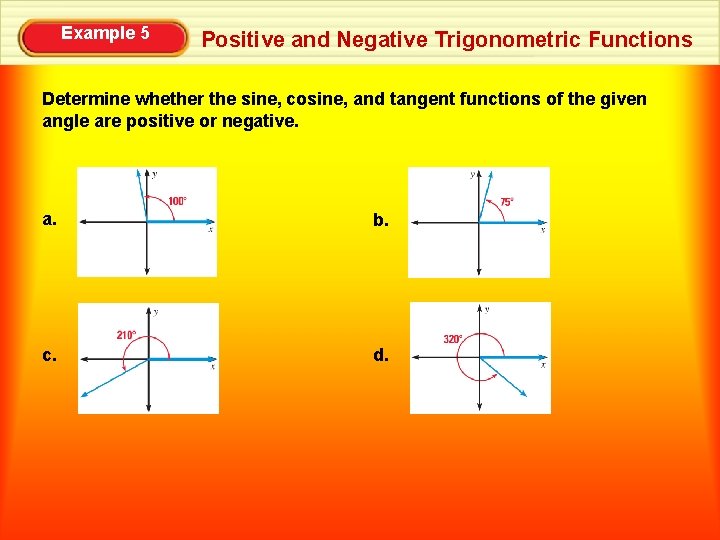
Example 5 Positive and Negative Trigonometric Functions Determine whether the sine, cosine, and tangent functions of the given angle are positive or negative. a. b. c. d.

Example 5 Positive and Negative Trigonometric Functions SOLUTION a. Because the terminal side lies

Example 5 Positive and Negative Trigonometric Functions SOLUTION a. Because the terminal side lies in Quadrant II, sin 100° is positive, cos 100° is negative, and tan 100° is negative. b. Because the terminal side lies in Quadrant I, sin 75° is positive, cos 75° is positive, and tan 75° is positive. c. Because the terminal side lies in Quadrant III, sin 210° Is negative, cos 210° is negative, and tan 210° is positive. d. Because the terminal side lies in Quadrant IV, sin 320° is negative, cos 320° is positive, and tan 320° is negative.

Checkpoint 11. Positive and Negative Trigonometric Functions Evaluate the sine, cosine, and tangent functions

Checkpoint 11. Positive and Negative Trigonometric Functions Evaluate the sine, cosine, and tangent functions of ANSWER sin 90° =1, cos 90° q = 90°. 0, =tan 90° is undefined Determine whether the sine, cosine, and tangent functions of the angle are positive or negative. 12. 40° ANSWER all positive

Checkpoint Positive and Negative Trigonometric Functions Determine whether the sine, cosine, and tangent functions

Checkpoint Positive and Negative Trigonometric Functions Determine whether the sine, cosine, and tangent functions of the angle are positive or negative. 13. 150° ANSWER The sine is positive, the cosine is negative, and the tangent is negative. 14. 225° ANSWER The sine is negative, the cosine is negative, and the tangent is positive.

VOLLEYBALL players spike the ball at speeds up to 100 miles per hour to

VOLLEYBALL players spike the ball at speeds up to 100 miles per hour to prevent the opponent from being able to return the ball.

Slip

Slip

WarmUp Exercises 1 Evaluate ANSWER 2 Evaluate ANSWERWarmUp Exercises 1 Evaluate ANSWER 2 Evaluate ANSWER
WarmUp Exercises WarmUp In Exercises 1 and 2WarmUp Exercises WarmUp In Exercises 1 and 2
WarmUp Exercises WarmUp In Exercises 1 and 2WarmUp Exercises WarmUp In Exercises 1 and 2
WarmUp Pg 462 59 WarmUp WarmUp Cos adjacentWarmUp Pg 462 59 WarmUp WarmUp Cos adjacent
Relations Exercises Exercises In the exercises below takeRelations Exercises Exercises In the exercises below take
Warmup Warmup Warmup Warmup Agenda n n nWarmup Warmup Warmup Warmup Agenda n n n
WarmUp Exercises Use this diagram for Exercises 1WarmUp Exercises Use this diagram for Exercises 1
WarmUp Exercises In Exercises 1 4 use A0WarmUp Exercises In Exercises 1 4 use A0
WarmUp Exercises Use this diagram for Exercises 1WarmUp Exercises Use this diagram for Exercises 1
WarmUp Exercises In Exercises 1 4 use A0WarmUp Exercises In Exercises 1 4 use A0
WarmUp Exercises Use this diagram for Exercises 1WarmUp Exercises Use this diagram for Exercises 1
WarmUp Exercises In Exercises 1 4 use A0WarmUp Exercises In Exercises 1 4 use A0
WarmUp Exercises Evaluate the expression when x 4WarmUp Exercises Evaluate the expression when x 4
WarmUp Exercises Evaluate the logarithm 1 log 5WarmUp Exercises Evaluate the logarithm 1 log 5
WarmUp Exercises 1 Evaluate 3 x 5 yWarmUp Exercises 1 Evaluate 3 x 5 y
WarmUp Exercises Evaluate each expression 1 10 22WarmUp Exercises Evaluate each expression 1 10 22
WarmUp Exercises 1 Evaluate 3 x 5 yWarmUp Exercises 1 Evaluate 3 x 5 y
WarmUp Exercises Evaluate the expression when x 4WarmUp Exercises Evaluate the expression when x 4
WarmUp Exercises Evaluate the expression 1 49 ANSWERWarmUp Exercises Evaluate the expression 1 49 ANSWER
WarmUp Exercises ab 1 Evaluate if a 5WarmUp Exercises ab 1 Evaluate if a 5
24 Warmup Evaluate Evaluate The Trapezoidal Rule Sec24 Warmup Evaluate Evaluate The Trapezoidal Rule Sec
WarmUp Exercises WARMUP PROBLEM Simplify the expression AssumeWarmUp Exercises WARMUP PROBLEM Simplify the expression Assume
Cronnelly Warmup Warmup Warmup Step 1 Order NumbersCronnelly Warmup Warmup Warmup Step 1 Order Numbers
Definition Active assistive exercises are exercises performed byDefinition Active assistive exercises are exercises performed by