WarmUp Determining End Behavior Match each function with

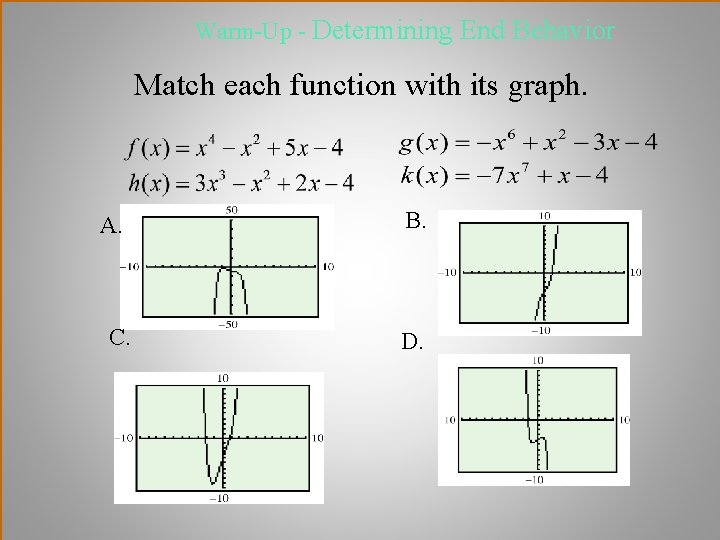
Warm-Up - Determining End Behavior Match each function with its graph. A. C. B. D.

Essential Question: How do you determine the shape and symmetry of the graph by the polynomial equation?

Even, Odd, or Neither Functions Not to be confused with End behavior To determine End Behavior, we check to see if the leading degree is even or odd With Functions, we are determining symmetry (if the entire function is even, odd, or neither)

Even and Odd Functions (algebraically) A function is even if f(-x) = f(x) If you plug in x and -x and get the same solution, then it’s even. Also: It is symmetrical over the y-axis. A function is odd if f(-x) = -f(x) If you plug in x and -x and get opposite solutions, then it’s odd.

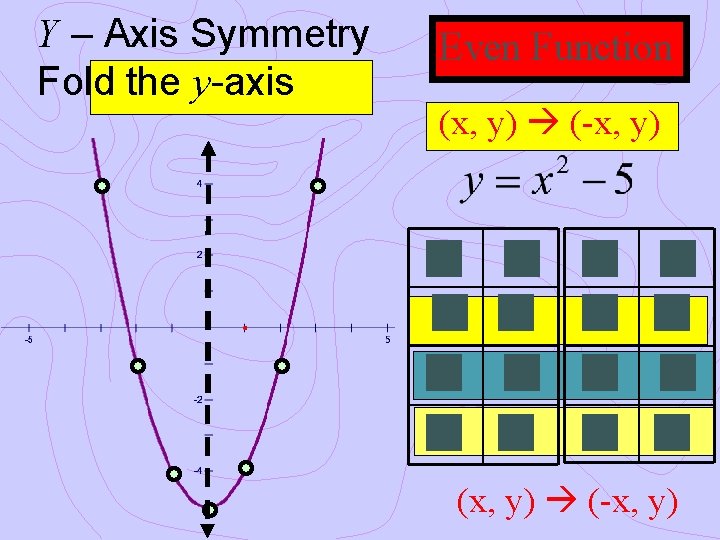
Y – Axis Symmetry Fold the y-axis Even Function (x, y) (-x, y) 0 -5 4 11 1 -4 -1 -4 2 -1 -2 -1 3 4 -3 4 (x, y) (-x, y)

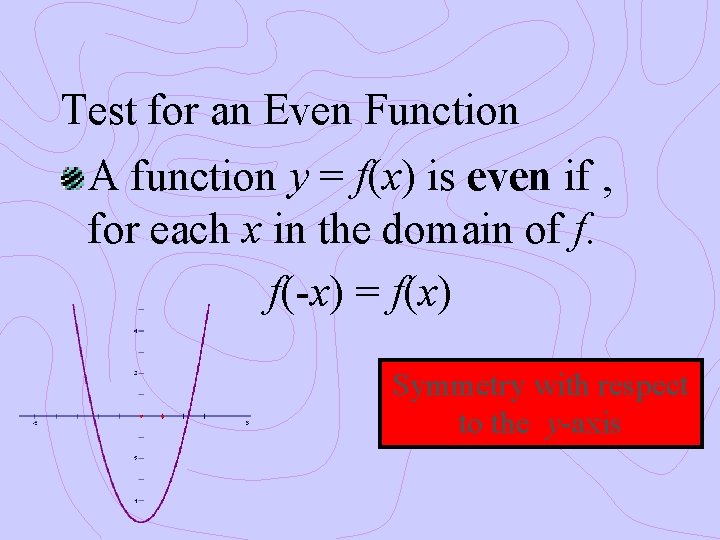
Test for an Even Function A function y = f(x) is even if , for each x in the domain of f. f(-x) = f(x) Symmetry with respect to the y-axis

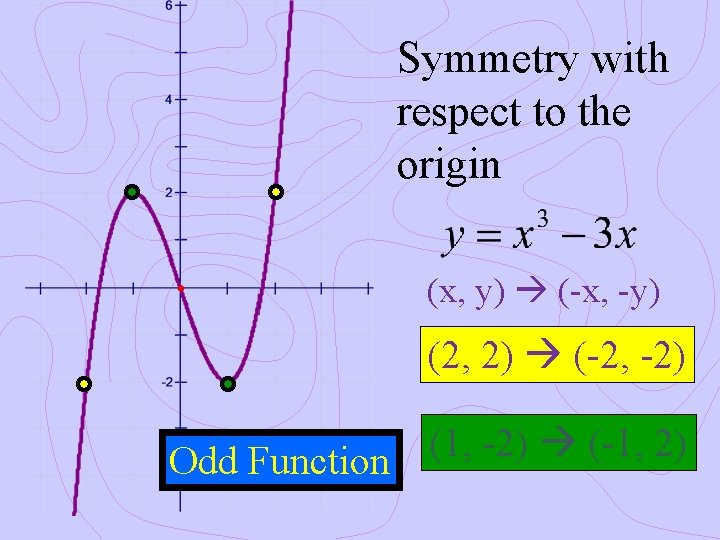
Symmetry with respect to the origin (x, y) (-x, -y) (2, 2) (-2, -2) (1, -2) (-1, 2) Odd Function

Test for an Odd Function A function y = f(x) is odd if , for each x in the domain of f. f(-x) = -f(x) Symmetry with respect to the Origin

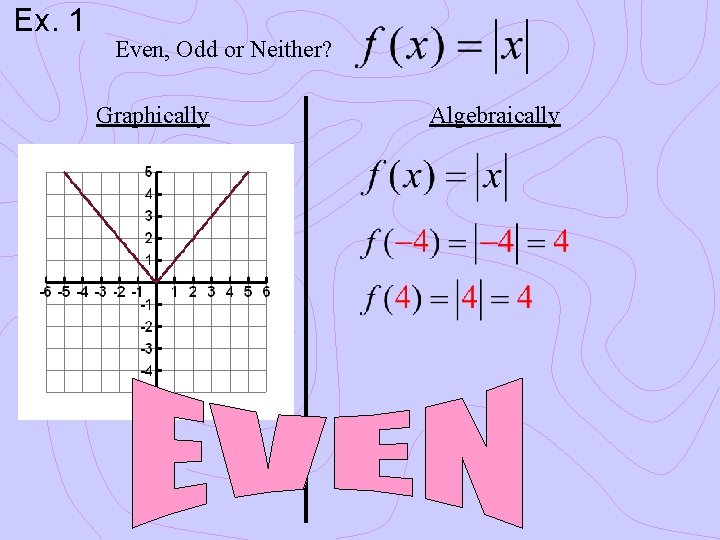
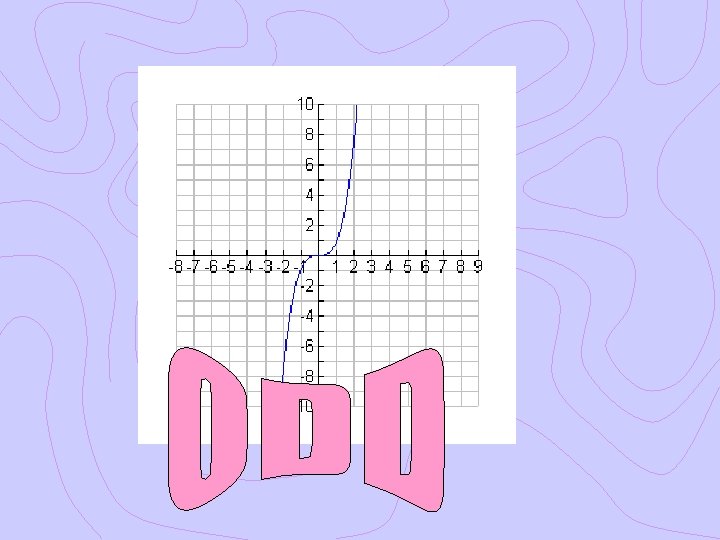
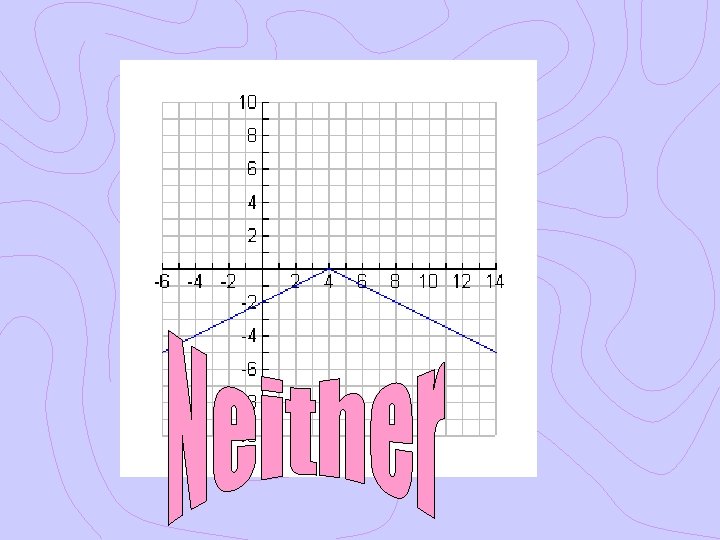
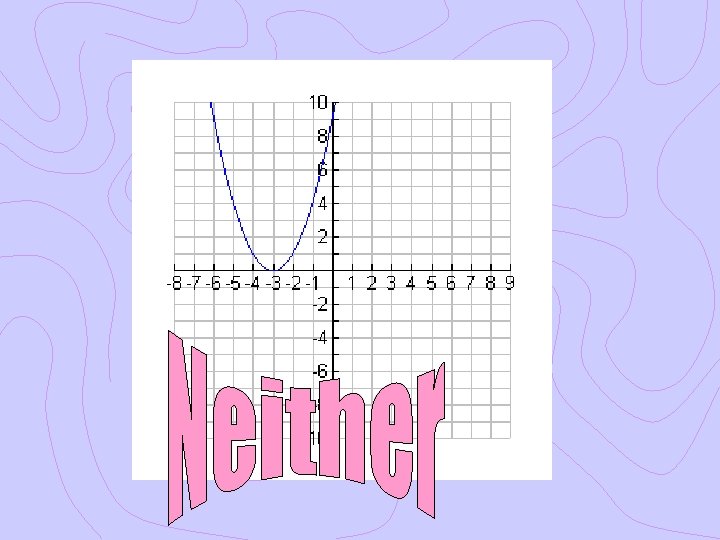
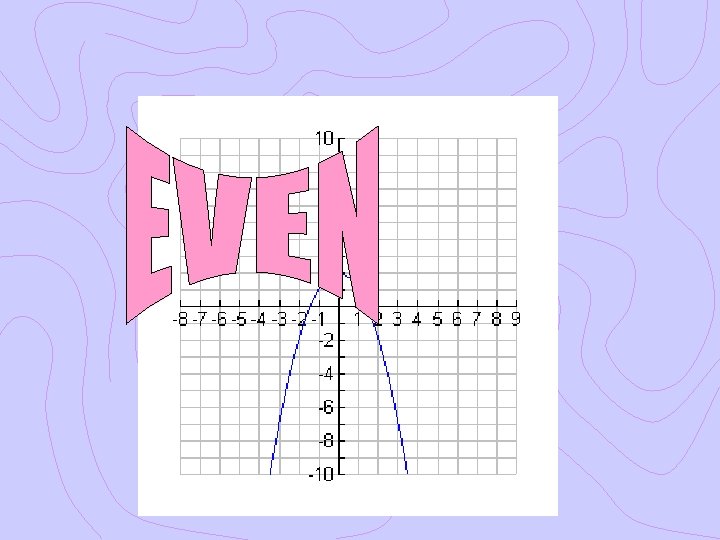
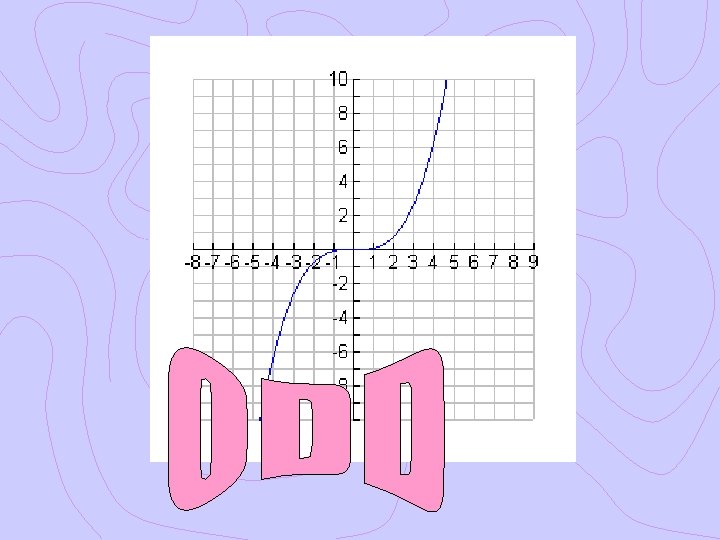
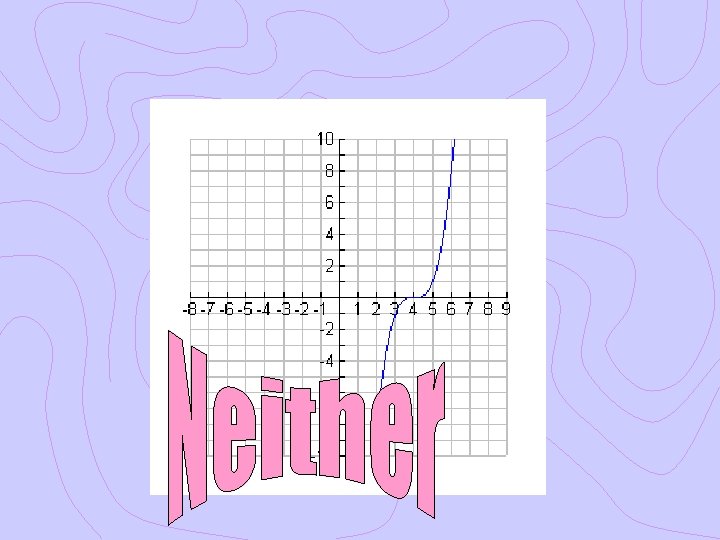
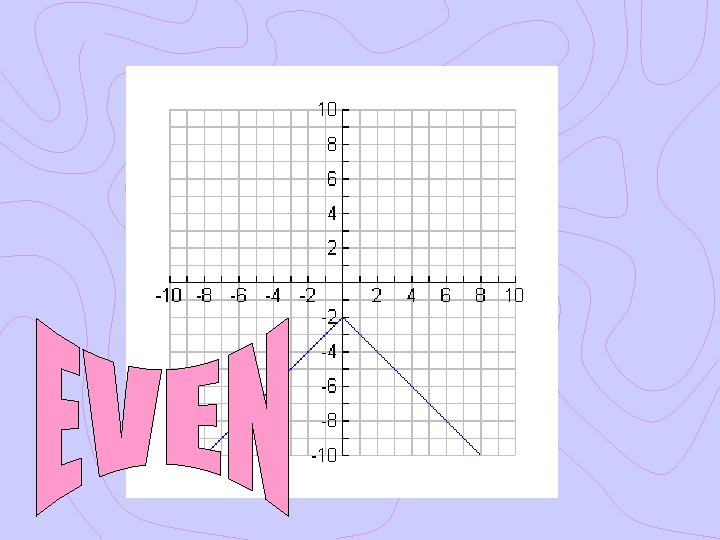
Ex. 1 Even, Odd or Neither? Graphically Algebraically

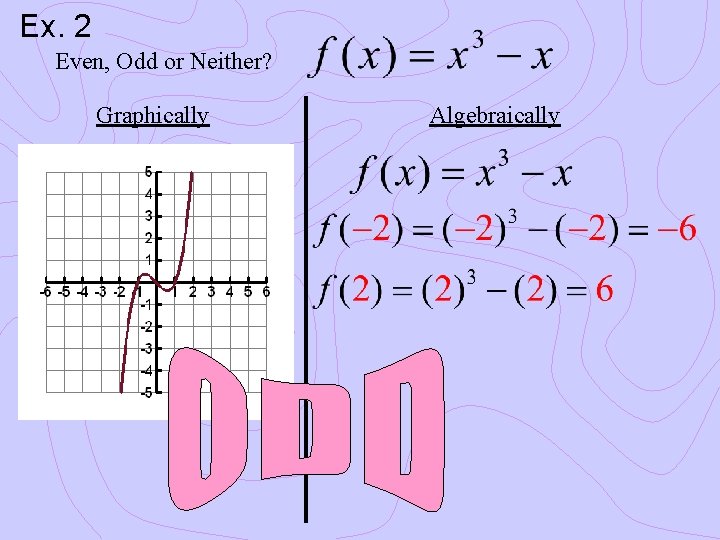
Ex. 2 Even, Odd or Neither? Graphically Algebraically

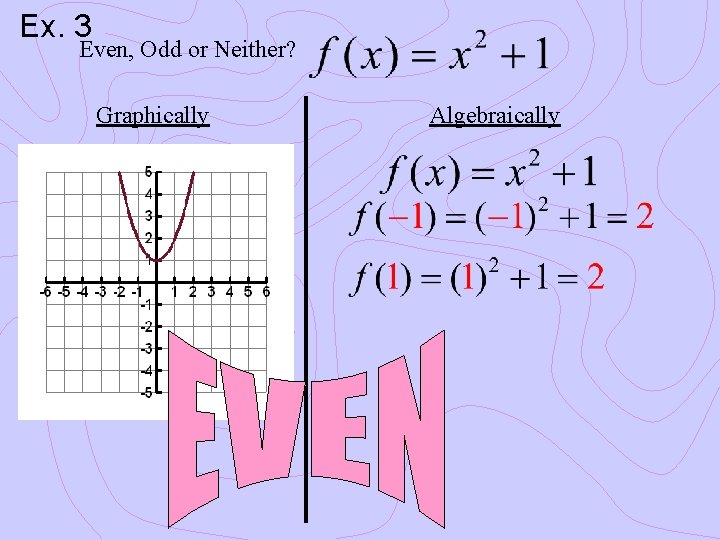
Ex. 3 Even, Odd or Neither? Graphically Algebraically

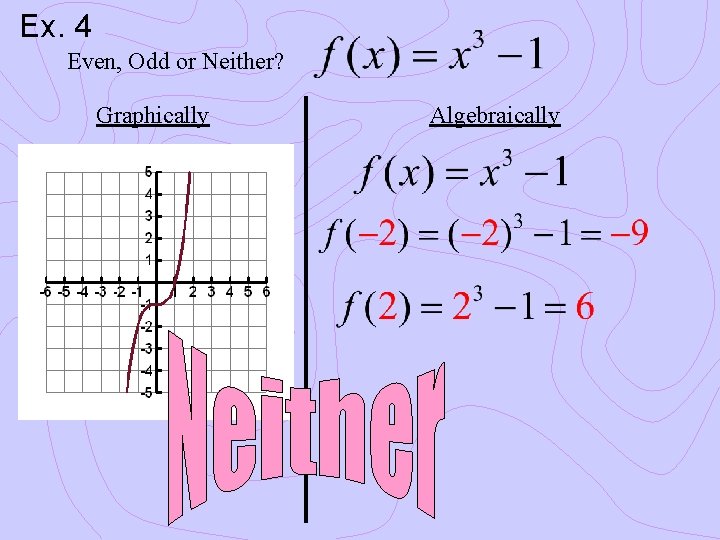
Ex. 4 Even, Odd or Neither? Graphically Algebraically

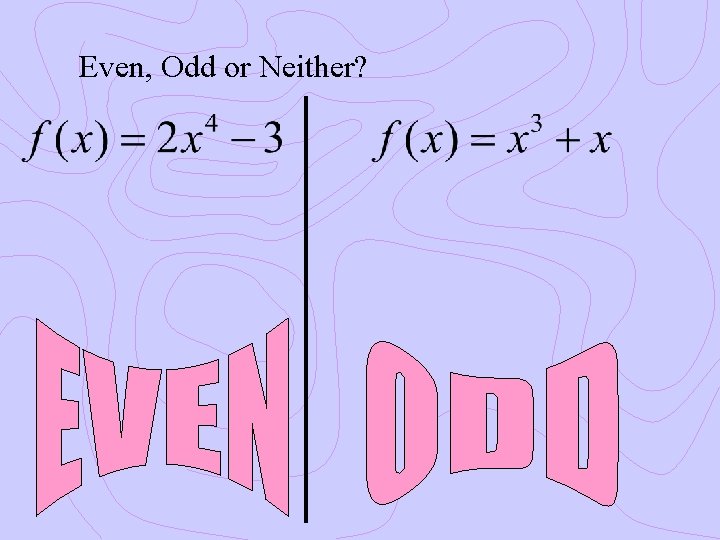
Even, Odd or Neither?

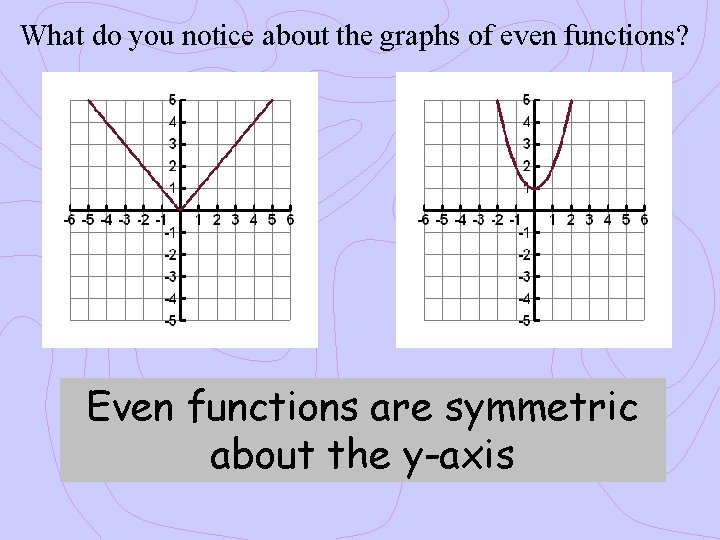
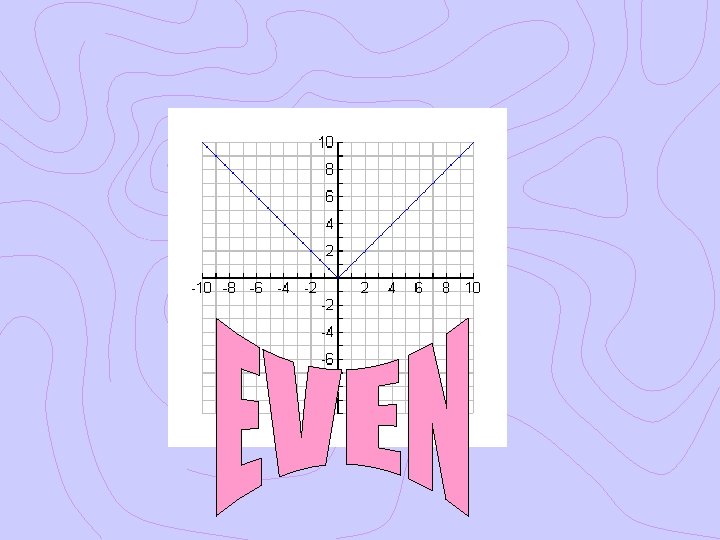
What do you notice about the graphs of even functions? Even functions are symmetric about the y-axis

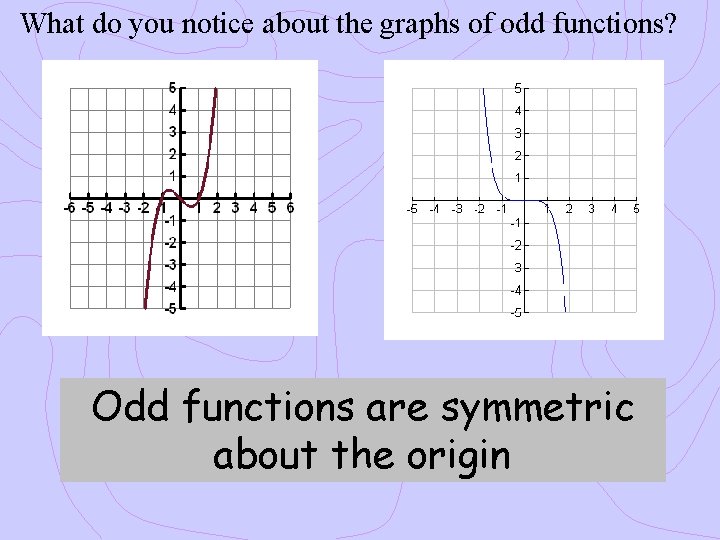
What do you notice about the graphs of odd functions? Odd functions are symmetric about the origin