WarmUp 4 1 Antiderivatives Indefinite Integrals Objectives Define

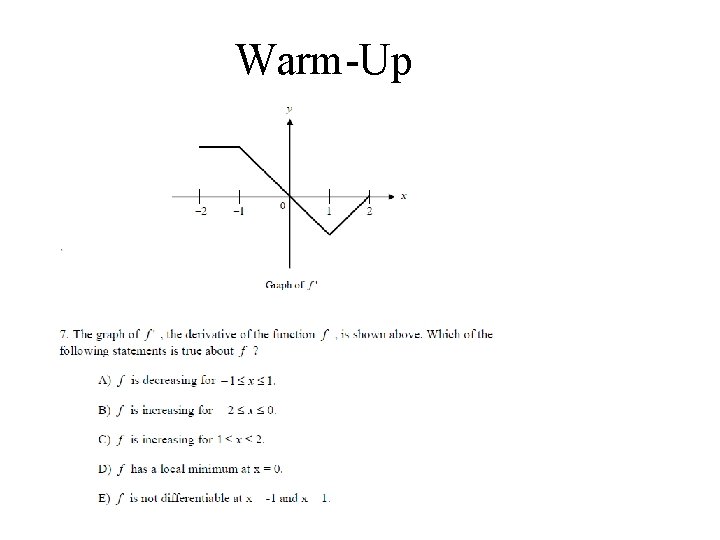
Warm-Up

4 -1: Antiderivatives & Indefinite Integrals Objectives: • Define the antiderivative (indefinite integral) • Learn basic antidifferentiation rules • Solve simple differential equations © 2002 Roy L. Gover (www. mrgover. com)

Definition If F(x) is an antiderivative of f(x) on an interval I, then F’ (x)=f(x) + c where c is a constant.

Example Let be an antiderivative of f(x) then

The Problem. . . Find the function given its derivative. The function is the antiderivative or indefinite integral.

Example If , find f(x), the function whose derivative is. Confirm your answer.

Try This If , find f(x), the function whose derivative is. Confirm your answer.

Try This If , find f(x), the function whose derivative is. aka the power rule for integration.

Example Find the antiderivative of 2 x 2.

Example Find the antiderivative of cos x.

Try This Find the antiderivative of sin x. -cos x+c

Example Find the general solution of the differential equation:

The general solution to: is: y=4 x+c because:

Important Idea Multiple solutions exist because:

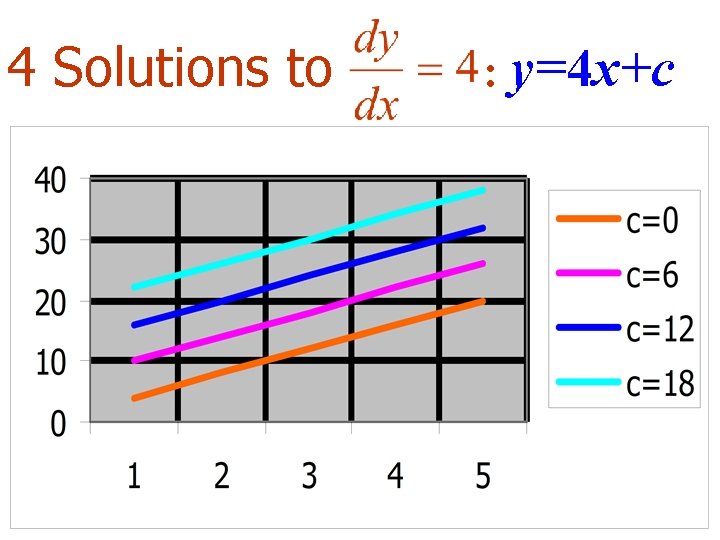
4 Solutions to : y=4 x+c

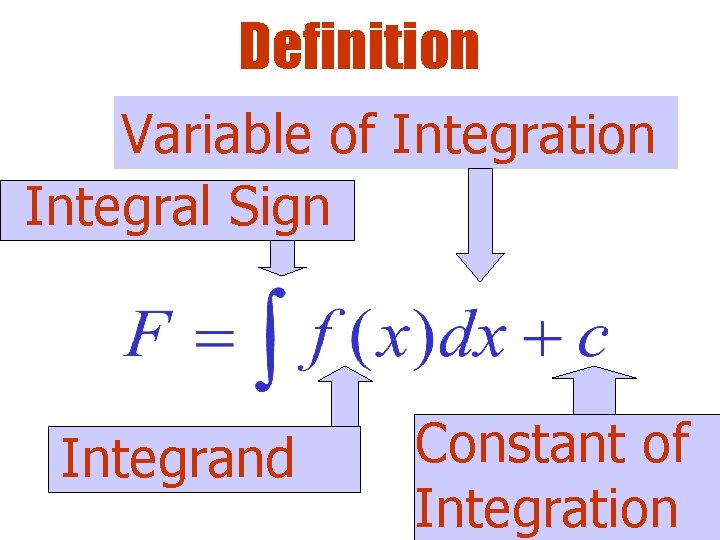
Definition Variable of Integration Integral Sign Integrand Constant of Integration

Example Find the antiderivative:

Definition Power Rule for Integration Special Case:

Definition Sum& Difference Rule for Integration The integral of the difference sum is is the difference of the sum of the integrals… integrals

Example Evaluate the indefinite integral:

Try This Find the antiderivative: Hint: re-write and use the power rule.

Assignment page 255 9 -14 all, 15 -27 odd

$Warm-Up Find the antiderivative: Hint: Re-write as 2 fractions.$

Warm-Up Find the antiderivative: Hint: Re-write as 2 fractions.

Solution

Example Evaluate the indefinite integral:

Lesson Close See page 250 of your text for basic integration rules. e z i Since integration is the r o m inverse of differentiation, you e M most of the already know rules.

Intro to Differential Equations. We need to do some work on Differential equations…

Example Sometimes we want a particular antiderivative. . . Find the equation for y given that y’=2 x+3 and y passes through the point (2, 1)

Example Find the equation for y given that y’=2 x+3 and y passes through the point (2, 1)

You try Find the general solution of F'(x) = x 3 + 2 x and the particular solution passing through point (2, 6) Note: (2, 6) means F(2) = 6

Particular Solutions Find the general solution of F'(x) = x 3 + 2 x and the particular solution passing through point (2, 6) F(x) = ∫x 3 + 2 x 4 2 =x +x +C general solution 4 -2 = c F(2) = 6 = 24 + 22 + C 4 F(x) = x 4 + x 2 - 2 particular solution 4

Solving a Problem A ball is thrown upward with an initial velocity of 64 feet per second from an initial height of 80 feet. a) Find the position function giving the height s as a function of time t. b) When does the ball hit the ground?

Assignment page 255 #35 -41 odd, 55 -61 odd, 63, 69.

QR code activity 1) If you do not have a QR code scanner, partner with someone who does. 2) Choose a random QR Code to scan, and solve the given problem. 3) In the appropriate blank, record your answer and justification on the back of your worksheet. 4) Use that answer to find the next problem. (e. g. The answer to #7 should be at the bottom of the QR code for #8)

Solving a Problem A ball is thrown upward with an initial velocity of 64 feet per second from an initial height of 80 feet. a) Find the position function giving the height s as a function of time t. b) When does the ball hit the ground? position = s velocity = s' acceleration = s'' s' = ∫s'' = ∫-32 feet/sec s' = -32 t + c How can we find c?

Solving a Problem A ball is thrown upward with an initial velocity of 64 feet per second from an initial height of 80 feet. a) Find the position function giving the height s as a function of time t. b) position When does=the ground? s ball hitvelocity = s' acceleration = s'' s' = -32 t + c initial velocity is 64 when time is zero 64 = -32(0) + c 64 = c s' = -32 t + 64

Solving a Problem A ball is thrown upward with an initial velocity of 64 feet per second from an initial height of 80 feet. a) Find the position function giving the height s as a function of time t. b) position When does=the ground? s ball hitvelocity = s' acceleration = s'' s = ∫s' = ∫-32 t + 64 2 s = -32 t + 64 t + c 2 How do we find c this time?

Solving a Problem A ball is thrown upward with an initial velocity of 64 feet per second from an initial height of 80 feet. a) Find the position function giving the height s as a function of time t. b) position When does=the ground? s ball hitvelocity = s' acceleration = s'' s = -32 t + 64 t + c 2 2 initial height is 80 (time is 0) 80 = -32(0) + 64(0) + c 2 80 = c 2

Solving a Problem A ball is thrown upward with an initial velocity of 64 feet per second from an initial height of 80 feet. a) Find the position function giving the height s as a function of time t. b) position When does=the ground? s ball hitvelocity = s' acceleration = s'' 2 80 = -32(0) 2 80 = c + 64(0) + c s = -16 t 2 +64 t + 80 So when does the ball hit the ground?

Solving a Problem A ball is thrown upward with an initial velocity of 64 feet per second from an initial height of 80 feet. a) Find the position function giving the height s as a function of time t. b) When does the ball hit the ground? s = -16 t 2 +64 t + 80 The position will be zero. 0 = -16 t 2 +64 t + 80 0 = -16(t - 5)(t + 1) t = 5 or -1