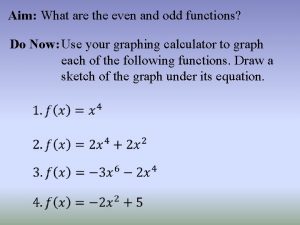WarmUp 1 Unit 6 324 even 327 odd

  • Slides: 18
Download presentation
Warm-Up #1 Unit 6 3/24 – even 3/27 - odd

Warm-Up #1 Unit 6 3/24 – even 3/27 - odd

DON’T FORGET YOUR WEEK 1 USA TEST PREP IS DUE TODAY!!! ü 10 ASSIGNMENTS

DON’T FORGET YOUR WEEK 1 USA TEST PREP IS DUE TODAY!!! ü 10 ASSIGNMENTS

GSE Algebra I UNIT QUESTION: How can I represent, compare, and interpret sets of

GSE Algebra I UNIT QUESTION: How can I represent, compare, and interpret sets of data? Standard: MCC 9 -12. S. ID. 1 -3, 5 -9, SP. 5 Today’s Question: How do I graphically represent data? Standard: MCC 9 -12. S. ID. 1

Unit 6 Day 1 Vocabulary Standards MCC 6. SP. 5 c, MCC 9 -12.

Unit 6 Day 1 Vocabulary Standards MCC 6. SP. 5 c, MCC 9 -12. S. ID. 1, MCC 9 -12. S. 1 D. 2 and MCC 9 -12. S. ID. 3

Box Plot A plot showing the minimum, maximum, first quartile, median, and third quartile

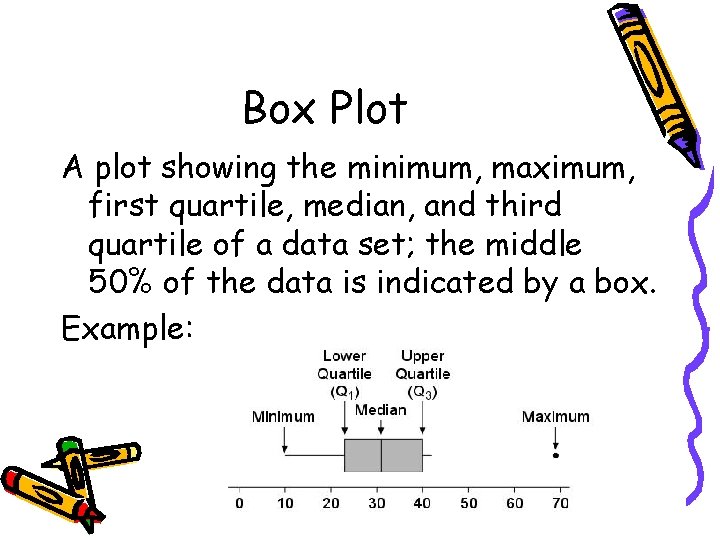
Box Plot A plot showing the minimum, maximum, first quartile, median, and third quartile of a data set; the middle 50% of the data is indicated by a box. Example:

Pros and Cons Advantages: • Shows 5 -point summary and outliers • Easily compares

Pros and Cons Advantages: • Shows 5 -point summary and outliers • Easily compares two or more data sets • Handles extremely large data sets easily Disadvantages: • Not as visually appealing as other graphs • Exact values not retained

Dot Plot A frequency plot that shows the number of times a response occurred

Dot Plot A frequency plot that shows the number of times a response occurred in a data set, where each data value is represented by a dot. Example:

Pros and Cons Advantages: • Simple to make • Shows each individual data point

Pros and Cons Advantages: • Simple to make • Shows each individual data point Disadvantages: • Can be time consuming with lots of data points to make • Have to count to get exact total. Fractions of units are hard to display.

Histogram A frequency plot that shows the number of times a response or range

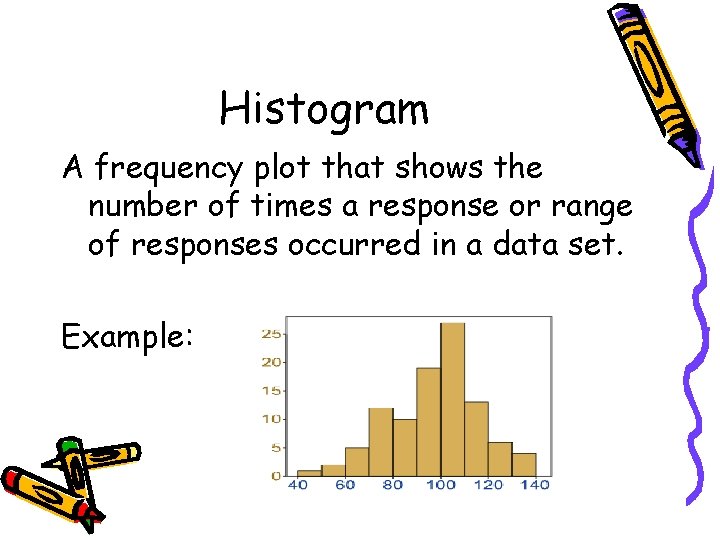
Histogram A frequency plot that shows the number of times a response or range of responses occurred in a data set. Example:

Pros and Cons Advantages: • Visually strong • Good for determining the shape of

Pros and Cons Advantages: • Visually strong • Good for determining the shape of the data Disadvantages: • Cannot read exact values because data is grouped into categories • More difficult to compare two data sets

Mean The average value of a data set, found by summing all values and

Mean The average value of a data set, found by summing all values and dividing by the number of data points Example: 5 + 4 + 2 + 6 + 3 = 20 The Mean is 4

Median The middle-most value of a data set; 50% of the data is less

Median The middle-most value of a data set; 50% of the data is less than this value, and 50% is greater than it Example:

First Quartile The value that identifies the lower 25% of the data; the median

First Quartile The value that identifies the lower 25% of the data; the median of the lower half of the data set; written as Example:

Third Quartile Value that identifies the upper 25% of the data; the median of

Third Quartile Value that identifies the upper 25% of the data; the median of the upper half of the data set; 75% of all data is less than this value; written as Example:

Interquartile Range The difference between the third and first quartiles; 50% of the data

Interquartile Range The difference between the third and first quartiles; 50% of the data is contained within this range Example: Subtract Third Quartile ( ) – First Quartile ( ) = IQR

Outlier A data value that is much greater than or much less than the

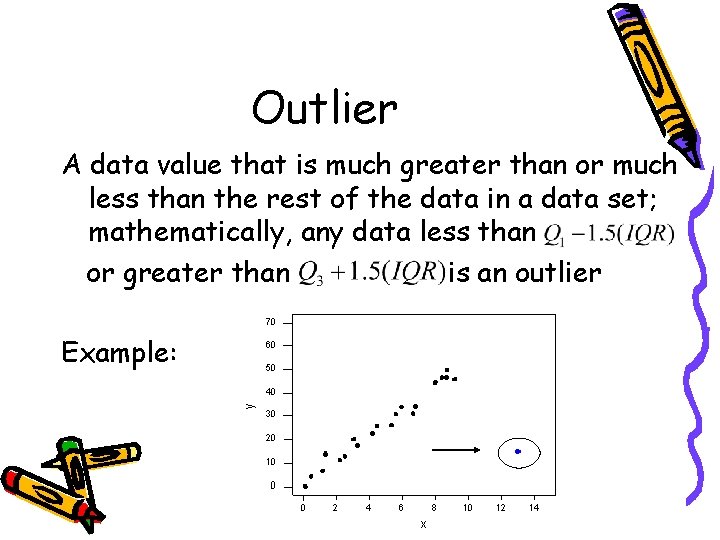
Outlier A data value that is much greater than or much less than the rest of the data in a data set; mathematically, any data less than or greater than is an outlier Example:

The numbers below represent the number of homeruns hit by players of the Hillgrove

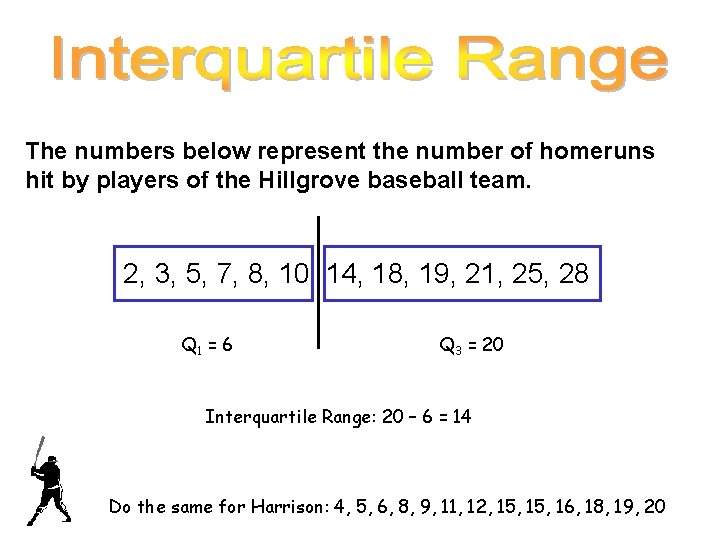
The numbers below represent the number of homeruns hit by players of the Hillgrove baseball team. 2, 3, 5, 7, 8, 10, 14, 18, 19, 21, 25, 28 Q 1 = 6 Q 3 = 20 Interquartile Range: 20 – 6 = 14 Do the same for Harrison: 4, 5, 6, 8, 9, 11, 12, 15, 16, 18, 19, 20

The numbers below represent the number of homeruns hit by players of the Hillgrove

The numbers below represent the number of homeruns hit by players of the Hillgrove baseball team. 2, 3, 5, 7, 8, 10, 14, 18, 19, 21, 25, 28 Q 1 = 6 Q 3 = 20 Interquartile Range: 20 – 6 = 14 6 12 20

Warm up 3 324 even 327 odd TheWarm up 3 324 even 327 odd The
0 0 1 Even 1 Odd Odd 10 0 1 Even 1 Odd Odd 1
Odd Todd and Even Steven This is OddOdd Todd and Even Steven This is Odd
Even s answer even questions Odd s answerEven s answer even questions Odd s answer
327 Solutions PLACEMENT CONSULTING 327 Solutions Inc 610327 Solutions PLACEMENT CONSULTING 327 Solutions Inc 610
BELLRINGER 324 and 327 1 SIT WITHNEAR WHOBELLRINGER 324 and 327 1 SIT WITHNEAR WHO
Warmup Warmup Warmup Warmup Agenda n n nWarmup Warmup Warmup Warmup Agenda n n n
20012004 2001 325 324 325 325 325 32420012004 2001 325 324 325 325 325 324
Transcription Page 319 324 Example problems Page 324Transcription Page 319 324 Example problems Page 324
Odd one out Which is the odd oneOdd one out Which is the odd one
Oppositional Defiant Disorder ODD What is ODD OppositionalOppositional Defiant Disorder ODD What is ODD Oppositional
Starter odd one out Which is the oddStarter odd one out Which is the odd
Nahosemenn rostliny odd CYKASY Cykas australsk odd JinanyNahosemenn rostliny odd CYKASY Cykas australsk odd Jinany
5 Network ODD Server ODD Control Server 15 Network ODD Server ODD Control Server 1
TAALPROBLEMEN ODD ONE OUT ODD ONE OUT PRINCIPETAALPROBLEMEN ODD ONE OUT ODD ONE OUT PRINCIPE
Odd Pie Fights Placing an odd number ofOdd Pie Fights Placing an odd number of
Induction and Recursion Odd Powers Are Odd FactInduction and Recursion Odd Powers Are Odd Fact