Warm up Write the following expressions in exponential

Warm up • Write the following expressions in exponential form • a) (2)(2) • b) (3 x)(3 x) • c) 2(xy)(xy)

We are Learning to…… Use the Exponent Laws

Exponent notation We use exponent notation to show repeated multiplication by the same number. For example: we can use exponent notation to write 2 × 2 × 2 as 25 Exponent or power base This number is read as ‘two to the power of five’. 25 = 2 × 2 × 2 = 32

Multiplying numbers in exponent form When we multiply two numbers written in exponent form and with the same base we can see an interesting result. For example: 34 × 32 = (3 × 3 × 3) × (3 × 3) =3× 3× 3× 3 = 36 = 3(4 + 2) 73 × 75 = (7 × 7) × (7 × 7 × 7) =7× 7× 7 = 78 = 7(3 + 5) When we multiply two numbers with the same base the What do you notice? exponents are added. In general, xm × xn = x(m + n) 4 of 70 © Boardworks Ltd 2005

Dividing numbers in exponent form When we divide two numbers written in exponent form and with the same base we can see another interesting result. For example: 45 ÷ 42 4× 4× 4 = 43 = 4(5 – 2) = 4× 4 56 ÷ 5 4 = 5× 5× 5× 5 = 52 = 5(6 – 4) 5× 5× 5× 5 When we divide two numbers with the same base the What do you notice? exponents are subtracted. In general, xm ÷ xn = x(m – n) 5 of 70 © Boardworks Ltd 2005

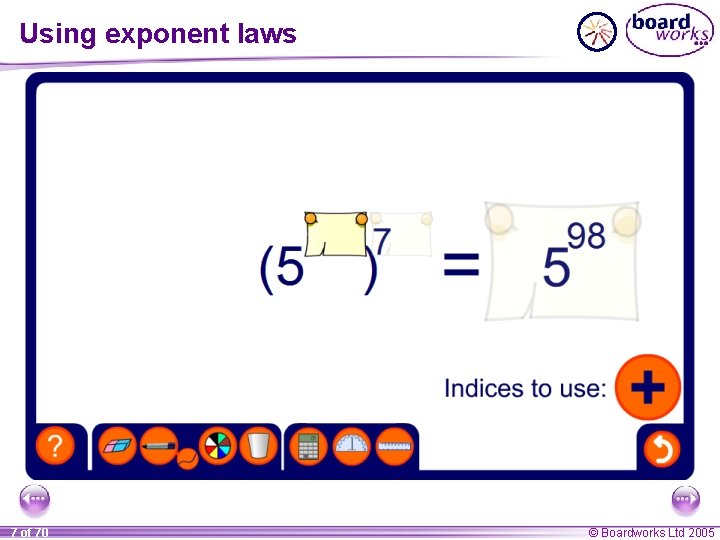
Raising a power to a power Sometimes numbers can be raised to a power and the result raised to another power. For example, (43)2 = 43 × 43 = (4 × 4) × (4 × 4) = 46 = 4(3 × 2) When a number is raised to a power and then raised to another What do you notice? power, the powers are multiplied. In general, (xm)n = xmn 6 of 70 © Boardworks Ltd 2005

Using exponent laws 7 of 70 © Boardworks Ltd 2005

The power of 1 Find the value of the following using your calculator: 61 471 0. 91 – 51 01 Any number raised to the power of 1 is equal to the number itself. In general, x 1 = x Because of this we don’t usually write the power when a number is raised to the power of 1. 8 of 70 © Boardworks Ltd 2005

The power of 0 Look at the following division: 64 ÷ 6 4 = 1 Using the second exponent law, 64 ÷ 64 = 6(4 – 4) = 60 That means that: 60 = 1 Any non-zero number raised to the power of 0 is equal to 1. For example, 100 = 1 9 of 70 3. 4520 = 1 723 538 5920 = 1 © Boardworks Ltd 2005

Exponent laws Here is a summary of the exponent laws you have met so far: xm × xn = x(m + n) xm ÷ xn = x(m – n) (xm)n = xmn x 1 = x x 0 = 1 (for x = 0) 10 of 70 © Boardworks Ltd 2005

Negative exponents Look at the following division: 3× 3× 3× 3 32 ÷ 3 4 = = 1 1 = 2 3 3× 3 Using the second exponent law, 32 ÷ 34 = 3(2 – 4) = 3– 2 That means that Similarly, 11 of 70 6– 1 = 1 6 3– 2 = 1 32 7– 4 = 1 74 and 5– 3 = 1 53 © Boardworks Ltd 2005

Reciprocals A number raised to the power of – 1 gives us the reciprocal of that number. The reciprocal of a number is what we multiply the number by to get 1. 1 The reciprocal of a is a The reciprocal of a b is b a We can find reciprocals on a calculator using the x-1 key. 12 of 70 © Boardworks Ltd 2005

Finding the reciprocals Find the reciprocals of the following: 1) 6 1 The reciprocal of 6 = 6 3 2) 7 3 7 The reciprocal of = 7 3 3) 0. 8 4 0. 8 = 5 4 5 The reciprocal of = 5 4 or 0. 8– 1 = 1. 25 13 of 70 or 6 -1 or 3 7 1 = 6 – 1 7 = 3 = 1. 25 © Boardworks Ltd 2005

Match the reciprocal pairs 14 of 70 © Boardworks Ltd 2005

• To succeed at this lesson today you need to know and be able to use… • 1. The five basic exponent laws • 2. Negative exponents • 3. Regular math laws for coefficients Nelson Page 222 #s 4 ace, 5 bdf, 6 bdf, 7 ace & 8 bdef