Warm Up Using the true conditional statement Constrictors

Warm Up Using the true conditional statement, “Constrictors such as pythons are not poisonous, ” write each of the following. 1. Rewrite the statement in if-then form. 2. Write the converse of the if-then statement. 3. Write the contrapositive of the if-then statement. 4. Write the hypothesis and conclusion of the if-then statement.

2. 2 Definitions and Biconditional Statements Advanced Geometry

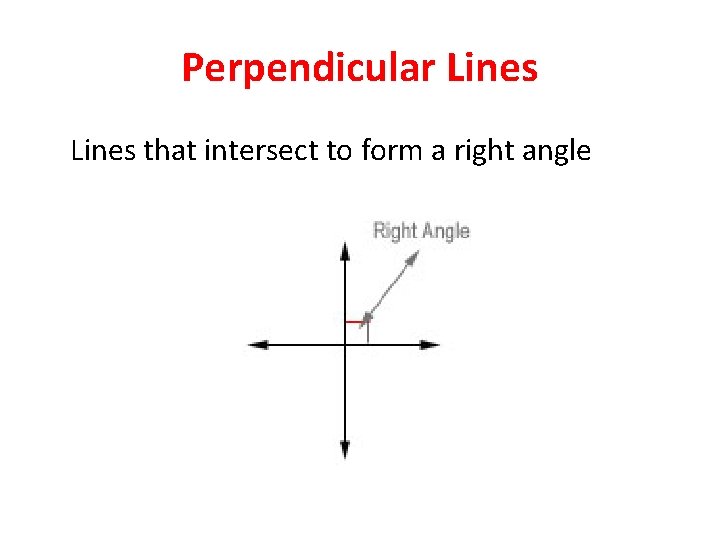
Perpendicular Lines that intersect to form a right angle

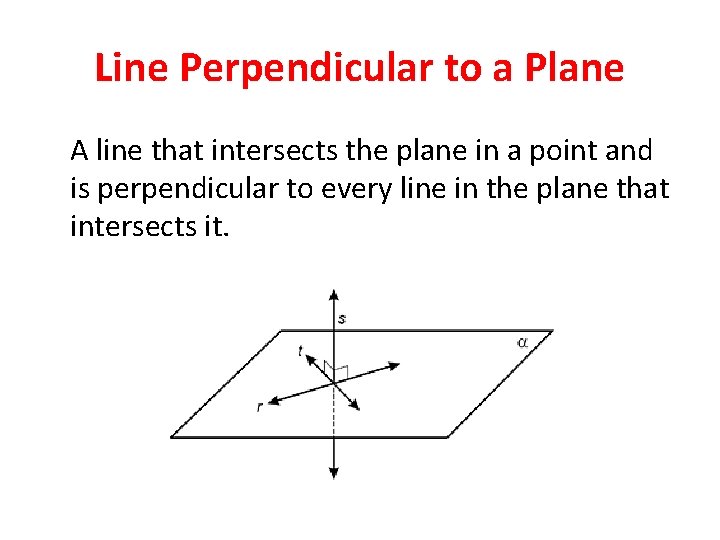
Line Perpendicular to a Plane A line that intersects the plane in a point and is perpendicular to every line in the plane that intersects it.

NOTE All definitions can be interpreted “forward” and “backward. ” (Conditional Statement and Converse)

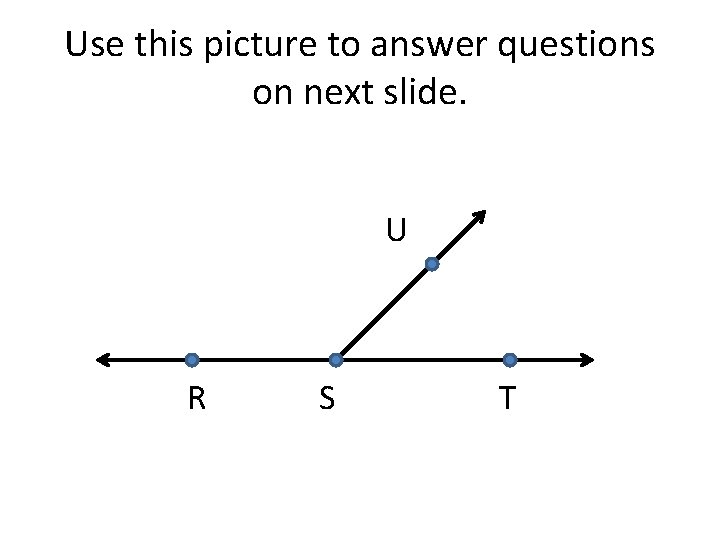
Use this picture to answer questions on next slide. U R S T

Using Definitions Decide whether each statement about the diagram is true. Explain your answer using the definitions you have learned. 1. Points R, S, and T are collinear 2. Ray SU is perpendicular to line RT

Biconditional Statements A statement that contains the phrase “if and only if. ” Conditional: If it is Saturday, then I am working at the restaurant. Biconditional: It is Saturday, if and only if I am working at the resaurant.

Examples Rewrite the biconditional statements as a conditional statement and its converse. 1. Three lines are coplanar if and only if they lie in the same plane. 2. Two lines intersect if and only if their intersection is exactly one point.

NOTE A biconditional statement can be either true or false. To be true, both the conditional statement and its converse must be true.

Examples For each statement. State whether the statement is biconditional or not, and find whether the statement is true or false. 1. X = 3 if and only if X squared = 9. 2. X squared is less than 49 if and only if X is less than 7. 3. X squared is 4 x if and only if X = 4.

Examples The following statements are true. Write the converse for each and decide whether they are true or false. If the converse if true, combine it with the original to form a biconditional. If the converse is false, state a counterexample. 1. If x squared is 4, then x is 2 or -2. 2. If two planes intersect, then they contain the same line. 3. If a number ends in 0, then the number is divisible by 5.