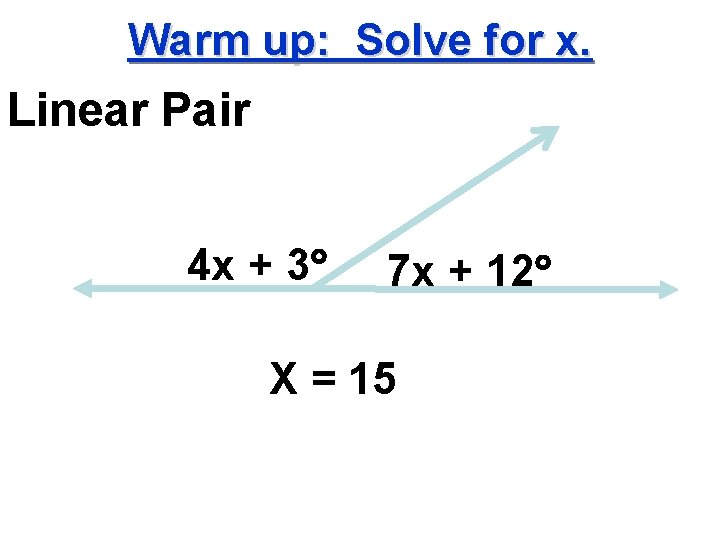
Warm up Solve for x Linear Pair 4

Warm up: Solve for x. Linear Pair 4 x + 3 7 x + 12 X = 15

Special Segments in Triangles

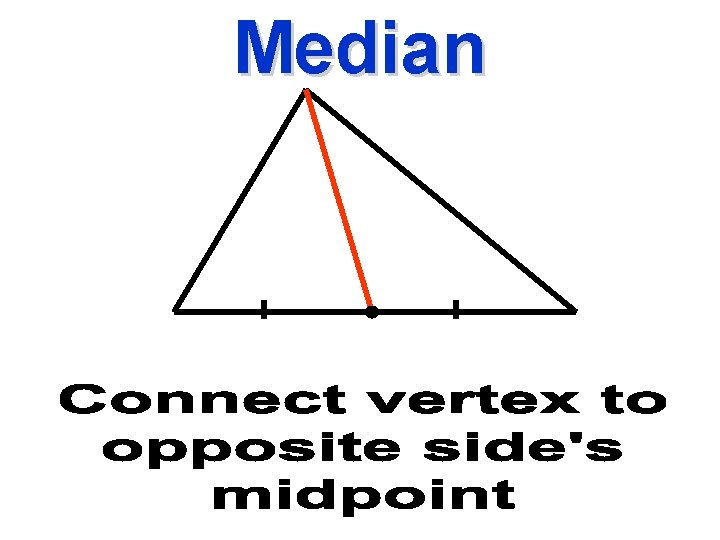
Median

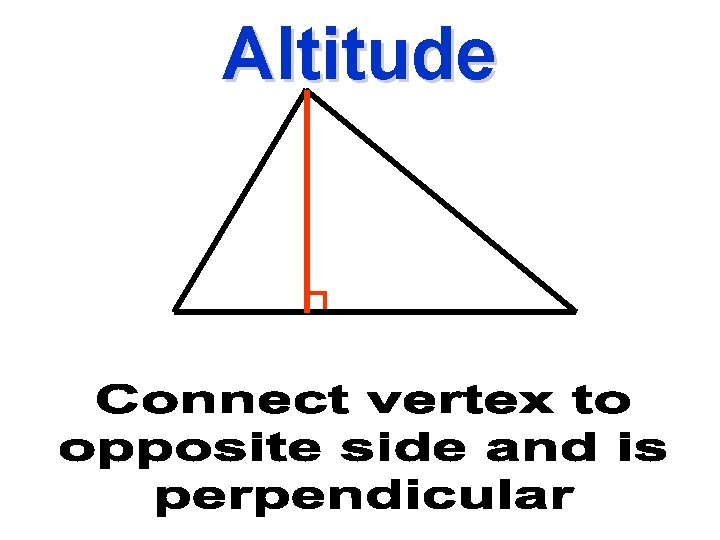
Altitude

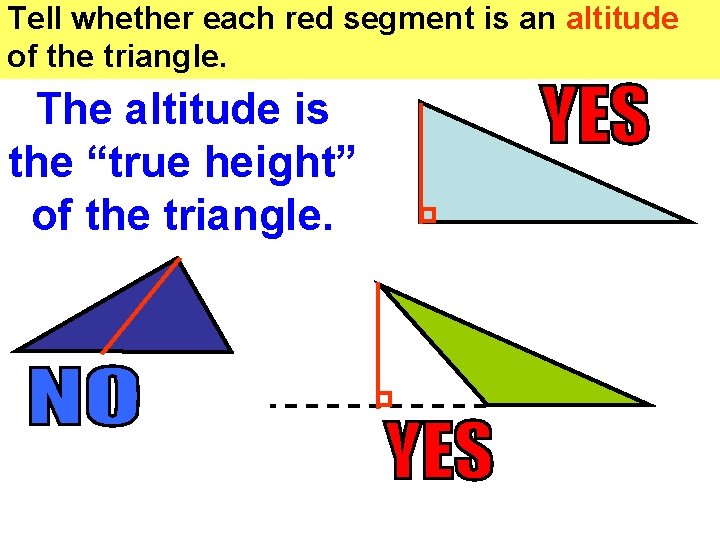
Tell whether each red segment is an altitude of the triangle. The altitude is the “true height” of the triangle.

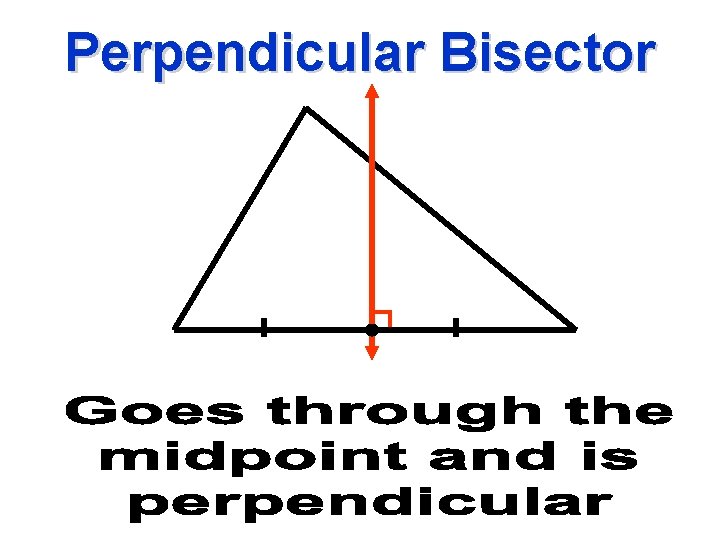
Perpendicular Bisector

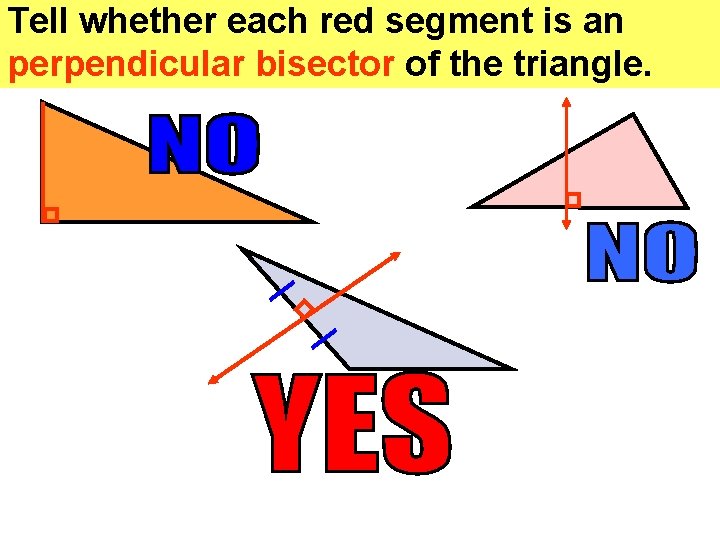
Tell whether each red segment is an perpendicular bisector of the triangle.

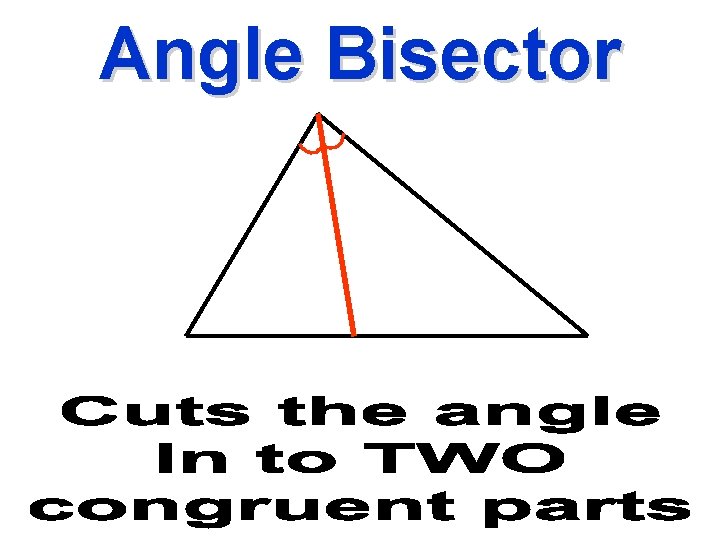
Angle Bisector

Start to memorize… • Indicate the special triangle segment based on its description

I cut an angle into two equal parts

I connect the vertex to the opposite side’s midpoint

I connect the vertex to the opposite side and I’m perpendicular

I go through a side’s midpoint and I am perpendicular

Drill & Practice • Indicate which special triangle segment the red line is based on the picture and markings

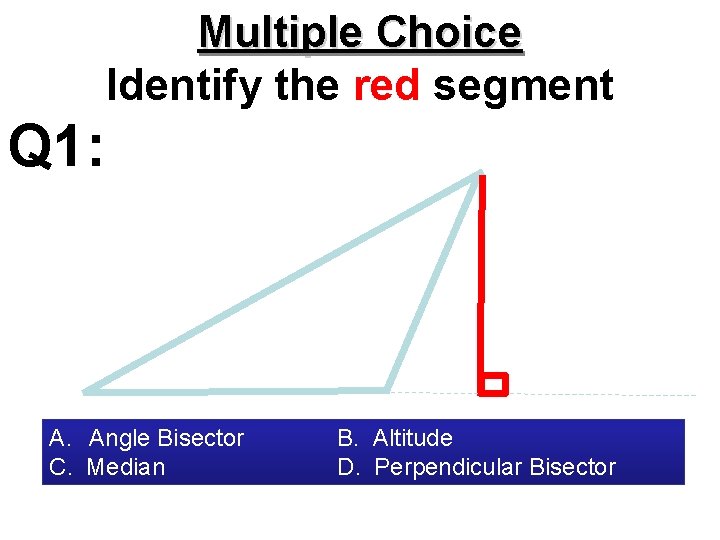
Multiple Choice Identify the red segment Q 1: A. Angle Bisector C. Median B. Altitude D. Perpendicular Bisector

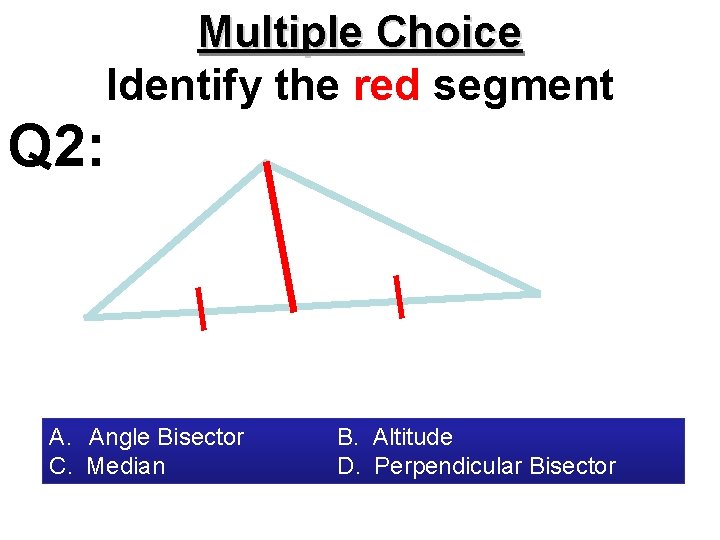
Multiple Choice Identify the red segment Q 2: A. Angle Bisector C. Median B. Altitude D. Perpendicular Bisector

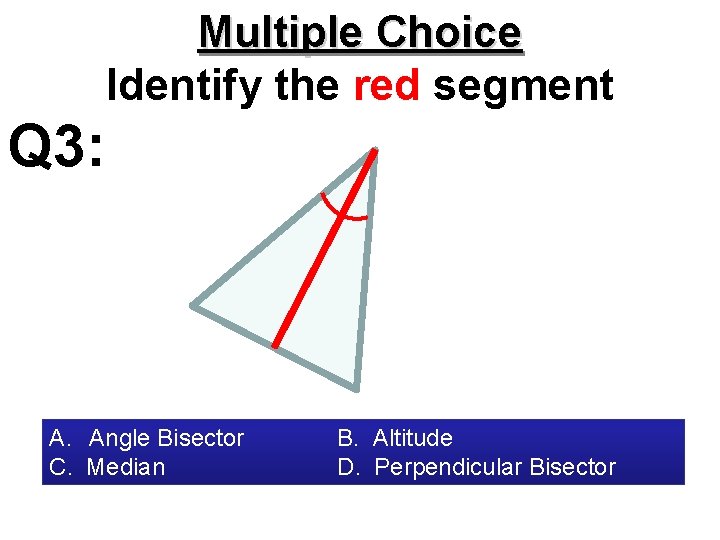
Multiple Choice Identify the red segment Q 3: A. Angle Bisector C. Median B. Altitude D. Perpendicular Bisector

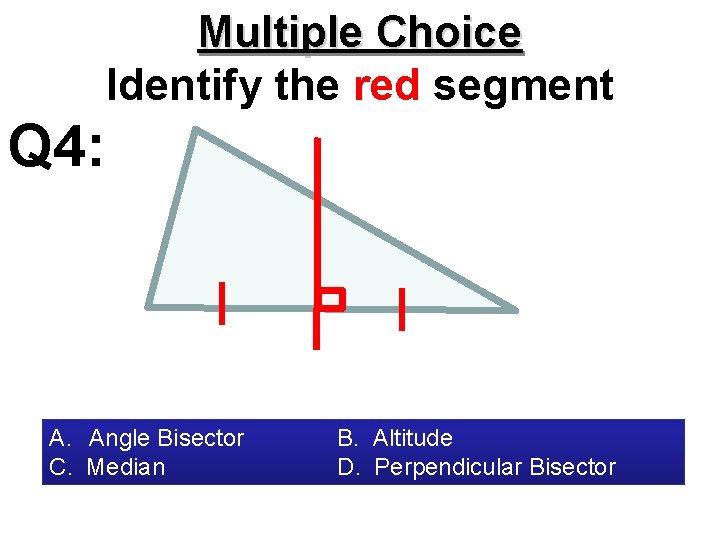
Multiple Choice Identify the red segment Q 4: A. Angle Bisector C. Median B. Altitude D. Perpendicular Bisector

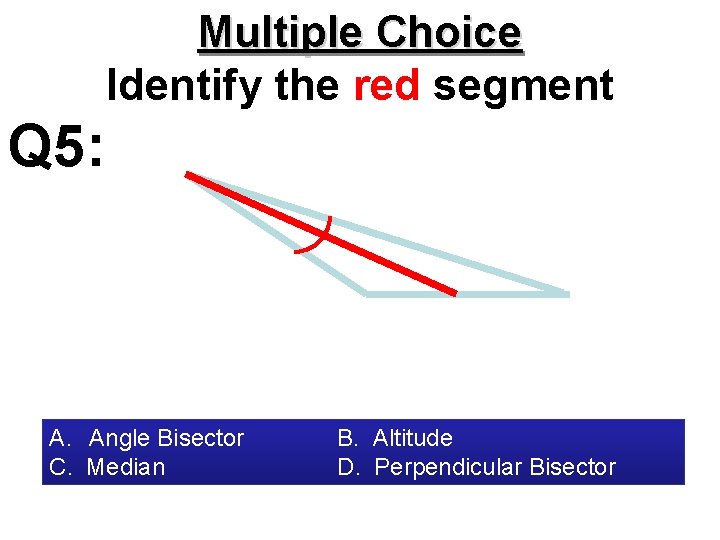
Multiple Choice Identify the red segment Q 5: A. Angle Bisector C. Median B. Altitude D. Perpendicular Bisector

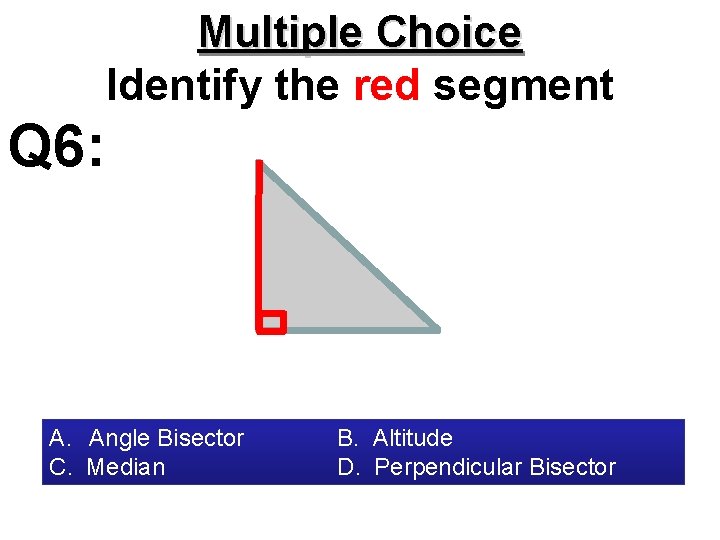
Multiple Choice Identify the red segment Q 6: A. Angle Bisector C. Median B. Altitude D. Perpendicular Bisector

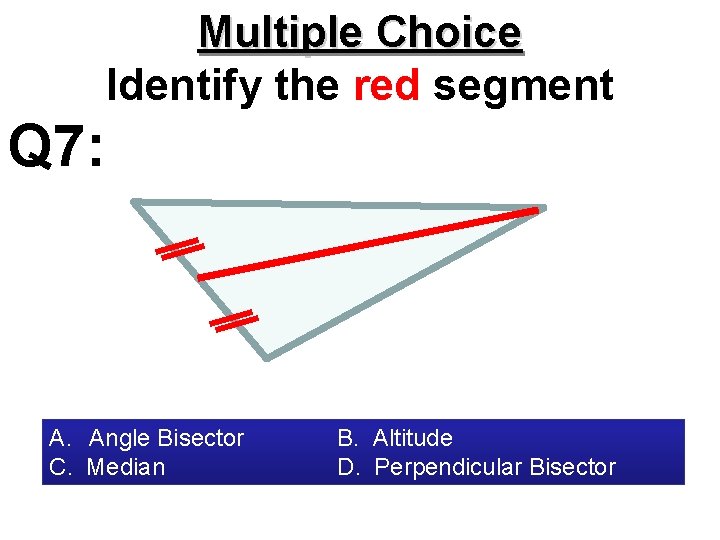
Multiple Choice Identify the red segment Q 7: A. Angle Bisector C. Median B. Altitude D. Perpendicular Bisector

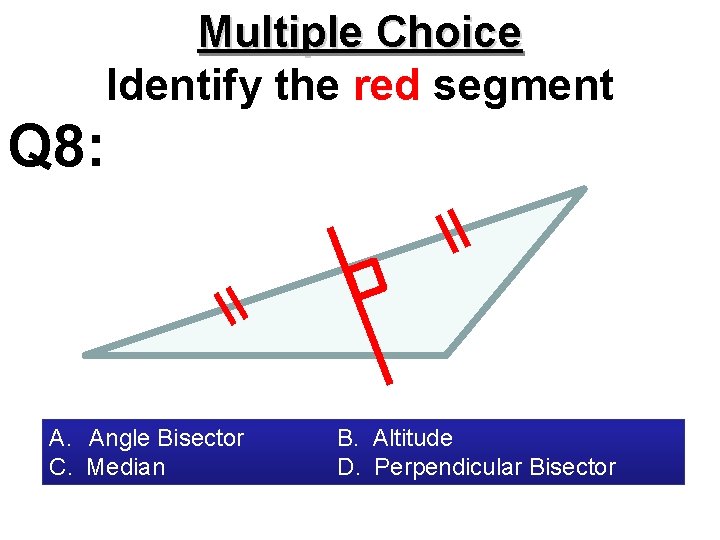
Multiple Choice Identify the red segment Q 8: A. Angle Bisector C. Median B. Altitude D. Perpendicular Bisector

Points of Concurrency

New Vocabulary (Points of Intersection) 1. 2. 3. 4. Centroid Orthocenter Incenter Circumcenter

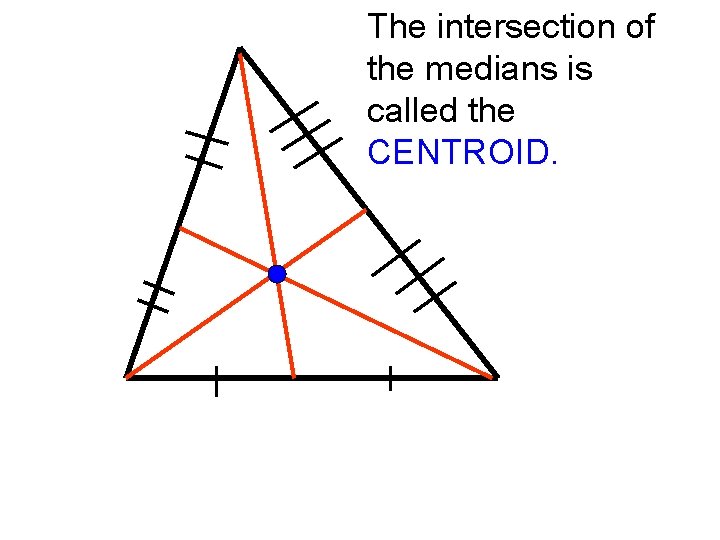
Point of Intersection Medians intersect at the

Important Info about the Centroid • The intersection of the medians. • Found when you draw a segment from one vertex of the triangle to the midpoint of the opposite side. • The center is two-thirds of the distance from each vertex to the midpoint of the opposite side. • Centroid always lies inside the triangle. • This is the point of balance for the triangle.

The intersection of the medians is called the CENTROID.

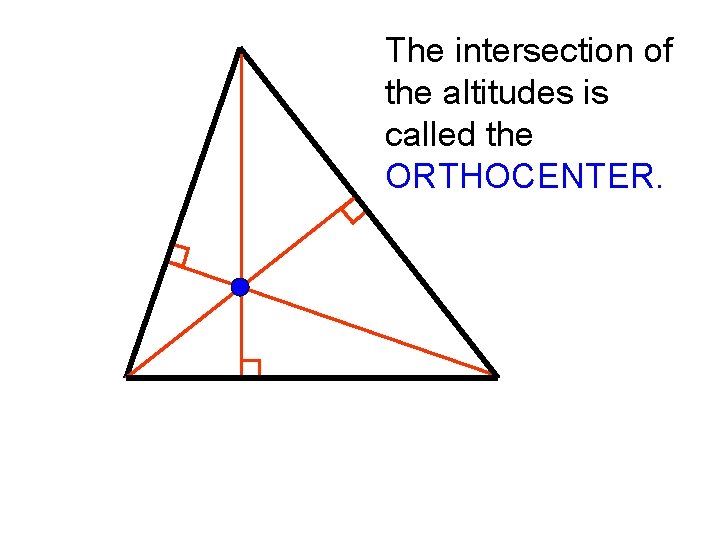
Point of Intersection Altitudes intersect at the

Important Info about the Orthocenter • This is the intersection point of the altitudes. • You find this by drawing the altitudes which is created by a vertex connected to the opposite side so that it is perpendicular to that side. • Orthocenter can lie inside (acute), on (right), or outside (obtuse) of a triangle.

The intersection of the altitudes is called the ORTHOCENTER.

Point of Intersection Angle Bisector intersect at the

Important Info about the Incenter • The angle bisectors of a triangle intersect at a point that is equidistant from the sides of the triangle. • Incenter is equidistant from the sides of the triangle. • The center of the triangle’s inscribed circle. • Incenter always lies inside the triangle

The intersection of the angle bisectors is called the INCENTER.

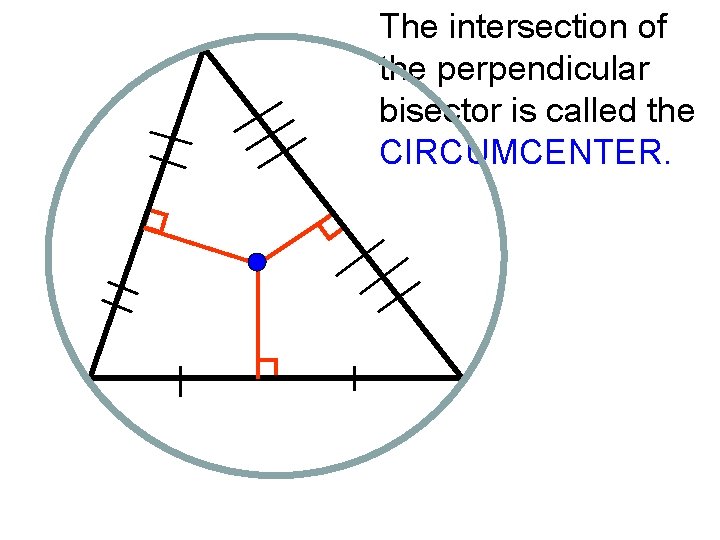
Point of Intersection Perpendicular Bisectors intersect at the

Important Information about the Circumcenter • The perpendicular bisectors of a triangle intersect at a point that is equidistant from the vertices of the triangle. • The circumcenter is the center of a circle that surrounds the triangle touching each vertex. • Can lie inside an acute triangle, on a right triangle, or outside an obtuse triangle.

The intersection of the perpendicular bisector is called the CIRCUMCENTER.

Memorize these! MC AO ABI PBC C Medians/Centroid Altitudes/Orthocenter Angle Bisectors/Incenter Perpendicular Bisectors/Circumcenter

Will this work? MC AO ABI PBC C My Cousin Ate Our Avocados But I Prefer Burritos Covered in Cheese