Warm Up roots Axis of symmetry b 2

Warm Up

= roots Axis of symmetry = -b 2 a x = -(-16) = 1 2(8) y = 8(1)2 – 16(1) -10 = -18 y-intercept a > 0 parabola opens up Axis of symmetry y = 8 x 2 – 16 x -10 a = 8, b = – 16, c = -10 (1, -18) Vertex= minimum

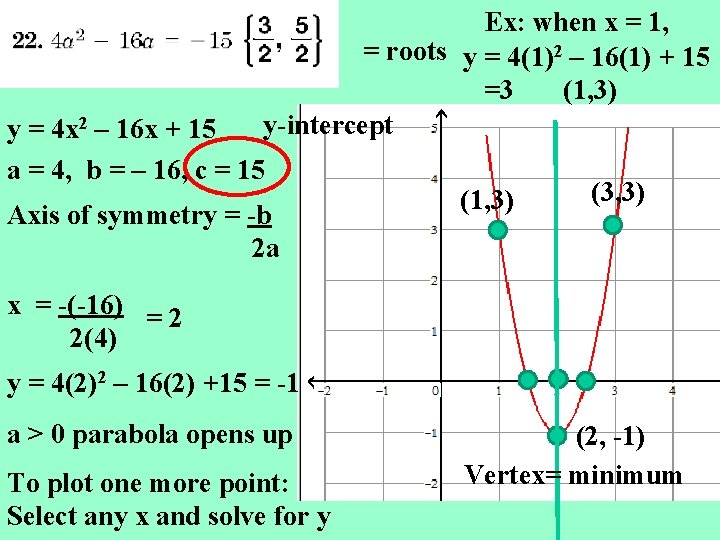
Ex: when x = 1, = roots y = 4(1)2 – 16(1) + 15 =3 (1, 3) y-intercept y = 4 x 2 – 16 x + 15 a = 4, b = – 16, c = 15 Axis of symmetry = -b 2 a (1, 3) (3, 3) x = -(-16) = 2 2(4) y = 4(2)2 – 16(2) +15 = -1 a > 0 parabola opens up To plot one more point: Select any x and solve for y (2, -1) Vertex= minimum

0 = 32 t – 16 t 2

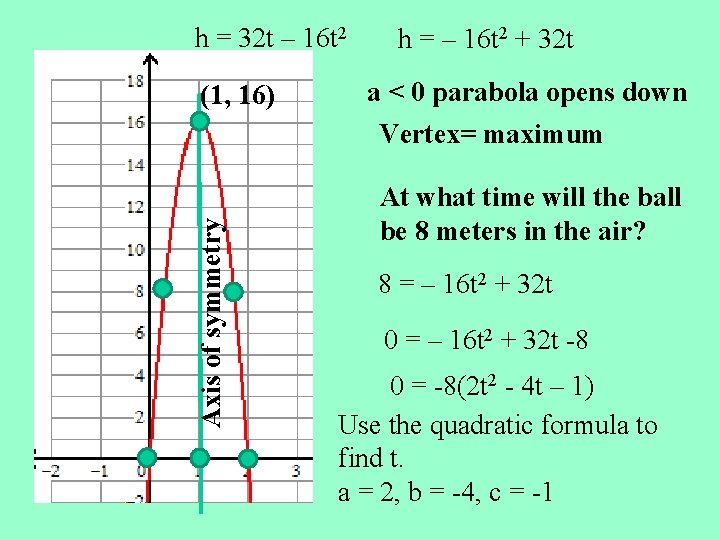
h = 32 t – 16 t 2 (1, 16) h = – 16 t 2 + 32 t a < 0 parabola opens down Axis of symmetry Vertex= maximum At what time will the ball be 8 meters in the air? 8 = – 16 t 2 + 32 t 0 = – 16 t 2 + 32 t -8 0 = -8(2 t 2 - 4 t – 1) Use the quadratic formula to find t. a = 2, b = -4, c = -1

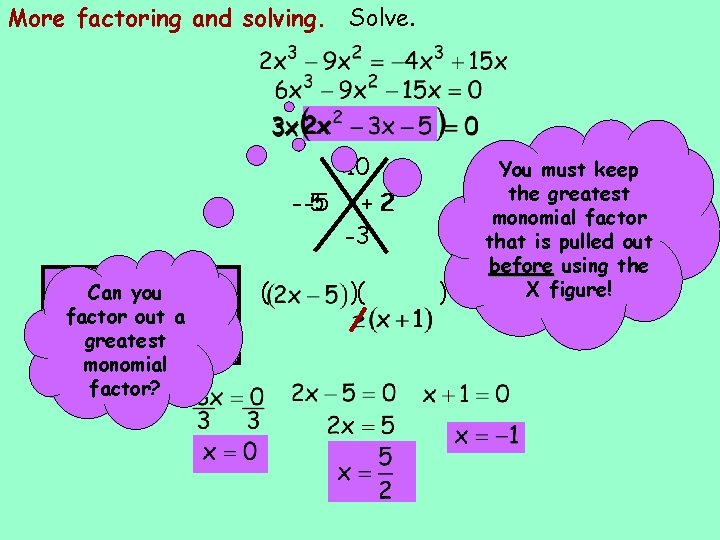
More factoring and solving. Solve. -10 - -5 5 Set. Can theyou factors equal toout zero factor a andgreatest solve. monomial factor? ( +2 -3 )( ) You must keep the greatest monomial factor that is pulled out before using the X figure!

8 -5 Factoring Differences of Squares Algebra 1 Glencoe Mc. Graw-Hill Linda Stamper

Difference of Two Squares factors Recognizing a difference of two squares may help you to factor notice the sum and difference pattern. No middle term – check if first and last terms are squares. Sign is negative. Check using FOIL! product

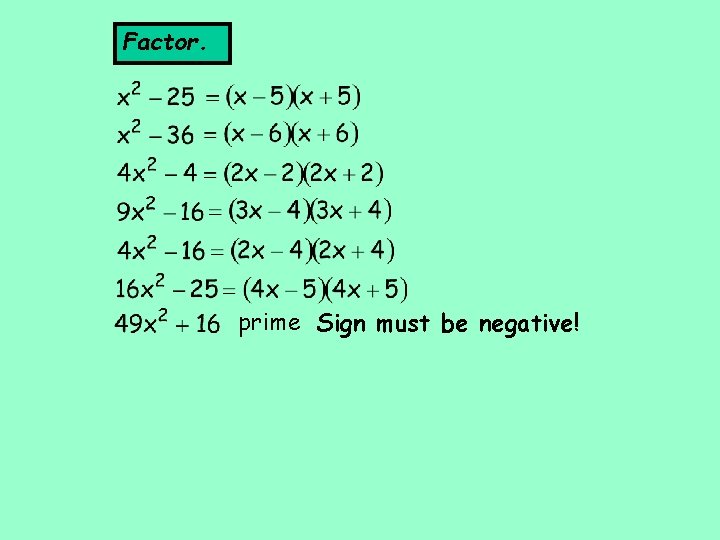
Factor. prime Sign must be negative!

Factor. Example 1 Example 2 Example 3 Example 4 Example 5 Example 6 Check using FOIL!

Remember to factor completely. Write problem. Factor out the GMF. No middle term – check if first and last terms are squares. Factor – must use parentheses. Check using FOIL!

Sometimes you may need to apply several different factoring techniques. The problem. Factor out the GMF. Group terms with common factors. Factor each grouping. Factor the common binomial factor. Factor the difference of squares. Check – Multiply the factors together using FOIL.

Example 7 Example 9 Factor. Example 8 Example 10

Use factoring to solve the equation. Remember to set each factor equal to zero and then solve! Example 11 Example 12 Example 13 Example 14

Use factoring to solve the equation. Remember to set each factor equal to zero and then solve! Example 11 Example 12

Use factoring to solve the equation. Remember to set each factor equal to zero and then solve! Example 13

Use factoring to solve the equation. Remember to set each factor equal to zero and then solve! Example 14

8 -A 11 Pages 451 # 11– 30.