Warm Up n Section 5 1 2 Solving

+ Learning Targets n Extraneous n How Solutions to solve systems of equations using

+ Vocabulary n. Extraneous solution: n Extraneous solution is a solution of the simplified

+ Systems of Equations n. A system of equations is a collection of two

+ Systems of Equations n You are used to solving linear systems of equations.

+ Practice – Equal Value Method (Substitution) n

+ Check answer by graphing: If there is a square root symbol in original

To accurately find the coordinates of the point where two functions intersect, perform the

Select the first function. If the name of one of the intersecting functions does

ü Press ENTER Key. ü Look at the top left hand corner of the

Now use the INTERSECT key to find the answers: There might be more solutions

Finding other possible solutions. In summary, there are three points of intersection: (3, 4)

+ On your own: n. Review your notes. Rewrite and fortify them if needed.

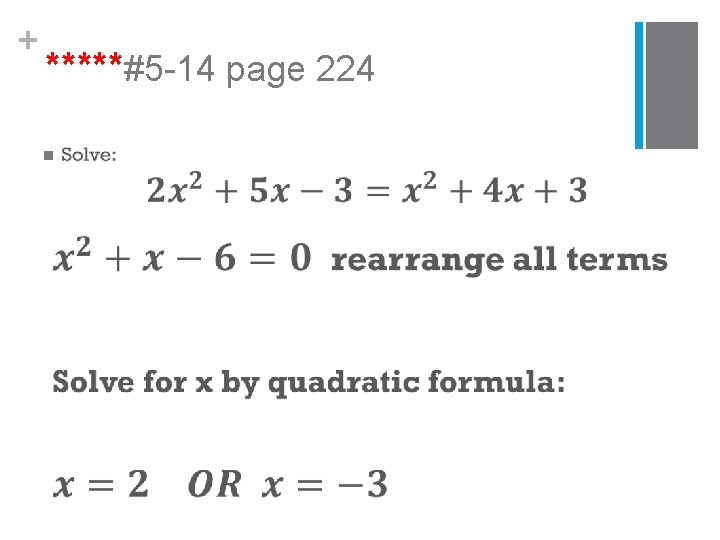
Slides: 26

Download presentation

+ Warm Up!!! n

+ Section 5. 1. 2 Solving Systems

+ Learning Targets n Extraneous n How Solutions to solve systems of equations using technology

+ Non-Linear Example n

+ Check your answer!!! n

+ Vocabulary n. Extraneous solution: n Extraneous solution is a solution of the simplified form of an equation that does not satisfy the original equation. n Watch out for extraneous solutions, they show up when the variable is under a radical sign or when the variable is in the denominator of a fraction.

+ Systems of Equations n. A system of equations is a collection of two or more equations with a same set of variables. n In solving a system of equations, we try to find values for each of the variables that will satisfy every equation in the system. n The equations in the system can be linear or nonlinear.

+ Systems of Equations n You are used to solving linear systems of equations. n There are three common methods used to solve systems of linear equations. They are, in no particular order: 1) Elimination 2) Equal Value Method (Substitution) 3) Graphing

+ Practice - Elimination n

+ Practice – Equal Value Method (Substitution) n

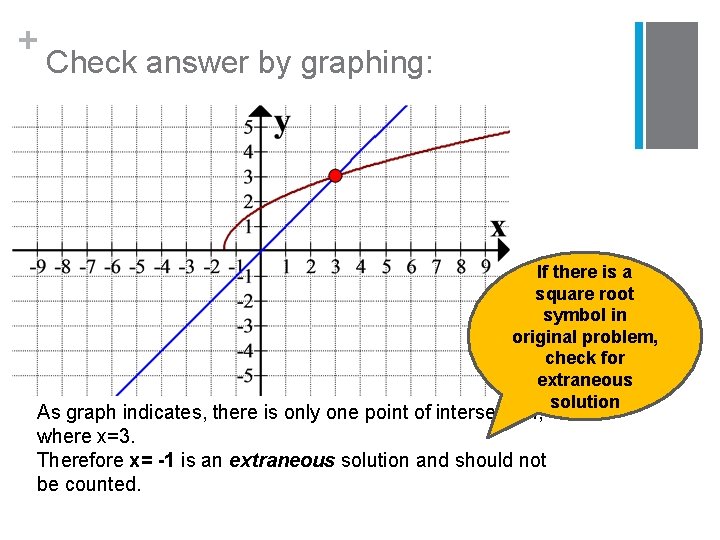
+ Check answer by graphing: If there is a square root symbol in original problem, check for extraneous solution As graph indicates, there is only one point of intersection, where x=3. Therefore x= -1 is an extraneous solution and should not be counted.

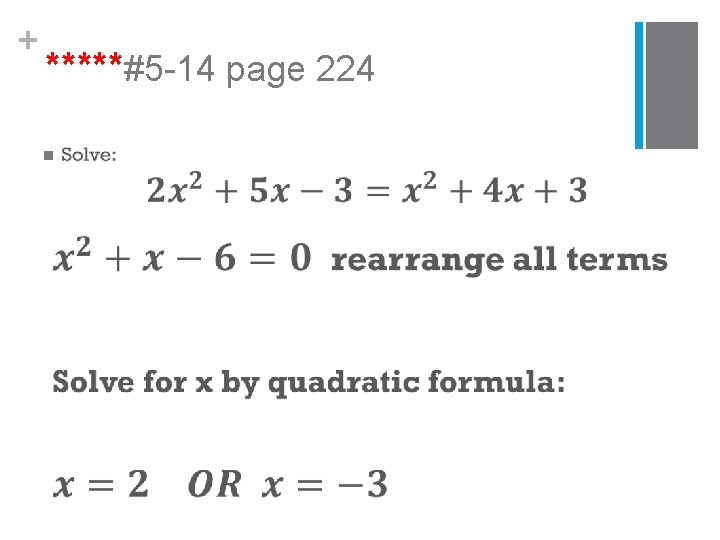
+ *****#5 -14 page 224 n

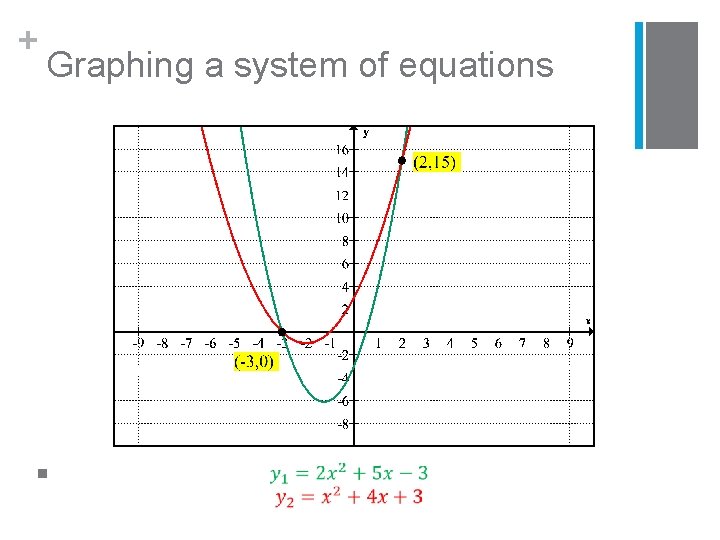
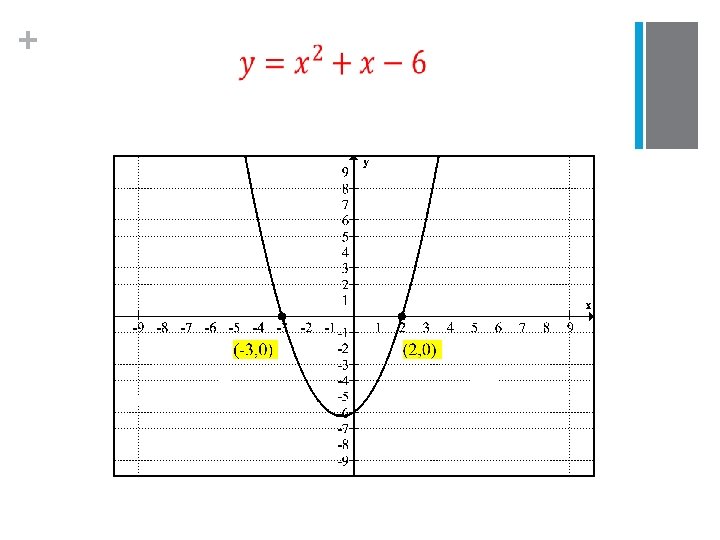
+ Graphing a system of equations n

+ #5 -15 Modified! n

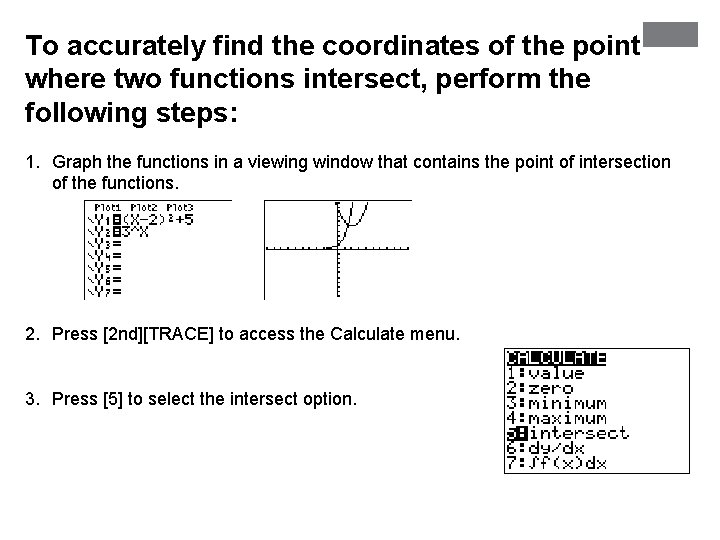
To accurately find the coordinates of the point where two functions intersect, perform the following steps: 1. Graph the functions in a viewing window that contains the point of intersection of the functions. 2. Press [2 nd][TRACE] to access the Calculate menu. 3. Press [5] to select the intersect option.

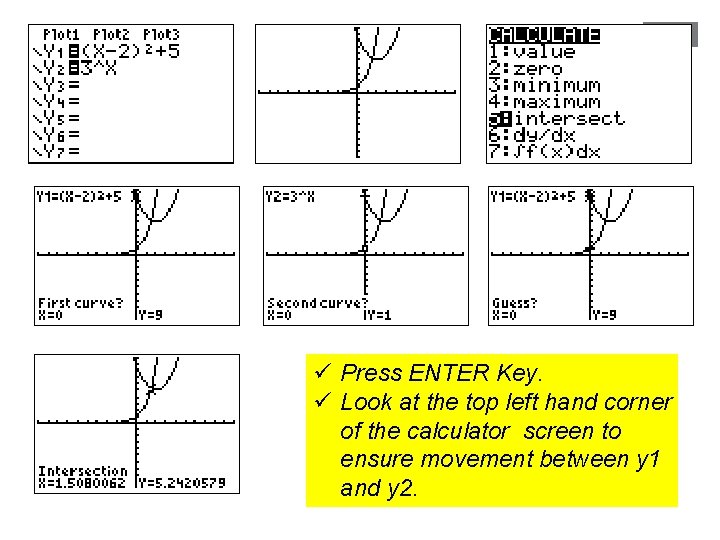
Select the first function. If the name of one of the intersecting functions does not appear at the top of the screen, repeatedly press Select the second function. If the calculator does not automatically display the name of the second intersecting function at the top of the screen, repeatedly press arrow key. The next slide summarizes all the steps

ü Press ENTER Key. ü Look at the top left hand corner of the calculator screen to ensure movement between y 1 and y 2.

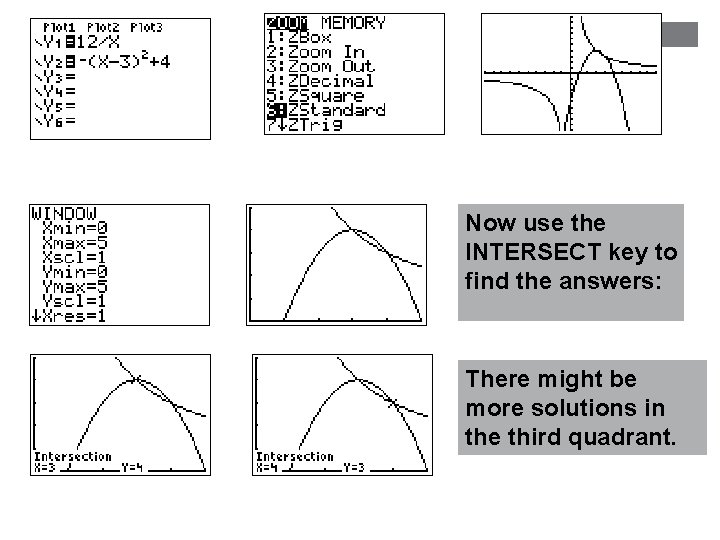
+ #5 -16 n

Now use the INTERSECT key to find the answers: There might be more solutions in the third quadrant.

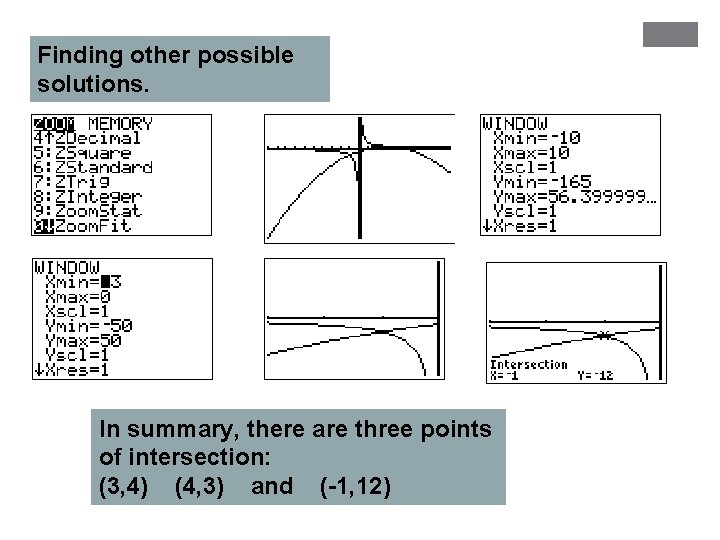
Finding other possible solutions. In summary, there are three points of intersection: (3, 4) (4, 3) and (-1, 12)

+ Practice n

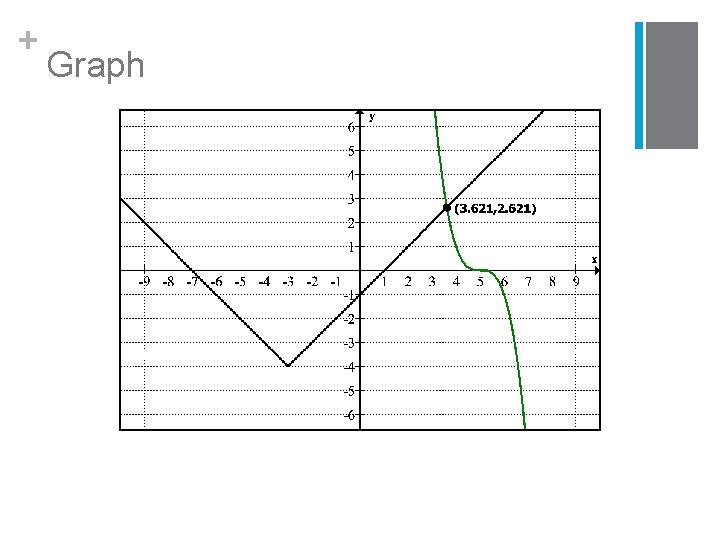
+ Graph

+ On your own: n. Review your notes. Rewrite and fortify them if needed. n. Update your vocab list, if needed. n Review and Preview n Page n# 226 18 -21, 23 -25, 27 and 28