Warm up Multiply then write in standard form

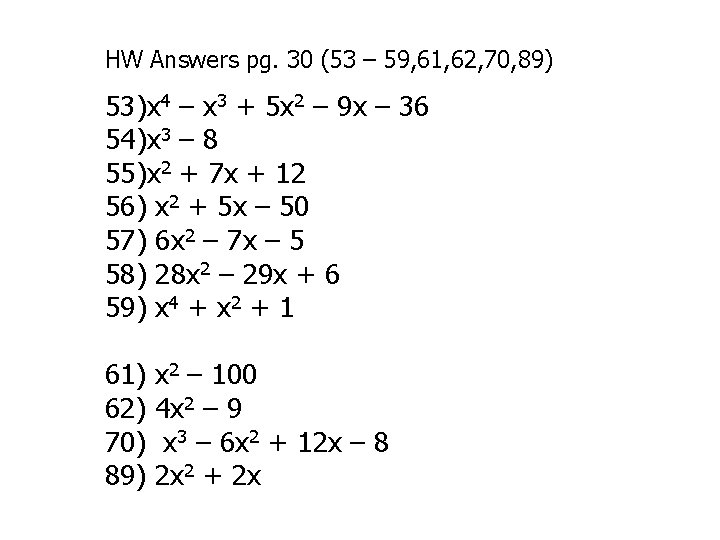








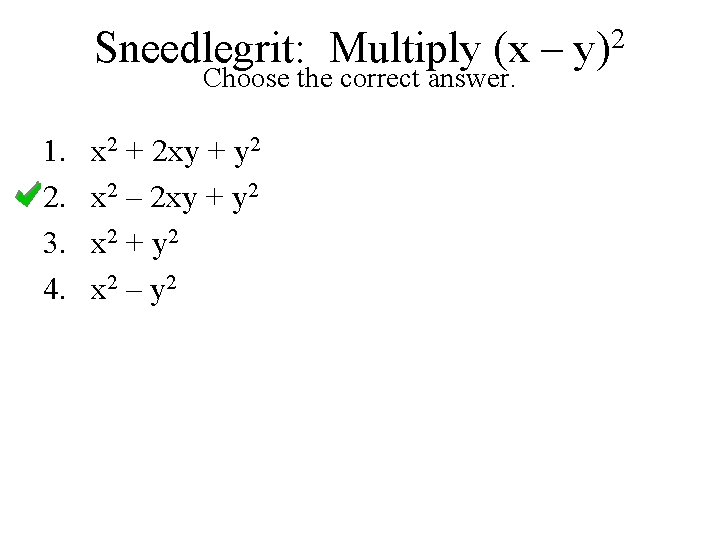

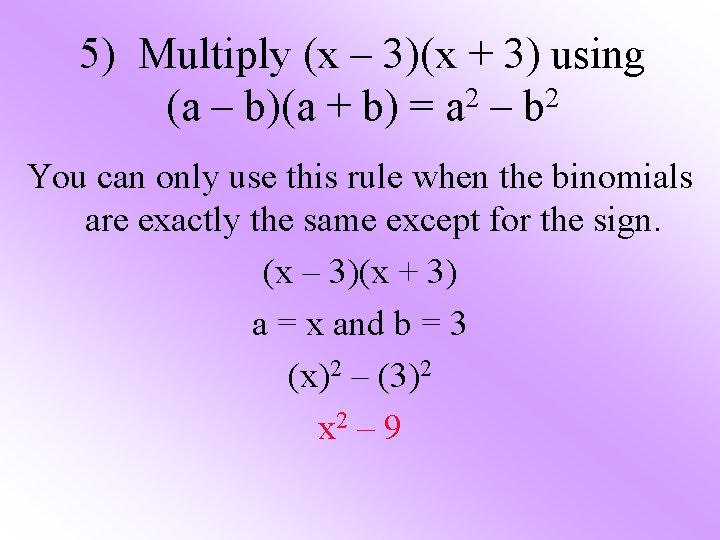
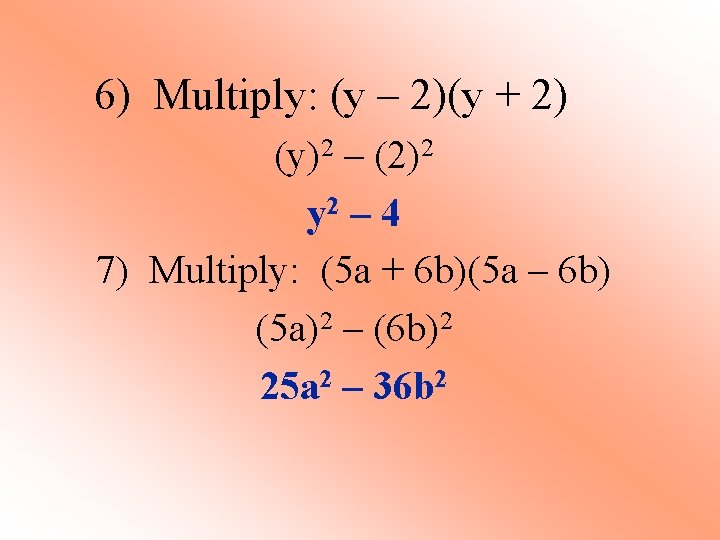


- Slides: 16

Warm up: Multiply, then write in standard form: 1) (x + 3)(x – 5) 2) (x + 3)(3 x 2 – 4 x + 1)
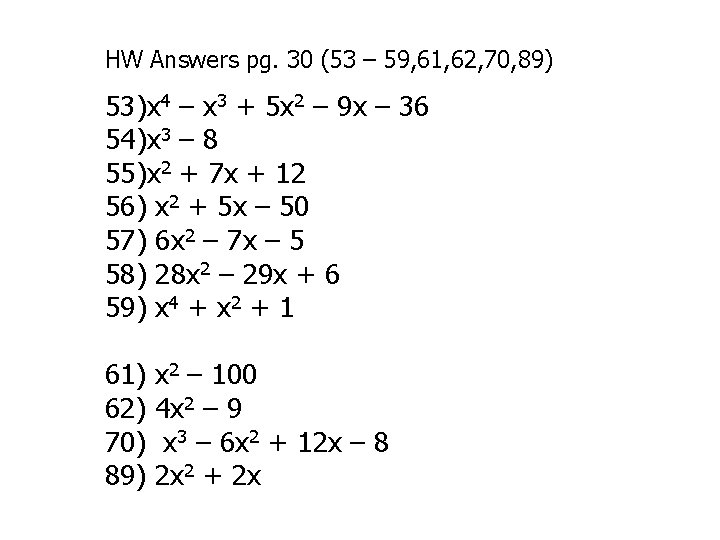
HW Answers pg. 30 (53 – 59, 61, 62, 70, 89) 53)x 4 – x 3 + 5 x 2 – 9 x – 36 54)x 3 – 8 55)x 2 + 7 x + 12 56) x 2 + 5 x – 50 57) 6 x 2 – 7 x – 5 58) 28 x 2 – 29 x + 6 59) x 4 + x 2 + 1 61) 62) 70) 89) x 2 – 100 4 x 2 – 9 x 3 – 6 x 2 + 12 x – 8 2 x 2 + 2 x

Objective The student will be able to: use patterns to multiply special binomials.

There are formulas (shortcuts) that work for certain polynomial multiplication problems. Square of a Binomial: (a + b)2 = a 2 + 2 ab + b 2 2 (a – b) = a – 2 ab + b Sum and Difference of Same Terms (a - b)(a + b) = 2 a - 2 b Being able to use these formulas will help you in the future when you have to factor. If you do not remember the formulas, you can always multiply using distributive, FOIL, or the box method.

Let’s try one! 1) Multiply: (x + 4)2 You can multiply this by rewriting this as (x + 4) OR You can use the following rule as a shortcut: (a + b)2 = a 2 + 2 ab + b 2 For comparison, I’ll show you both ways.

1) Multiply (x + 4) First terms: x 2 Outer terms: +4 x Inner terms: +4 x Last terms: +16 Combine like terms. x 2 +8 x + 16 Notice you have two of the same answer? x x +4 x 2 +4 x +4 +4 x +16 Now let’s do it with the shortcut!

1) Multiply: (x + 4)2 That’s why the 2 is in the formula! using (a + b)2 = a 2 + 2 ab + b 2 a is the first term, b is the second term (x + 4)2 a = x and b = 4 Plug into the formula a 2 + 2 ab + b 2 (x)2 + 2(x)(4) + (4)2 This is the Simplify. same answer! x 2 + 8 x+ 16

2) Multiply: (3 x + 2 y)2 using (a + b)2 = a 2 + 2 ab + b 2 (3 x + 2 y)2 a = 3 x and b = 2 y Plug into the formula a 2 + 2 ab + b 2 (3 x)2 + 2(3 x)(2 y) + (2 y)2 Simplify 9 x 2 + 12 xy +4 y 2

Sneedlegrit: Multiply (2 a + 3)2 Choose the correct answer. 1. 2. 3. 4. 4 a 2 – 9 4 a 2 + 36 a + 9 4 a 2 + 12 a + 9

Multiply: (x – 5)2 using (a – b)2 = a 2 – 2 ab + b 2 Everything is the same except the signs! (x)2 – 2(x)(5) + (5)2 x 2 – 10 x + 25 4) Multiply: (4 x – y)2 (4 x)2 – 2(4 x)(y) + (y)2 16 x 2 – 8 xy + y 2
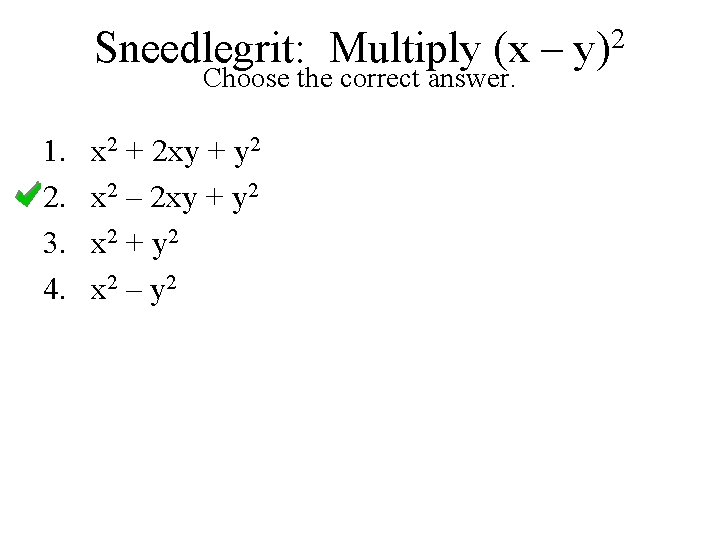
Sneedlegrit: Multiply (x – y)2 Choose the correct answer. 1. 2. 3. 4. x 2 + 2 xy + y 2 x 2 – y 2

5) Multiply (x – 3)(x + 3) First terms: x 2 Outer terms: +3 x Inner terms: -3 x Last terms: -9 Combine like terms. x 2 – 9 Notice the middle terms eliminate each other! x -3 x 2 -3 x +3 +3 x -9 x This is called the difference of squares.
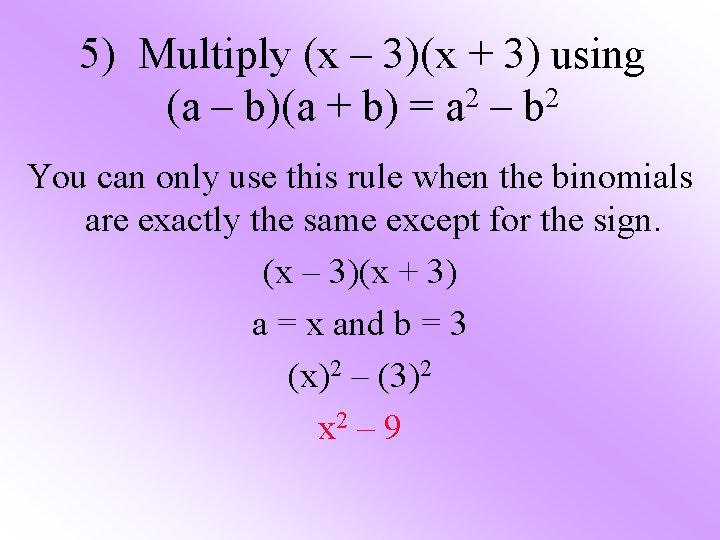
5) Multiply (x – 3)(x + 3) using 2 2 (a – b)(a + b) = a – b You can only use this rule when the binomials are exactly the same except for the sign. (x – 3)(x + 3) a = x and b = 3 (x)2 – (3)2 x 2 – 9
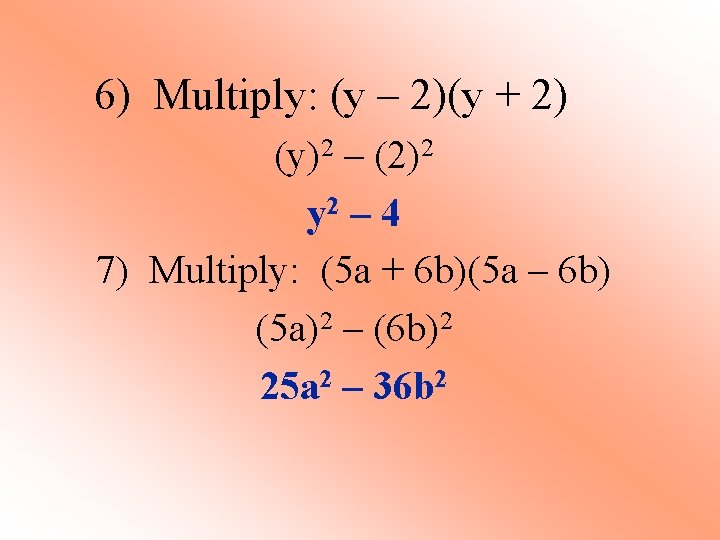
6) Multiply: (y – 2)(y + 2) (y)2 – (2)2 y 2 – 4 7) Multiply: (5 a + 6 b)(5 a – 6 b) (5 a)2 – (6 b)2 25 a 2 – 36 b 2

Sneedlegrit: Multiply (4 m – 3 n)(4 m + 3 n) Choose the correct answer. 1. 2. 3. 4. 16 m 2 – 9 n 2 16 m 2 + 9 n 2 16 m 2 – 24 mn - 9 n 2 16 m 2 + 24 mn + 9 n 2

Summary: • Sum and difference of same terms • Square of a binomial Sneedlegrits: Multiply each and write in standard form. 1) (2 x – 7)(2 x + 7) 2) (3 x – 4)2 HW: pg. 30 (63 – 69, 71 -74, 82, 91)