Warm up honors algebra 2 3719 Pick up

Warm up honors algebra 2 3/7/19 Pick up the handout by the projector and begin working on it “Exponential Practice” Applying same base exponentials

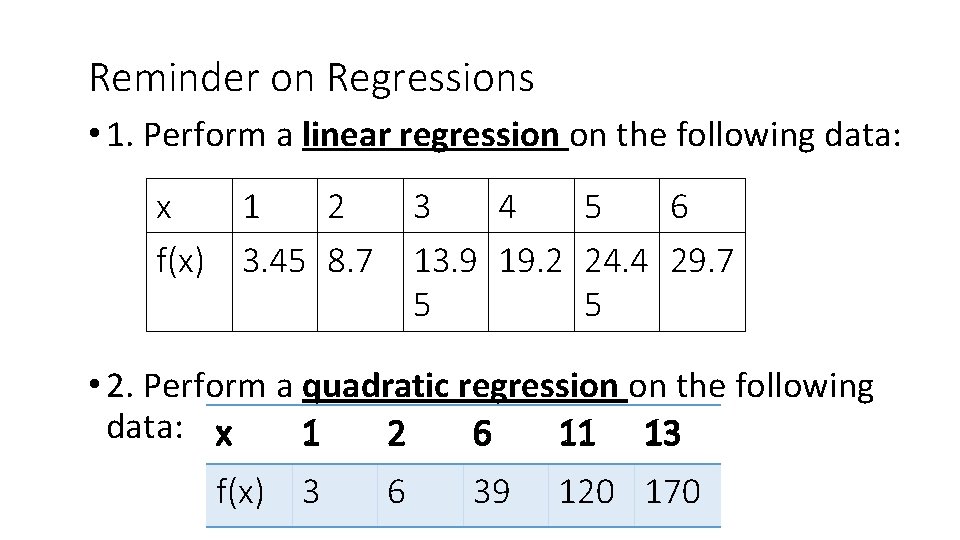
Reminder on Regressions • 1. Perform a linear regression on the following data: x f(x) 1 2 3. 45 8. 7 3 4 5 6 13. 9 19. 2 24. 4 29. 7 5 5 • 2. Perform a quadratic regression on the following data: x 1 2 6 11 13 f(x) 3 6 39 120 170

Calculator reminder!! • How to find the curve of best fit when given a data table: 1. Enter data into table on calculator STAT EDIT (1) x-values in L 1 yvalues in L 2 2. Determine the type of function the data represents • - Linear, Quadratic or Exponential

Calculator reminder (cont): 3. STAT tab over to CALC select type of function Enter through 4: Lin. Reg(ax+b) (linear) 5: Quad. Reg (Quadratic) 0: Exp. Reg (Exponential) 9: Ln. Reg (Natural Log) 4. Plug the given values into the function formula.

Curve of best fit = Regression • Examples: o“Find the curve of best fit for this linear data” = “Perform a linear regression” o“Perform a quadratic regression” = “Find the curve of best fit”

Linear functions (first degree) • First differences are constant!! x f(x) First Differences: -1 2 0 5 +3 1 8 +3 2 11 +3 First differences are constant, so linear function!!

Quadratic functions (Second Degree) • Second differences are constant!! x -1 0 1 2 f(x) 2 3 5 8 First Differences: Second Differences: +1 +2 +1 +3 +1 First differences are NOT constant!! NOT Linear!! Second differences are constant, so Quadratic!!

Exponential functions • Ratio of y-values are constant!! x -1 0 1 2 f(x) 16 24 36 54 First Differences: Second Differences: Ratios: +8 +12 +4 +6 First differences are NOT constant!! NOT Linear!! Second differences are NOT constant!! NOT Quadratic!! Ratios are constant, so Exponential!!

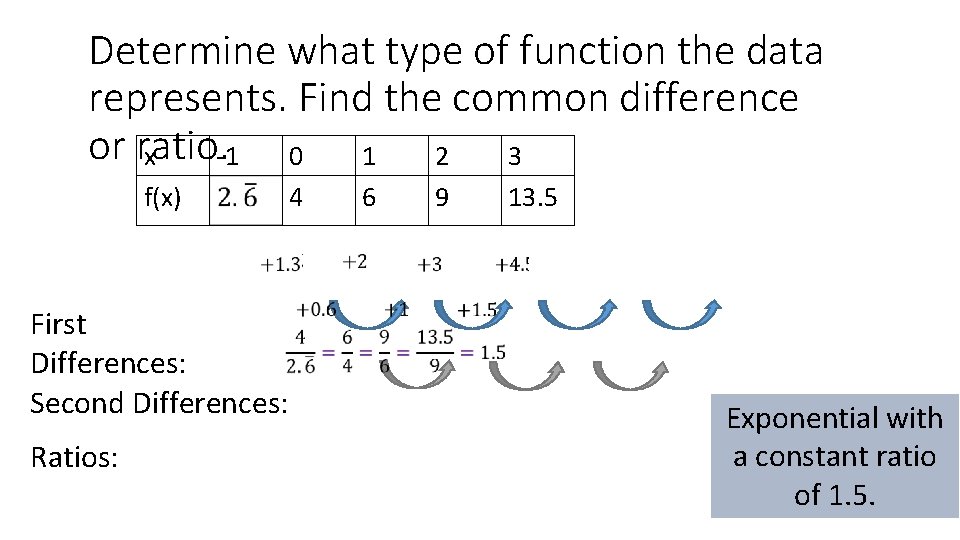
Determine what type of function the data represents. Find the common difference or ratio. x -1 0 1 2 3 f(x) First Differences: Second Differences: Ratios: 4 6 9 13. 5 Exponential with a constant ratio of 1. 5.

Determine what type of function the data represents. Find the common difference or ratio. x -1 0 1 2 3 f(x) First Differences: 2 7 12 17 Linear with a first common difference of 5.

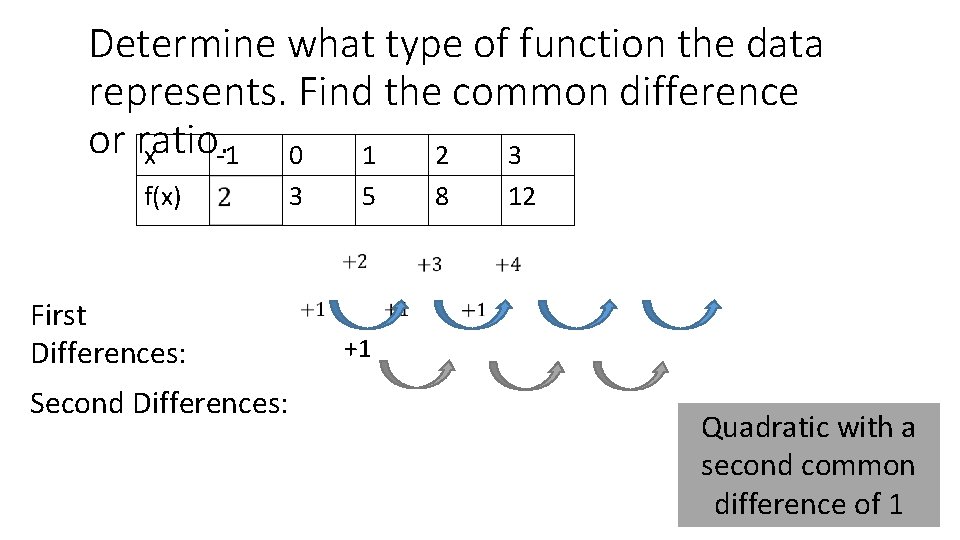
Determine what type of function the data represents. Find the common difference or ratio. x -1 0 1 2 3 f(x) First Differences: Second Differences: 3 5 8 12 +1 Quadratic with a second common difference of 1

Find an exponential model for the data. Use the model to predict when the tuition at U. T. Austin will be $6000. Year Tuition 1999 -00 $3128 2000 -01 $3585 2001 -02 $3776 2002 -03 $3950 2003 -04 $4188 Enter data in the graphing calculator and use the exponential regression feature (0)

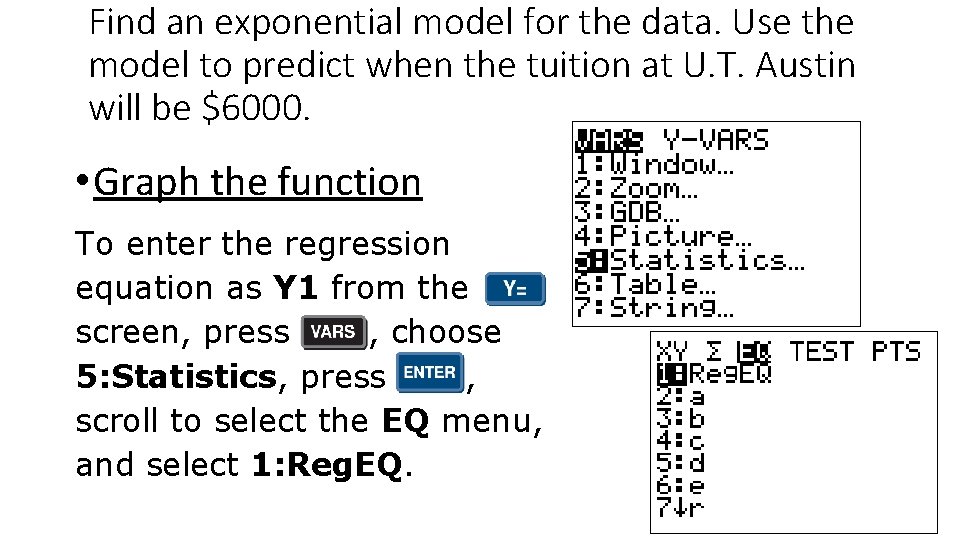
Find an exponential model for the data. Use the model to predict when the tuition at U. T. Austin will be $6000. • Graph the function To enter the regression equation as Y 1 from the screen, press , choose 5: Statistics, press , scroll to select the EQ menu, and select 1: Reg. EQ.

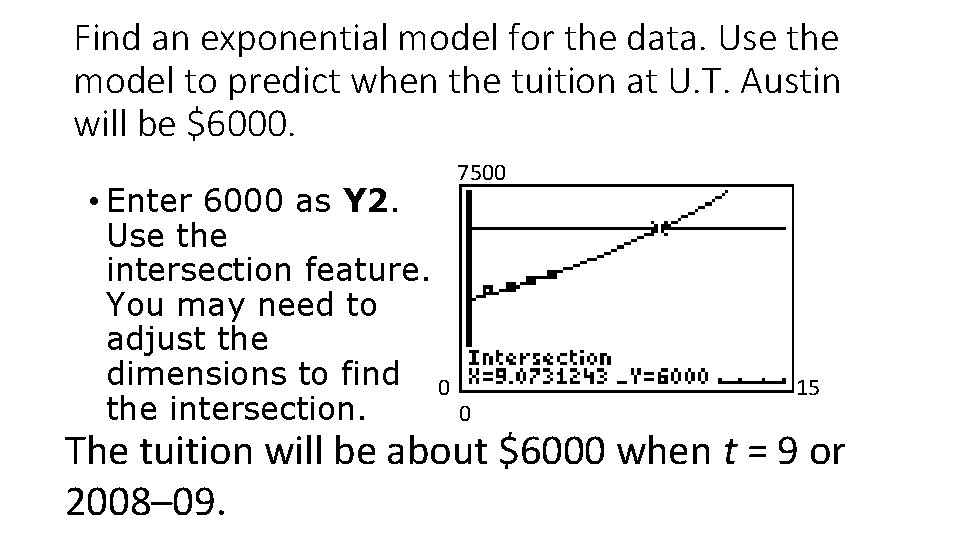
Find an exponential model for the data. Use the model to predict when the tuition at U. T. Austin will be $6000. 7500 • Enter 6000 as Y 2. Use the intersection feature. You may need to adjust the dimensions to find 0 the intersection. 0 15 The tuition will be about $6000 when t = 9 or 2008– 09.

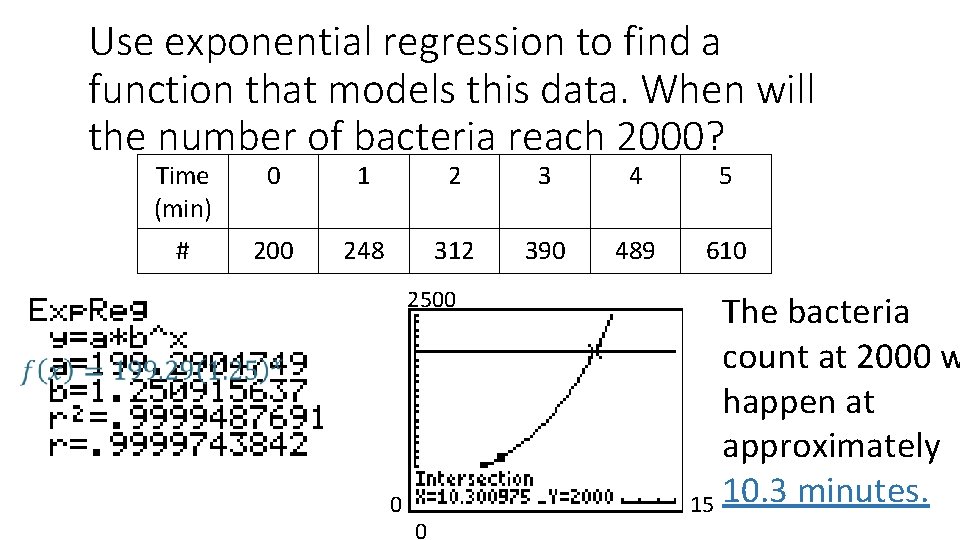
Use exponential regression to find a function that models this data. When will the number of bacteria reach 2000? Time (min) 0 1 2 3 4 5 # 200 248 312 390 489 610 2500 0 0 The bacteria count at 2000 w happen at approximately 15 10. 3 minutes.

Find a natural log model for the data. According to the model, when will the global population exceed 9, 000, 000? Global Population Growth Population (billions) Year 1 1800 2 1927 3 1960 4 1974 5 1987 6 1999 The population will exceed 9, 000, 000 (x=9) in the year 2058.

Use the logarithmic regression to find a function that models this data. When will the speed reach 8. 0 m/s? Time (min) 1 2 3 4 5 6 7 Speed (m/s) 0. 5 2. 5 3. 5 4. 3 4. 9 5. 3 5. 6 Use the intersect feature to find y when x is 8. The time it will reach 8. 0 m/s is 16. 6 min.