Warm Up Describe the pattern and sketch the
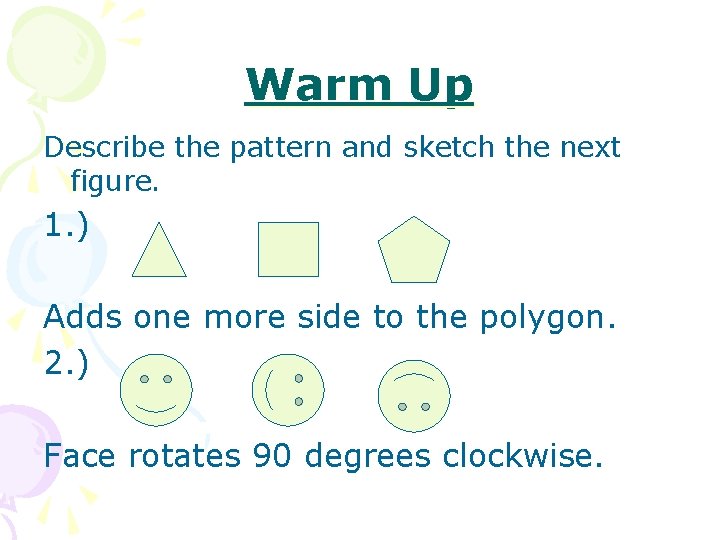
Warm Up Describe the pattern and sketch the next figure. 1. ) Adds one more side to the polygon. 2. ) Face rotates 90 degrees clockwise.

Geometry Sections 2. 1, 2. 2 Use Inductive Reasoning and Analyze Conditional Statements

Describe a Number Pattern Describe the pattern in the numbers and find the next number in the sequence. 1. ) 3, 6, 12, 24, 48 Multiply by 2 2. ) 0, 1, 4, 9, 16, 25, 36 Perfect squares

Vocabulary • Conjecture: An unproven statement that is based on observations. • You use inductive reasoning when you find a pattern in specific cases and then write a conjecture for the general case.

Conjecture/ Counterexamples • Use these sums of odd integers: 3+7=10, 1+7=8, 17+21=38 Conjecture: The sum of any two odd integers is__ even _______.

Vocabulary • Counterexample: An example that proves a conjecture is false. *Example: • Conjecture: The sum of two numbers is always greater than the larger number. Counterexample: -3 + -2 = -5

Conjecture/ Counterexamples • Show the conjecture is false by finding a counterexample. – If the product of two numbers is positive, then the two numbers must both be positive. -8 * -2 = 16

Vocabulary Conditional statement: a logical statement that has two parts, a hypothesis and a conclusion. When a conditional statement is written in if-then form the “if” part contains the hypothesis and the “then” part contains the conclusion. If hypothesis, then conclusion.

Conditional Statements Rewrite statement in if-then form: Guitar players are musicians If you are a guitar player then you are a musician.

Conditional Statement Rewrite the statement in if-then form: An even number is divisible by two. If a number is even, then it is divisible by two.

Converse The converse of a conditional statement is formed by switching the conclusion and the hypothesis. Conditional Statement: If you are a guitar player then you are a musician. Converse: If you are a musician then you are a guitar player.

Converse Example Write the converse of: If a number is even, then it is divisible by two. Converse: If a number is divisible by two, then it is an even number.

Inverse The inverse of a conditional statement is when you negate the hypothesis and the conclusion. (Turn them into nots) Conditional Statement: If you are a guitar player then you are a musician. Inverse: If you are not a guitar player than you are not a musician.

Inverse Example Write the Inverse of: If a number is even, then it is divisible by two. Inverse: If a number is not even, then it is not divisible by two.

Contrapositive The contrapositive of a conditional statement is when you negate the hypothesis and conclusion of the converse statement. Converse Statement: If you are a musician, then you are a guitar player. Contrapositive: If you are not a musician, then you are not a guitar player

Contrapositive Example Write the contrapositive of: If a number is divisible by two, then it is an even number. Contrapositive: If a number is not divisible by two, then it is not an even number.

Related Conditionals • Conditional statement: If hypothesis, then conclusion. • Inverse: If not hypothesis, then not conclusion. • Converse: If conclusion, then hypothesis. • Contrapositive: If not conclusion, then not hypothesis.

Write the inverse, converse, & contrapositive. • Conditional: If water is frozen, then its temp is below zero. • Inverse: If water is not frozen, then its temp is not below zero. • Converse: If the temp is below zero, then water is frozen. • Contrapositive: If the temp is not below zero, then the water is not frozen.

Homework: • Page 67 - 68 • #6 -10(evens), 16, 17 • Page 74 • #3 -6
- Slides: 19