Warm Up 2 Trig Review Power Rule Review



















- Slides: 22

Warm Up #2: Trig Review, Power Rule Review AND pg 139 #40 -45 AND pg 146 #51 • AND remember sin²(x) + cos²(x) = 1

Review #11 on hw (a) When does the body reverse direction? (b) When (approximately) is the body moving at a constant speed? (c) Graph the body’s speed for 0, 10 (d) Graph the acceleration, where defined.

CH 3. 5 Derivatives of Trigonometric Functions

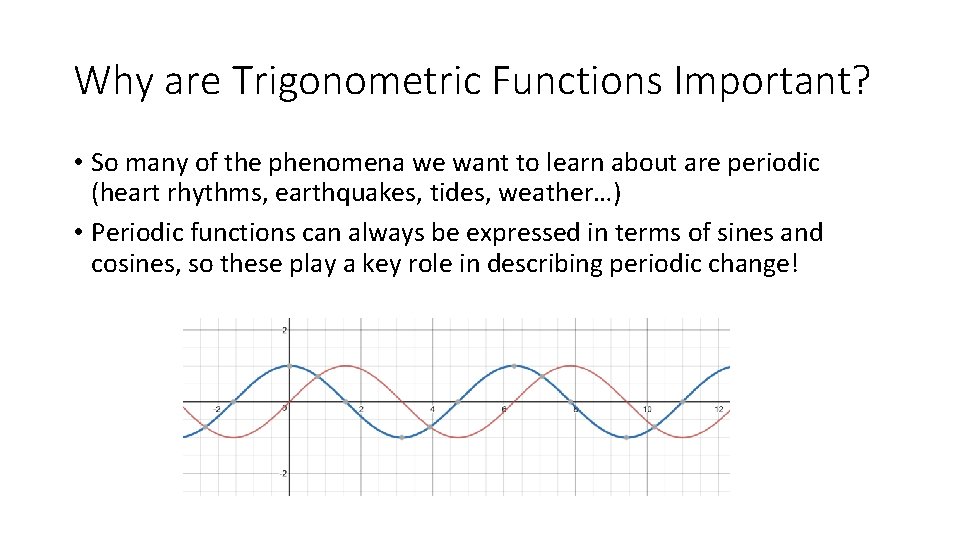
Why are Trigonometric Functions Important? • So many of the phenomena we want to learn about are periodic (heart rhythms, earthquakes, tides, weather…) • Periodic functions can always be expressed in terms of sines and cosines, so these play a key role in describing periodic change!

Review: Pre. Calc Double Angle Formulas sin(A+B) = sin A cos B + cos A sin B sin(A−B) = sin A cos B − cos A sin B cos(A+B) = cos A cos B − sin A sin B cos(A−B) = cos A cos B + sin A sin B tan(A+B) = (tan A + tan B) / (1 − tan A tan B) tan(A−B) = (tan A − tan B) / (1 + tan A tan B)

What is the derivative of the sine function? •

What is the derivative of each of the 6 trigonometric functions? •

EX 1: Using the Differentiation Rules •

EX 2: A Trig Second Derivative a) Find y” if y = sec(x) b) Find y’’ if y = 7 sin(x) + 1

You Try! •

What is jerk? •

EX 3: A Couple of Jerks •

EX 4: Applications of Trig - The motion of a Weight on a Spring •

You Try! •

EX 5: Finding Tangent and Normal Lines •

You Try! •

How do we calculate derivatives on a calculator? Our graphing calculator uses the symmetric difference quotient to calculate the numerical derivative of f at a point a, abbreviated as NDER f(a). (sometimes the symmetric difference quotient can yield an even better approximation than the regular difference quotient) On the calculator, press MATH and then #8, often referred to as “MATH 8” Algebraically, let h =. 001 (in most cases, . 001 is more than adequate)

EX: Computing a Numerical Derivative Compute NDER(x³, 2) by hand then use a calculator (the numerical derivative of x³ at x = 2) Algebraically, let h =. 001 (in most cases, . 001 is more than adequate)

• NDER is accurate up to 5 decimal places • There can be times when it incorrectly produces a result. EX 3: Failure of NDER Computer NDER(|x|, 0) (the numerical derivative |x| at x = 0)

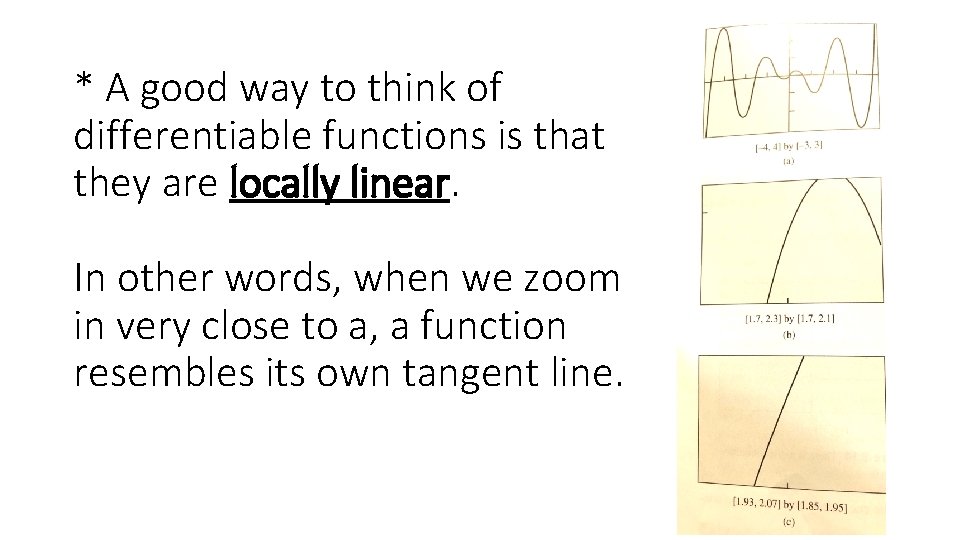
* A good way to think of differentiable functions is that they are locally linear. In other words, when we zoom in very close to a, a function resembles its own tangent line.

HW 3. 5 pg 146 QR #1 -7, EX 1 -31 odd, 24, 32, 34, 36

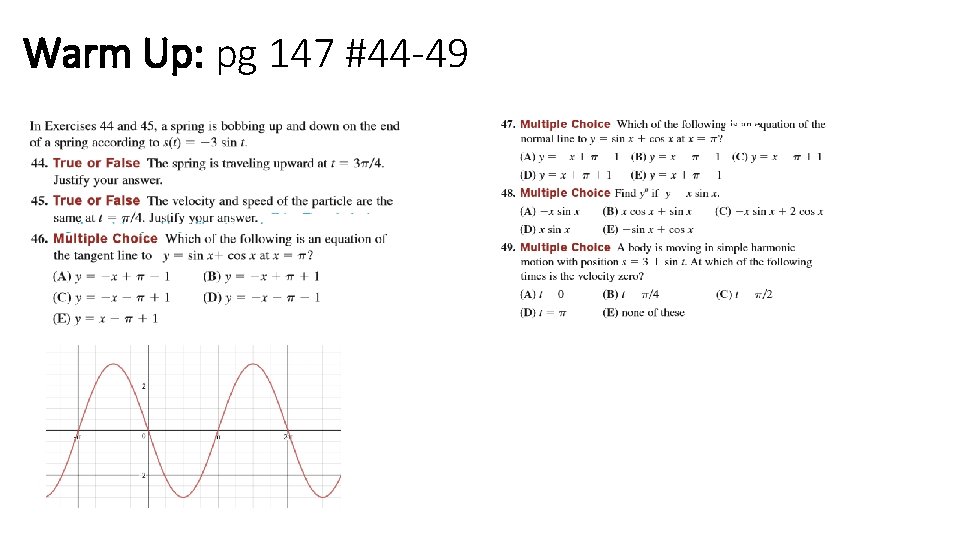
Warm Up: pg 147 #44 -49