Warm Up 1 Divide by using synthetic division

Warm Up 1. Divide by using synthetic division. 33 3 2 2 (8 x + 6 x + 7) ÷ (x + 2) 8 x – 10 x + 20 – x + 2 2. Divide by using synthetic division. 3 2 (x 3 – 3 x + 5) ÷ (x + 2) x – 2 x + 1 + x + 2 3. Use synthetic substitution to evaluate 194; – 4 3 2 P(x) = x + 3 x – 6 for x = 5 and x = – 1.

Learning Target I can: Use the Factor Theorem to determine factors of a polynomial. Factor the sum and difference of two cubes.

Recall that if a number is divided by any of its factors, the remainder is 0. Likewise, if a polynomial is divided by any of its factors, the remainder is 0. The Remainder Theorem states that if a polynomial is divided by (x – a), the remainder is the value of the function at a. So, if (x – a) is a factor of P(x), then P(a) = 0.

Example 1: Determining Whether a Linear Binomial is a Factor Determine whether the given binomial is a factor of the polynomial P(x). A. (x + 1); (x 2 – 3 x + 1) Find P(– 1) by synthetic substitution. – 1 1 – 3 1 1 – 4 4 5 P(– 1) = 5 P(– 1) ≠ 0, so (x + 1) is not a factor of P(x) = x 2 – 3 x + 1. B. (x + 2); (3 x 4 + 6 x 3 – 5 x – 10) Find P(– 2) by synthetic substitution. – 2 3 6 0 – 5 – 10 – 6 0 3 0 0 0 – 5 10 0 P(– 2) = 0, so (x + 2) is a factor of P(x) = 3 x 4 + 6 x 3 – 5 x – 10.

Check It Out! Example 1 Determine whether the given binomial is a factor of the polynomial P(x). a. (x + 2); (4 x 2 – 2 x + 5) Find P(– 2) by synthetic substitution. – 2 4 – 2 5 4 – 8 20 – 10 25 P(– 2) = 25 P(– 2) ≠ 0, so (x + 2) is not a factor of P(x) = 4 x 2 – 2 x + 5. b. (3 x – 6); (3 x 4 – 6 x 3 + 6 x 2 + 3 x – 30) Divide the polynomial by 3, then find P(2) by synthetic substitution. 2 1 – 2 2 1 – 10 1 2 0 4 0 2 5 10 0 P(2) = 0, so (3 x – 6) is a factor of P(x) = 3 x 4 – 6 x 3 + 6 x 2 + 3 x – 30.

Example 2: Factoring by Grouping Factor: x 3 – x 2 – 25 x + 25. (x 3 – x 2) + (– 25 x + 25) x 2(x – 1) – 25(x – 1) Group terms. Factor common monomials from each group. (x – 1)(x 2 – 25) Factor out the common binomial (x – 1)(x – 5)(x + 5) Factor the difference of squares.

Check It Out! Example 2 a Factor: x 3 – 2 x 2 – 9 x + 18. (x 3 – 2 x 2) + (– 9 x + 18) x 2(x – 2) – 9(x – 2) Group terms. Factor common monomials from each group. (x – 2)(x 2 – 9) Factor out the common binomial (x – 2)(x – 3)(x + 3) Factor the difference of squares.

Just as there is a special rule for factoring the difference of two squares, there are special rules for factoring the sum or difference of two cubes.

Example 3 A: Factoring the Sum or Difference of Two Cubes Factor the expression. 4 x 4 + 108 x 4 x(x 3 + 27) Factor out the GCF, 4 x. 4 x(x 3 + 33) Rewrite as the sum of cubes. 4 x(x + 3)(x 2 –x 3+ 3 2) 4 x(x + 3)(x 2 – 3 x + 9) Use the rule a 3 + b 3 = (a + b) (a 2 – ab + b 2).

Example 3 B: Factoring the Sum or Difference of Two Cubes Factor the expression. 125 d 3 – 8 Rewrite as the difference of cubes. (5 d – 2)[(5 d)2 + 5 d 2 + 22] Use the rule a 3 – b 3 = (a – b) (a 2 + ab + b 2). (5 d)3 – 23 (5 d – 2)(25 d 2 + 10 d + 4)

Check It Out! Example 3 b Factor the expression. 2 x 5 – 16 x 2 2 x 2(x 3 – 8) Factor out the GCF, 2 x 2. Rewrite as the difference of cubes. 2 x 2(x 3 – 23) 2 x 2(x – 2)(x 2 +x 2+ 2 2) 2 x 2(x – 2)(x 2 + 2 x + 4) Use the rule a 3 – b 3 = (a – b) (a 2 + ab + b 2).

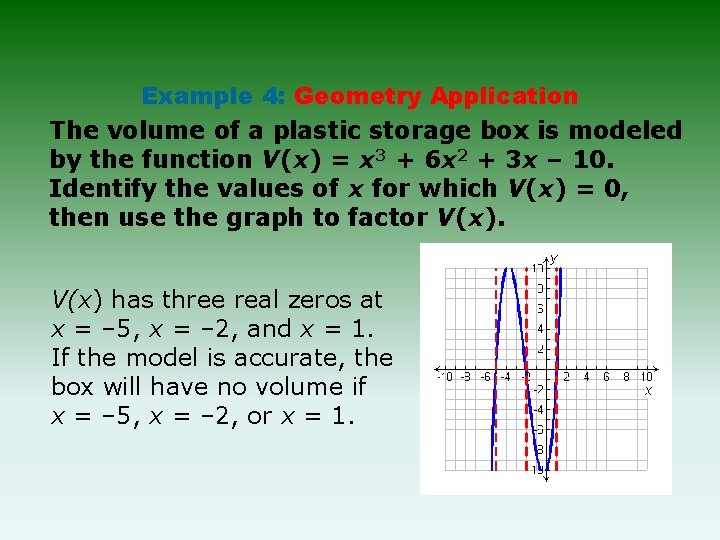
Example 4: Geometry Application The volume of a plastic storage box is modeled by the function V(x) = x 3 + 6 x 2 + 3 x – 10. Identify the values of x for which V(x) = 0, then use the graph to factor V(x) has three real zeros at x = – 5, x = – 2, and x = 1. If the model is accurate, the box will have no volume if x = – 5, x = – 2, or x = 1.

Example 4 Continued One corresponding factor is (x – 1). 1 1 6 3 – 10 1 7 10 0 Use synthetic division to factor the polynomial. V(x)= (x – 1)(x 2 + 7 x + 10) Write V(x) as a product. V(x)= (x – 1)(x + 2)(x + 5) Factor the quadratic.

Lesson Quiz 1. x – 1; P(x) = 3 x 2 – 2 x + 5 P(1) ≠ 0, so x – 1 is not a factor of P(x). 2. x + 2; P(x) = x 3 + 2 x 2 – x – 2 P(2) = 0, so x + 2 is a factor of P(x). 3. x 3 + 3 x 2 – 9 x – 27 (x + 3)(x – 3) 4. x 3 + 3 x 2 – 28 x – 60 (x + 6)(x – 5)(x + 2) 4. 64 p 3 – 8 q 3 8(2 p – q)(4 p 2 + 2 pq + q 2)