Walsh Functions A Gentle Introduction sources Complex Systems
























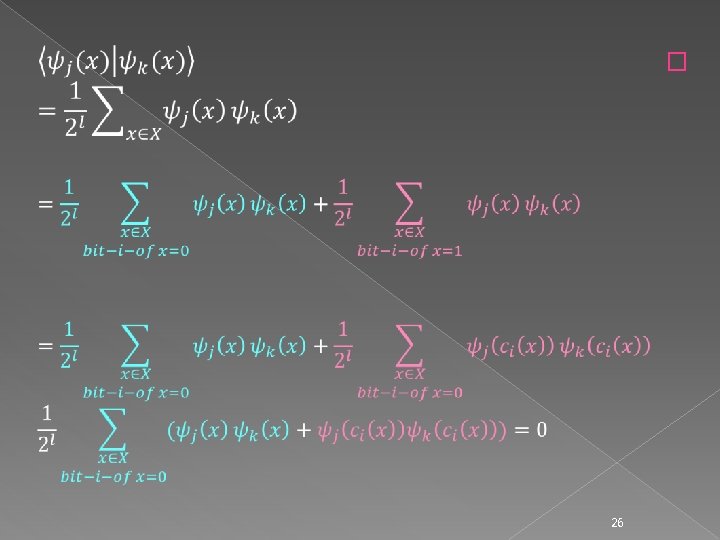




























- Slides: 60

Walsh Functions “A Gentle Introduction”

sources � Complex Systems › chapter 3: “GA and Walsh Functions Part-I A Gentle introduction”, › David E. Goldberg, › 1989, pages 129 -152. › Dept of Engineering Mechanics, Univ of Alabama, USA. � A Primer on Bethke’s Walsh schema transform › William A. Green › CSD Univ of New-Orleans, USA. 2

Outline of Discussion § § § Part I: An algebraic introduction. ← Part II: Overview of the Walsh Transform Part III: Walsh Analysis of Fitness Part IV: Walsh Coefficients Part V: Sumation 3

An algebraic introduction § § § Vector spaces The v. s. of functions Basis of a vector space The Inner product of a v. s Orthonormal Basis. 4

A Vector space � 5

Vector space F : a field Its elements called scalars V : a group Its elements called vectors 6

Basis of a of Finitely Generated Vector space. � 7

A Basis in a Vector space V : a group Of vectors … F : a field of scalars … 8

The v. s of functions � 9

The v. s of functions … R : the field of reals … 10

The Basis for vs F(x) � 11

Fitness function – linear combination 0 1 2 3 4 5 6 7 � 12

Inner product on a VS � 13

The inner product of vs F(X) � 14

Orthonormal basis � 15

An algebraic introduction § § § Vector spaces The v. s. of functions Basis of a vector space The Inner product of a v. s Orthonormal Basis. 16

Outline of Discussion § § § Part I: An algebraic introduction. Part II: Overview the Walsh Transform ← Part III: Walsh Analysis of Fitness Part IV: Walsh Coefficients Part V: Sumation 17

Motivation for finding an Orthonormal basis for F(X) 0 1 2 3 4 5 6 7 � 18

Walsh functions � 19


How Walsh functions are formed � 21

Finally… Walsh Function � 0 1 1 1 2 3 4 5 6 7 22

An algebric reminder…. � 23


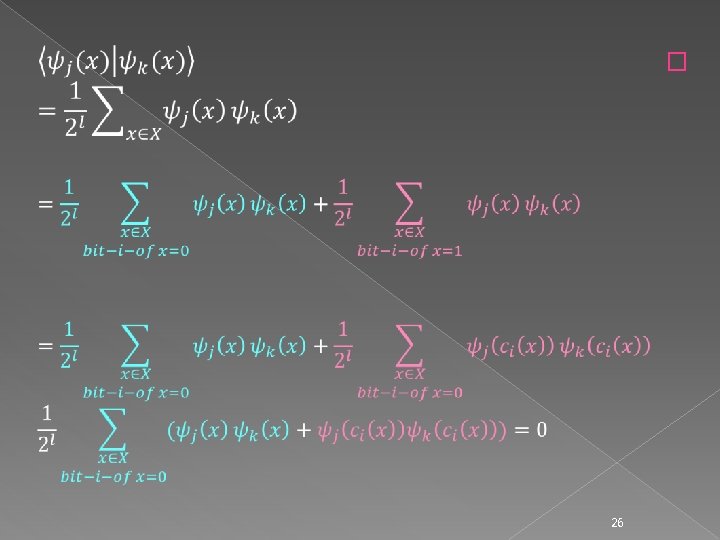

Walsh and Fitness func … … R : the field of reals 27

Walsh func, Walsh polynomials � 28

Walsh and Fitness func … R : the field of reals � 29

Outline of Discussion § § § Part I: An algebraic introduction. Part II: Overview of the Walsh Transform Part III: Walsh Analysis of Fitness ← Part IV: Walsh Coefficients Part V: Sumation 30

RELATED TERMS • • • Hadamard Martix Before we go on… A related term. square martix entries are either +1 or − 1 rows are mutually ortogonal geometric interpretation: this means that each pair of rows represent two perpendicular vectors Combinatorical interpretaion: it means that each pair of rows has matching entries in exactly half of their columns and mismatched entries in the remaining entries 31

Checkered Cat time #1 32

Outline of Discussion § § § Part I: An algebraic introduction. Part II: Overview of the Walsh Transform Part III: Walsh Analysis of Fitness ← Part IV: Walsh Coefficients Part V: Sumation 33

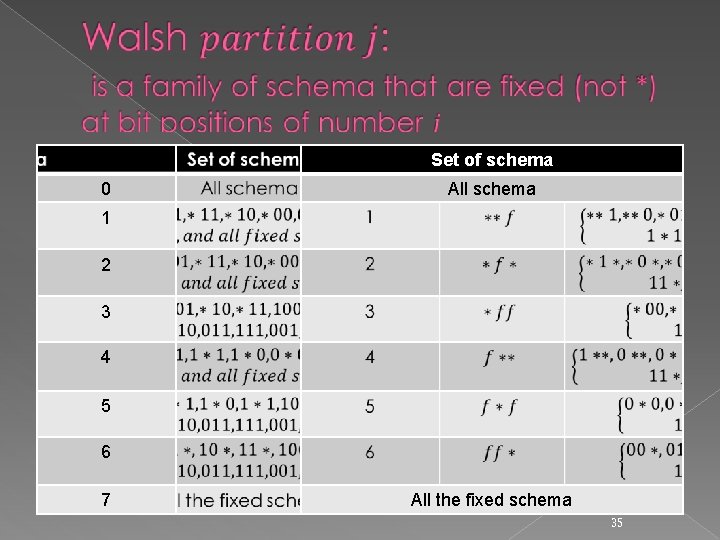
Schema: 0 1 � 2 3 4 5 6 7 34

Set of schema 0 All schema 1 2 3 4 5 6 7 All the fixed schema 35

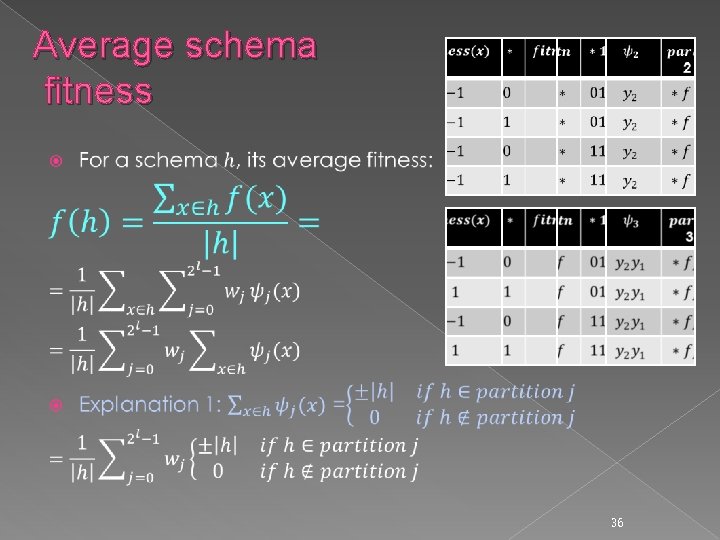
Average schema fitness � 36


Set of schema 1 1 � 38

Explanation 1: part 2 � 39


Some examples � 41

Walsh Schema Transform � 42

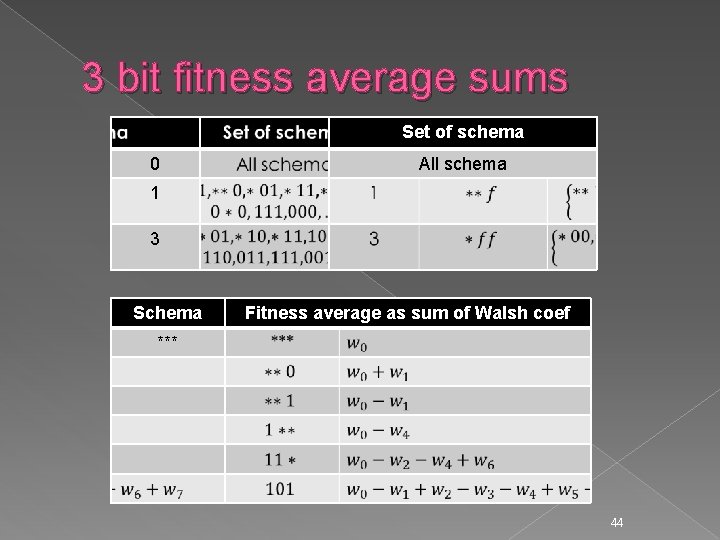
Calculating schema av sum � 43

3 bit fitness average sums Set of schema 0 All schema 1 3 Schema Fitness average as sum of Walsh coef *** 44

Outline of Discussion § § § Part I: An algebraic introduction. Part II: Overview of the Walsh Transform Part III: Walsh Analysis of Fitness Part IV: Walsh Coefficients ← Part V: Sumation 45

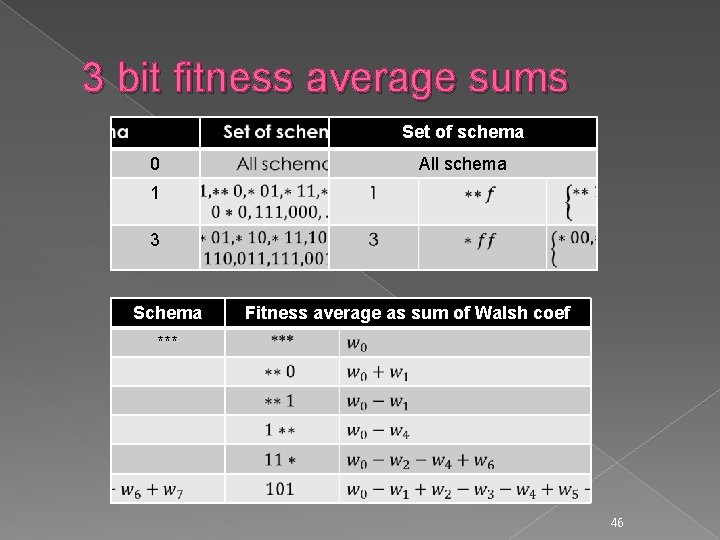
3 bit fitness average sums Set of schema 0 All schema 1 3 Schema Fitness average as sum of Walsh coef *** 46

Meaning of Walsh coefficients Schema Fitness average as sum of Walsh coef *** **0 **1 1** 11* 101 � Low order schema have few terms � High order schema have many terms 47


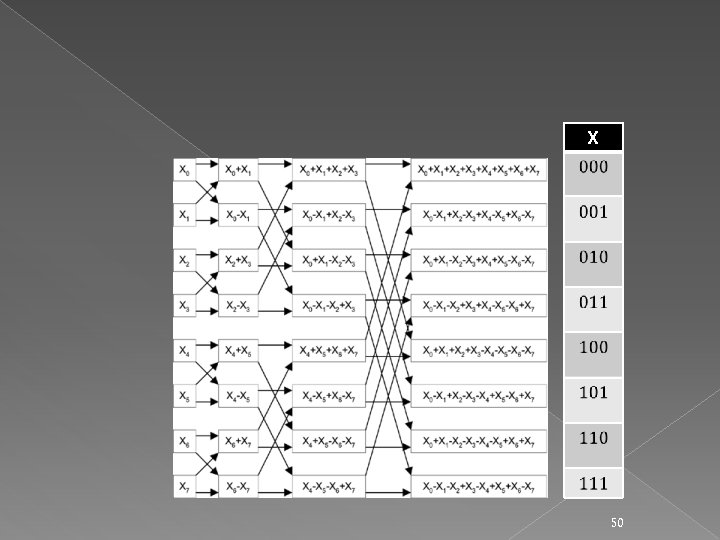
Walsh fast transform � Schema Fitness average as sum of Walsh coef 49

X 50

Cat time…. . 2# 51

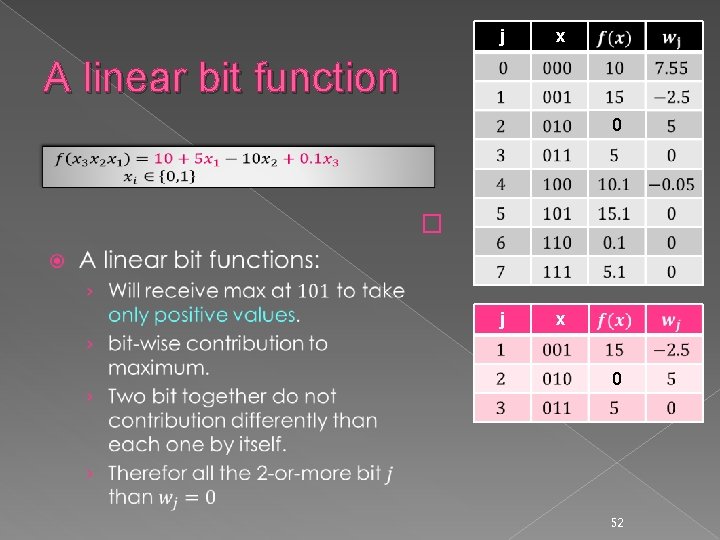
j x A linear bit function 0 � j x 0 52

Outline of Discussion Part I: An algebraic introduction. § Part II: Overview of the Walsh Transform § Part III: Walsh Analysis of Fitness § Part IV: Walsh Coefficients § § Part V: Sumation ← 53

sumation � Schema Fitness average as sum of Walsh coef *** 11* 101 54

FIN 55

j x A simple non linear f 4 � j x 4 56

Deception � Order of schema Schema 0 1 2 57

Deception � 58

Building blocks � Building-blocks: a component that fits with others to form a w hole. � The Walsh coeff fit with the intuitive understanding of building blocks. � That higher schema are built from their lower order schema. 59

How Walsh Func are formed: definitions � 60